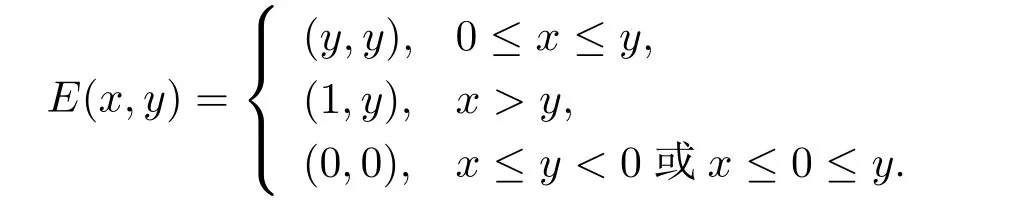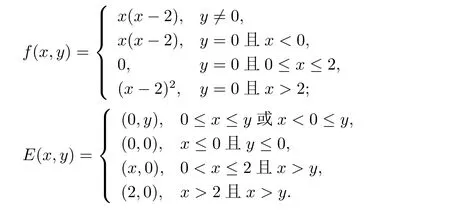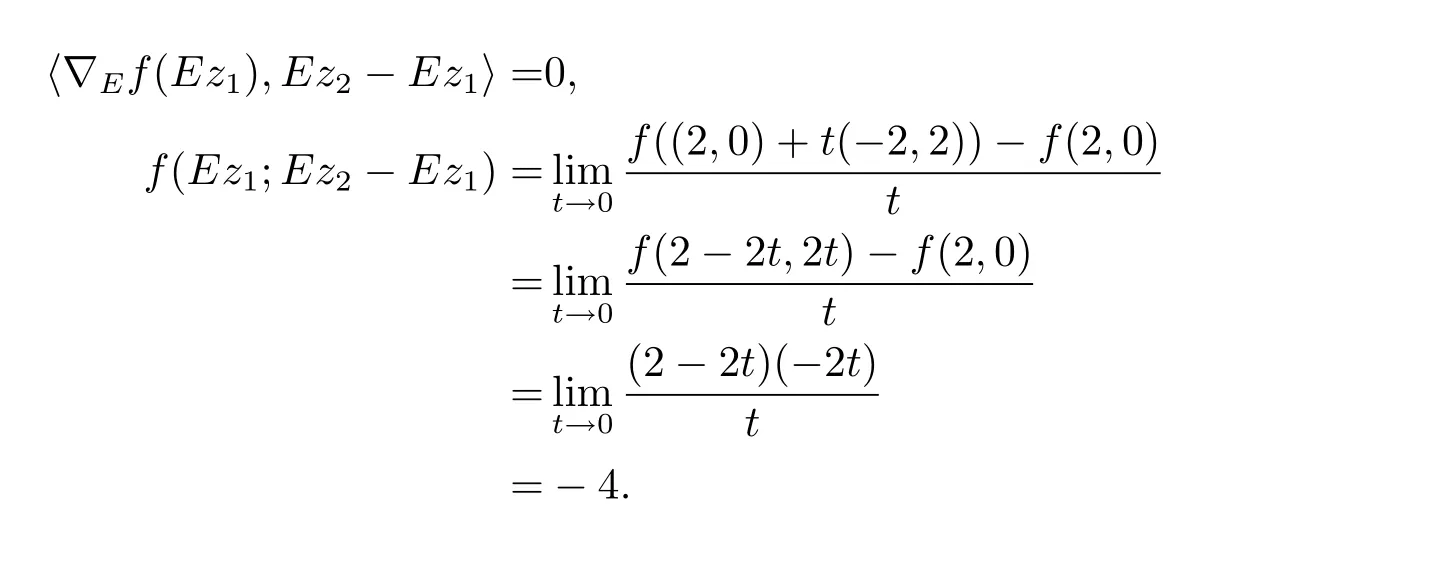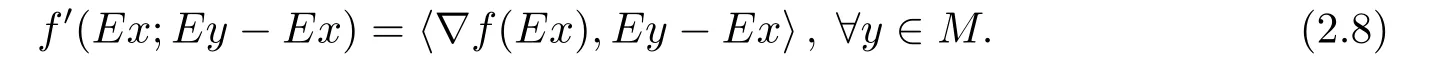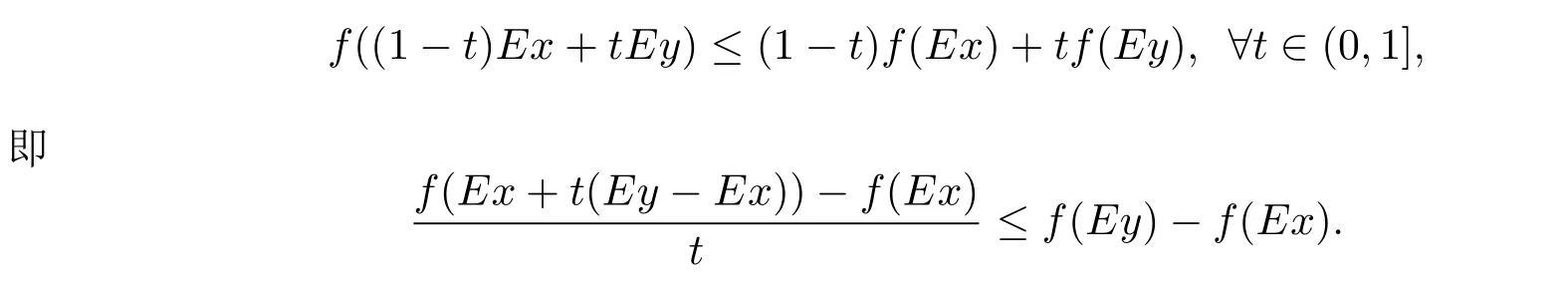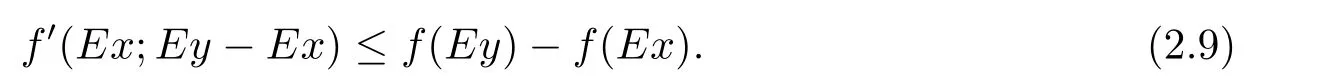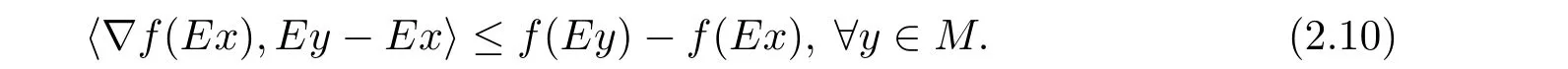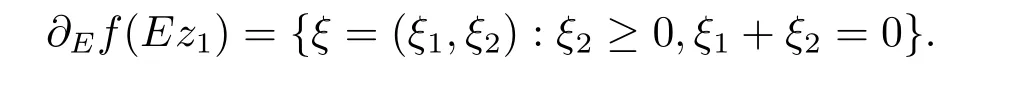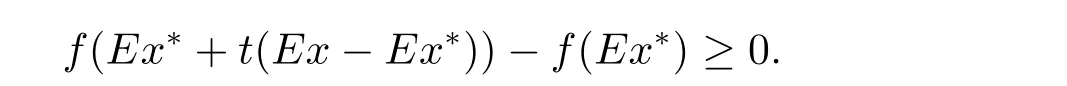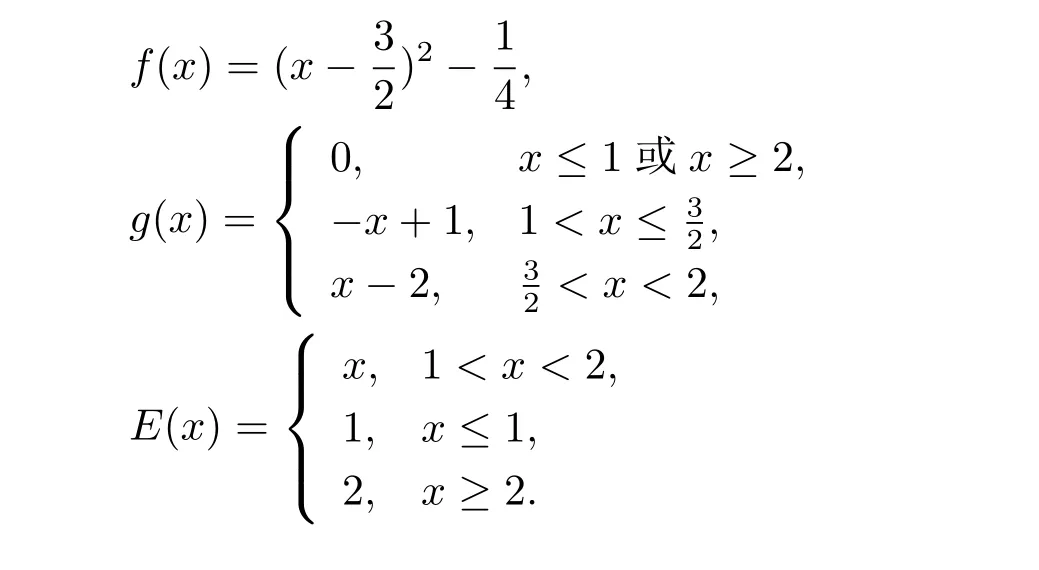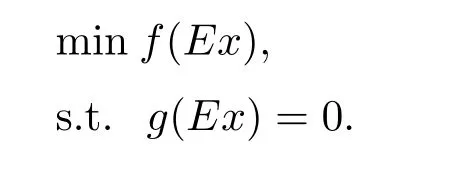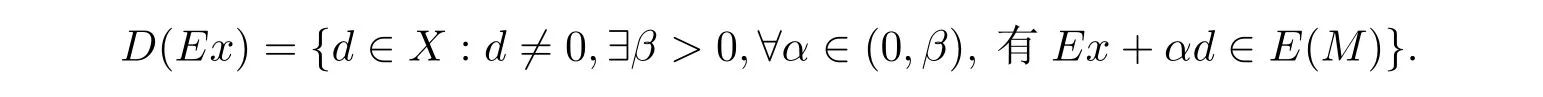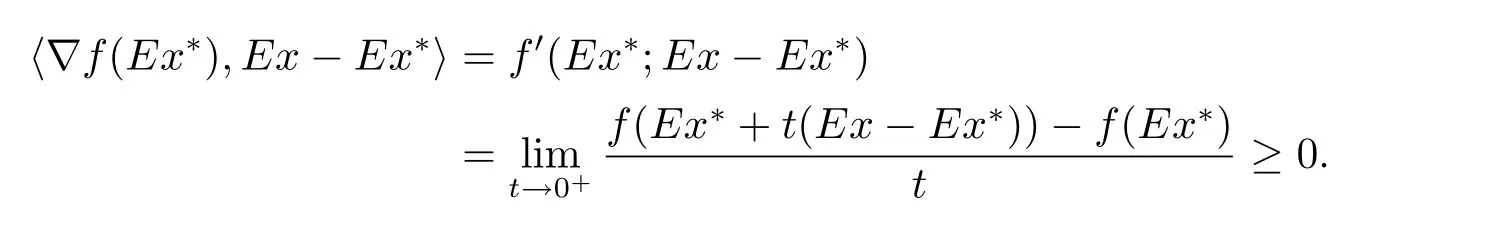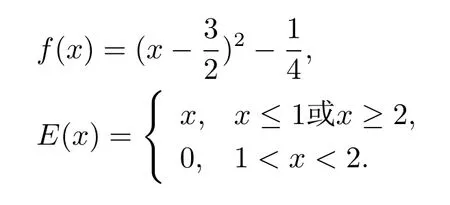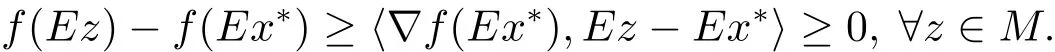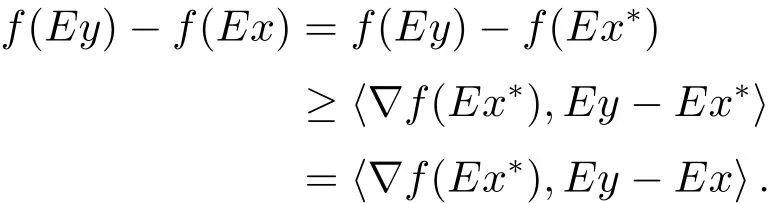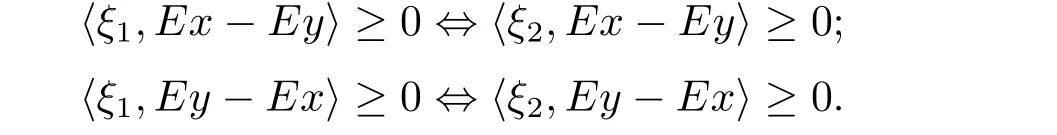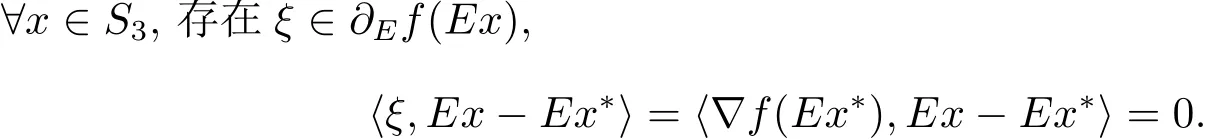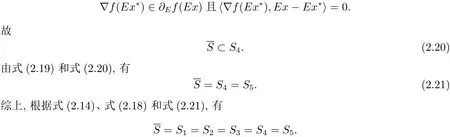Gateaux可微條件下E-凸規(guī)劃問題的解集刻畫

李 均,彭建文,劉學文

(重慶師范大學數(shù)學科學學院,重慶 401331)

1 引言

凸性條件無論是在數(shù)學還是經濟、工程以及管理科學等領域,都起著至關重要的作用.然而現(xiàn)實生活中大部分的實際問題卻難以滿足凸性假設,因此廣義凸性的研究就顯得尤為必要.1999年,Youness在文獻[1]中給出了如下的E-凸集、E-凸函數(shù)的概念.

定義1.1[1]稱M ?X 為E-凸集,如果存在映射E:X →X,?t∈[0,1]滿足

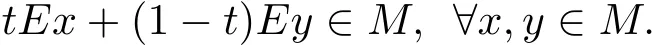
定義1.2[1]稱f:X→R為集合M?X上的E-凸函數(shù),如果存在映射E:X→X,使得M 為E-凸集,且?t∈[0,1]有

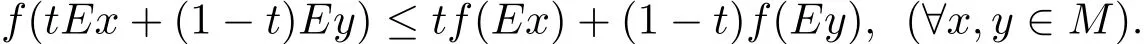
注1.1如果沒有特別說明,本文假設X 代表賦范線性空間,X?為其對偶空間,集合M ?X 均為開集.為了寫作方便,本文中將E(x)都簡寫為Ex.當E=I(單位映射)時,定義1.1、定義1.2分別退化為文獻[2]中凸集、凸函數(shù)的定義.

Youness在文獻[1]中對E-凸函數(shù)性質進行了初步探索,Yang[3]和Chen[4]舉例說明了文獻[1]中定理4.2、定理4.3、定理4.6是錯誤的.最近,Youness在文獻[5]中研究了如下帶不等式約束的E-凸規(guī)劃數(shù)學模型,簡記為(COP)E:

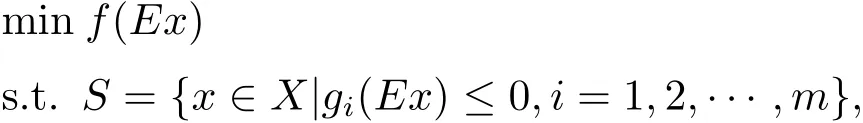
其中f,gi:X →R(i=1,2,···,m)都是X 上的E-凸函數(shù).

在文獻[5]中,Youness給出了多目標E-凸規(guī)劃問題有效解的性質刻畫.眾所周知,在凸優(yōu)化問題的研究中,次微分是一種重要的研究工具,Rockafellar在文獻[6]中給出了凸函數(shù)次梯度的定義.

定義1.3[6]稱ξ∈X?為凸函數(shù)f:X→R在x∈X 處的次梯度,如果

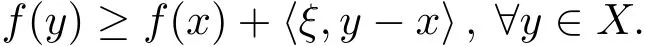
f在x處的次梯度的全體稱為f在x處的次微分,記為?f(x).

注1.2根據(jù)定義1.3,對任意y∈X,顯然有

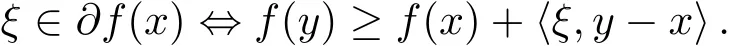
李成林等人在文獻[7]中,利用Clarke的思想給出了E-凸函數(shù)E-次微分的定義及其等價刻畫.

定義1.4[7]若M 是X中的E-凸集,f:M→R且x∈M∩dom(f),稱ξ∈X?是f在Ex處的E-次梯度,如果存在ε>0,η>0,使得?Ey∈B(Ex,η)?M,有

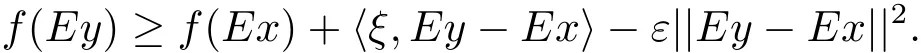
f在Ex處的E-次梯度的全體稱為f在Ex處的E-次微分,記為?Ef(Ex).

定理1.1[7]若f是E-凸集M ?X 上的E-凸函數(shù),則?x,y∈M,有

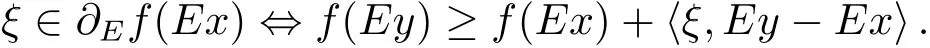
史樹中在文獻[2]中給出了函數(shù)的左、右方向導數(shù)及Gateaux可微的定義.

定義1.5[2]f:X→R是實值函數(shù),x∈X,d∈X,

定義1.6[2]設f:X→R是實值函數(shù),x∈X,若f0(x;d)對任意方向d都存在,且存在δ∈X?使得f0(x;d)=hδ,di,?d∈X.那么稱f在x處Gateaux可微,并稱δ為f在x處的Gateaux導數(shù),記作δ=?f(x).

注1.3文獻[8]中給出了這樣的結論:若凸函數(shù)f:X→R在x∈X處Gateaux可微,則有?f(x)={?f(x)}.

姜艮等人在文獻[9]中給出了E-Gateaux可微的定義.

定義1.7[9]若M 是賦范線性空間X中的E-凸集,f:M →R是M 上的E-凸函數(shù)且x∈M ∩dom(f),稱f在Ex處E-Gateaux可微,若有δ∈X?,使得f0(Ex;d)=hδ,di,?d∈E(X).若f在Ex處E-Gateaux可微,并稱δ為f在Ex處的E-Gateaux導數(shù),記作δ=?Ef(Ex).

在文獻[9]中,姜艮等人得到了如下的結論.

定理1.2[9]若X是賦范線性空間,M 是X上的E-凸集,f:M→R是M 上的E-凸函數(shù)且x∈M ∩dom(f),如果f在Ex處E-Gateaux可微,則?Ef(Ex)={?Ef(Ex)}.

定理1.3[9]若x?是(COP)E的解,如果f在Ex?處E-Gateaux可微,則?x∈S,則有h?Ef(Ex?),Ex ? Ex?i≥ 0.

定理1.2和定理1.3是文獻[9]的基礎性定理,文獻[9]中的其他結論都是基于這兩個結論建立的,本文將舉例說明這兩個結論都是不正確的,并進一步研究如下的E-凸規(guī)劃問題

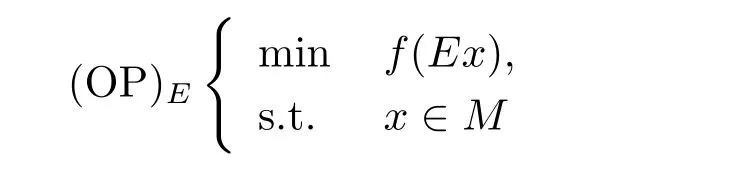
在Gateaux可微條件下最優(yōu)解集的性質定理及最優(yōu)解集等價刻畫,其中f:M →R是E-凸函數(shù).

2 主要內容

在定理1.2的證明中有

式(2.1)顯然是錯誤的,因為Ez只能取遍E(M),不一定能取遍全空間X.下面例2.1說明式(2.1)是錯誤的.

例2.1令X=R2,M={(x,y):0

函數(shù)f:X→R定義為f(x,y)=c(常數(shù)).容易驗證M 為E-凸集,f為M 上的E-凸函

情形1 當x≤ y時,則Ez=(y,y),設ξ=(ξ1,ξ2),由定理1.1,要使得ξ∈?Ef(Ez1),ξ必須滿足

情形2 當x>y時,則Ez=(1,y),設 ξ=(ξ1,ξ2),由定理1.1,要使得 ξ∈ ?Ef(Ez1),ξ必須滿足式(2.2),于是有

結合式(2.3)和式(2.4)可求得滿足式(2.2)的ξ必須滿足下面的條件:

又因為y∈(0,1),所以ξ∈?Ef(Ez1)必須滿足ξ2≥0且ξ1+ξ2=0.故

再計算?Ef(Ez1).根據(jù)定義1.7,設δ=(δ1,δ2),要使δ=?Ef(Ez1),必須滿足下面的條件:

即 0= δ1+δ2λ, ?λ ∈ R.所以 δ=(0,0),故

由式(2.5)和式(2.6)知{?Ef(Ez1)}6=?Ef(Ez1).

在定理1.2的證明中使用了如下語句

因為f在Ex處E-Gateaux可微=?f0(Ex;Ey?Ex)=h?Ef(Ex),Ey?Exi. (2.7)并由式(2.7)證得?Ef(Ex)∈?Ef(Ex),但是式(2.7)是錯誤的,其原因在于Ey?Ex∈E(X)一般不成立.下面例2.2說明式(2.7)是不正確的.

例 2.2 令X=R2,M={(x,y):?1

容易驗證M 為E凸集,f為M 上的E凸函數(shù),d=(2,0)或d=(0,λ),(λ∈R+)為E(X)中的任意方向.這里特別取z1=(2,1),則Ez1=(2,0),顯然可得f在Ez1處E-Gateaux可微且?Ef(Ez1)=(0,0).令z2=(1,2),則Ez2=(0,2),此時Ez2?Ez1=(?2,2)/∈E(X),而顯然f0(Ez1;Ez2?Ez1)6=h?Ef(Ez1),Ez2?E1i.

定理1.2可以被糾正為如下的結論.

定理2.1 X是賦范線性空間,M 是X上的E-凸集,f:M→R是M 上的E-凸函數(shù)且x∈M∩dom(f),如果f在Ex處Gateaux可微,則?f(Ex)∈?Ef(Ex).

證 因為f在Ex處Gateaux可微,由定義1.6,則有

又因為f:M→R是M 上的E-凸函數(shù),則有

在上式中取t→0+,則有

于是由式(2.8)和式(2.9)知

由定理1.1,故?f(Ex)∈?Ef(Ex).

注2.1 若f在Ex處Gateaux可微,?Ef(Ex)={?f(Ex)}不一定成立.在例2.1中,函數(shù)f在處Gateaux可微,且?f(Ez1)=(0,0),但是f在Ez1處的E-次微分是

在定理1.3的證明中存在:x?是(COP)E的解,則對t∈[0,1],有

該結論是不正確的,其原因是這里并未能保證Ex?+t(Ex?Ex?)∈E(S).下面的例2.2說明定理1.3是錯誤的.

例2.3 令X=R,函數(shù)f,g:X→R,映射E:X→X分別定義為

這里E-凸規(guī)劃問題(COP)E為

容易驗證函數(shù)f,g都是X 上的E-凸函數(shù),E(X)中的方向只有d=1,且可求得(COP)E問題可行域S={x∈R:x≤1或x≥2}.經驗證x=1或x=2為(COP)E問題的最優(yōu)解.這里特別取x?=2為(COP)E問題的一個最優(yōu)解,根據(jù)定義1.7可以求得?Ef(Ex?)=1.但是存在點x=1,則Ex=1,使得h?Ef(Ex?),Ex?Ex?i=1×(1?2)=?1<0.從而知定理1.3的結論不一定成立.

文獻[10]中介紹了可行方向錐的概念,這里給出E-可行方向錐的概念.

定義2.1集合M ?X 為E-凸集,x∈M,記Ex處的E-可行方向錐為

將定理1.3糾正為如下的定理.

定理2.2若x?是(OP)E的解,f在Ex?處Gateaux可微,且對x∈M,有Ex?Ex?∈D(Ex?),則 h?f(Ex?),Ex ?Ex?i≥ 0.

證 因為x?是(OP)E的解,Ex?Ex?∈D(Ex?),則存在β>0,使得?t∈(0,β),有Ex?+t(Ex?Ex?)∈ E(M)且 f(Ex?+t(Ex?Ex?))?f(Ex?)≥ 0.又因為 f 在 Ex?處Gateaux可微,則有

即 h?f(Ex?),Ex?Ex?i≥ 0.

用下面的例子來說明定理2.2的合理性.

例2.4 這里取M=R,函數(shù)f與映射E分別定義如下

易知x=1或者x=2為(OP)E的最優(yōu)解,下面討論x?分別取1和2時的情況.

情形1 當x?=1時,則Ex?=1,f在Ex?=1處Gateaux可微且?f(Ex?)=?1,此時可求得f在Ex?處的可行方向錐為D(Ex?)={d∈X:d<0}.當x<2且x 6=1時,有Ex?Ex?∈ D(Ex?),因此 h?f(Ex?),Ex?Ex?i≥ 0.

情形 2 當x?=2時,則Ex?=2,f在Ex?=2處Gateaux可微且?f(Ex?)=1,此時可求得f在Ex?處的可行方向錐為D(Ex?)={d∈X:d>0}.當x>2時,有Ex?Ex?∈ D(Ex?),因此 h?f(Ex?),Ex?Ex?i≥ 0.

下面給出E-凸規(guī)劃問題(OP)E的一個性質定理.

定理2.3若f:M→R上E-凸函數(shù),S為(OP)E規(guī)劃的最優(yōu)解集,x?∈且滿足f在Ex?處Gateaux可微且?z∈M都有Ez?Ex?∈D(Ex?),則?f(Ex?)

證 因為f在Ex?處Gateaux可微,由定理2.1可得?f(Ex?)∈?Ef(Ex?).又由定理2.2,有

取 z=x,則 h?f(Ex?),Ex?Ex?i=0,由上式知,?y ∈ M,有

由定理1.1可得?f(Ex?)∈ ?Ef(Ex).因此?f(Ex?)

定理2.4若M是賦范線性空間X中的E-凸集,且f:M→R是M上的E-凸函數(shù),則(1)?(2)?(3)?(4)?(5),其中(1),(2),(3),(4),(5)的定義分別為

(1) 存在 ξ1∈ ?Ef(Ex),ξ2∈ ?Ef(Ey),滿足 hξ1,Ex?Eyi=0,hξ2,Ex?Eyi=0;

(2) 存在 ξ1∈ ?Ef(Ex),ξ2∈ ?Ef(Ey),滿足 hξ1? ξ2,Ex?Eyi≤ 0;

(3) ?Ef(Ex)∩ ?Ef(Ey)6= φ;

(4) 存在 ξ1∈ ?Ef(Ex),ξ2∈ ?Ef(Ey),滿足

(5) 存在 ξ1∈ ?Ef(Ex),ξ2∈ ?Ef(Ey),滿足

進一步,若x,y是(OP)E的解,f在點Ex,Ey處Gateaux可微且Ex?Ey∈D(Ey),Ey?Ex∈D(Ex),則(5)?(1).

證 (1)? (2)? (3)? (4)可以參見文獻[9]的定理2.3,這里(4)? (5)直接取d=Ex?Ey即可.下證(5)?(1).

因為f在Ex,Ey處Gateaux可微且Ex?Ey∈D(Ey),Ey?Ex∈D(Ex),根據(jù)定理2.2有

又因為x,y是(OP)E的解,再由定理1.1和定理2.1,則

由式(2.11)–(2.13)可知,這里取ξ1=?f(Ex),ξ2=?f(Ey)即滿足(1).

最后給出E-凸規(guī)劃問題(OP)E最優(yōu)解集的幾種等價刻畫.

證 首先證明S3=S4=S5.根據(jù)定義,S3?S4?S5顯然成立.

下證S5? S3,若x∈S5,存在ξ∈?Ef(Ex)使得hξ,Ex?Ex?i≤ 0由定理1.1,定理2.1和定理2.2,有

對任意的y∈M,由定理1.1及定理2.1可得

再根據(jù)定理1.1有

故

由式 (2.15)–(2.17),有

再證S5?S?S4.

設x∈S5,因為x?∈S,所以

又因為存在ξ∈?Ef(Ex)使得hξ,Ex?Ex?i≤0,由定理1.1有

設x∈S,由定理2.3的證明可知