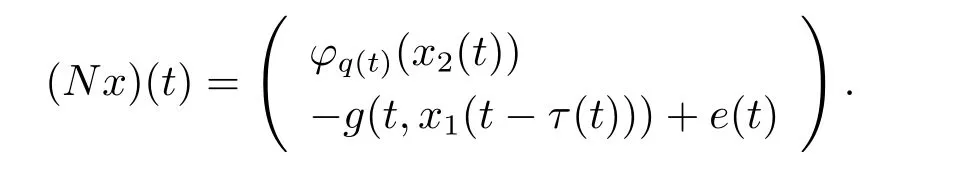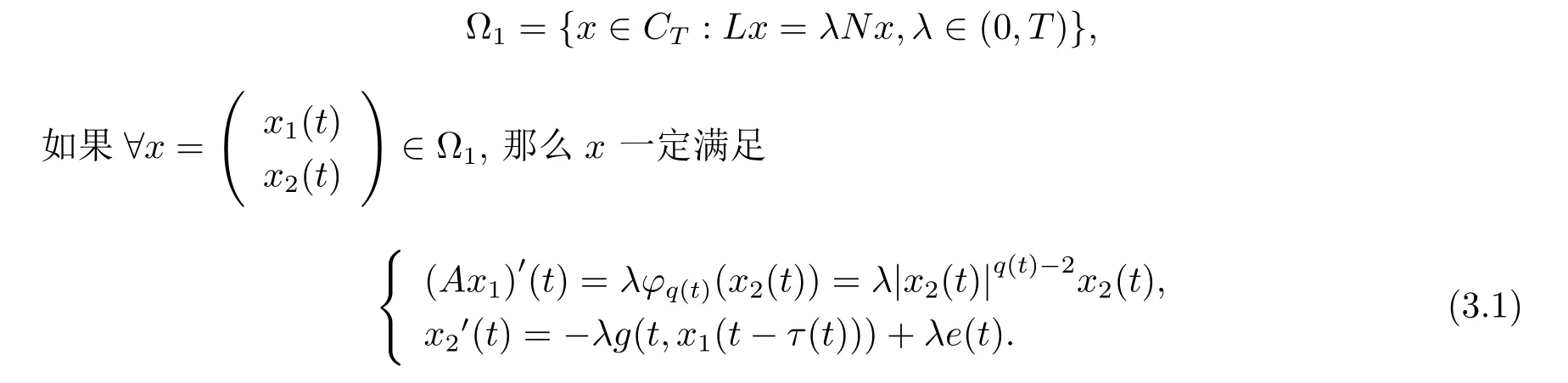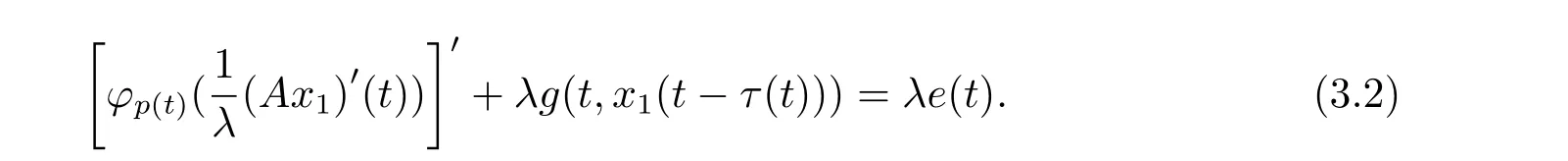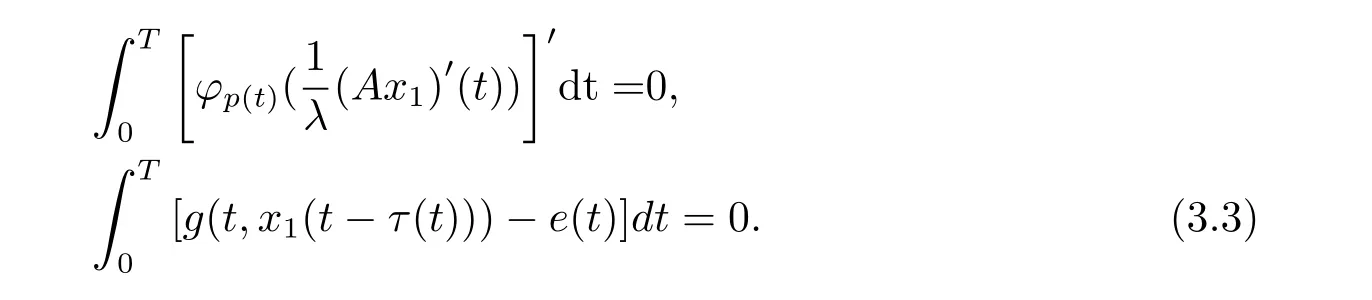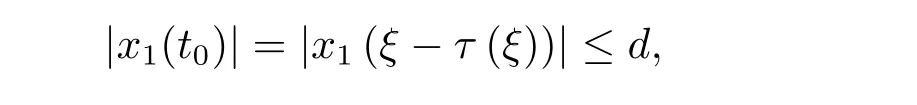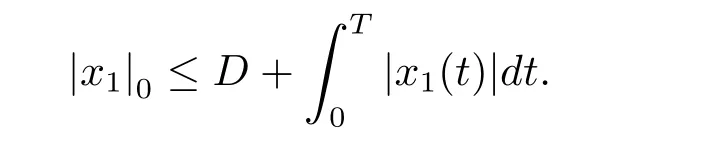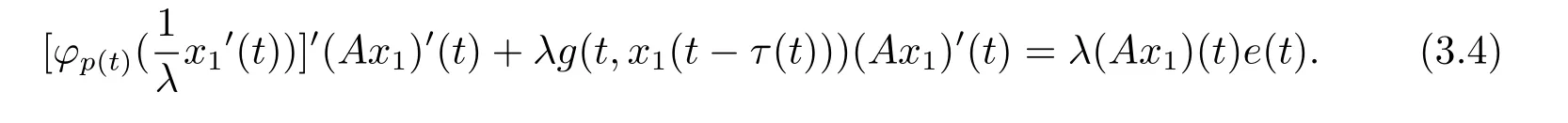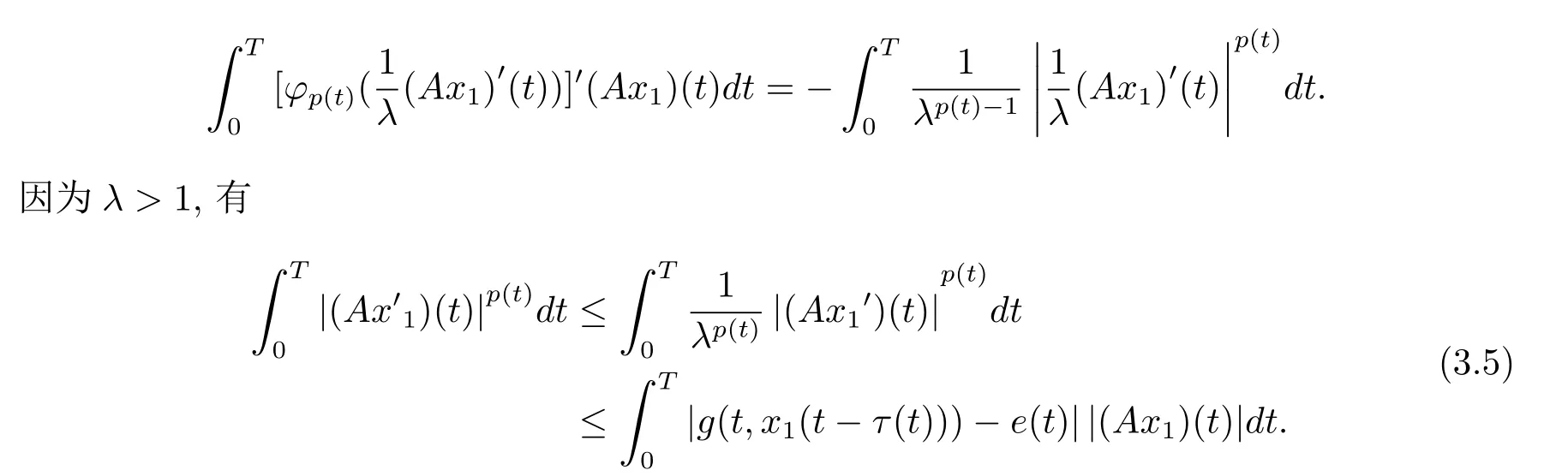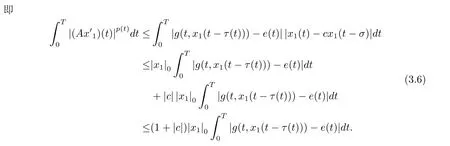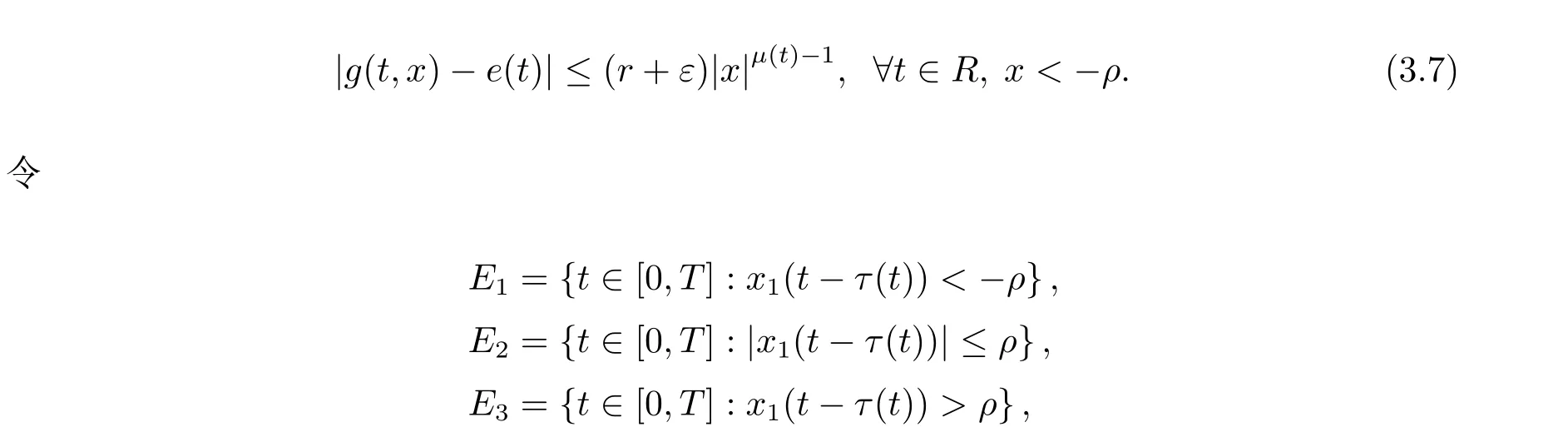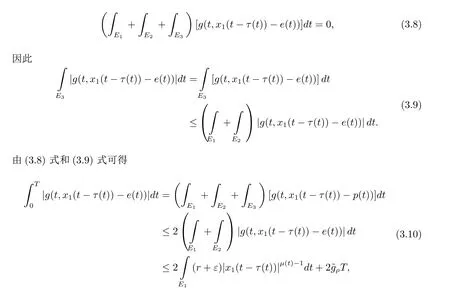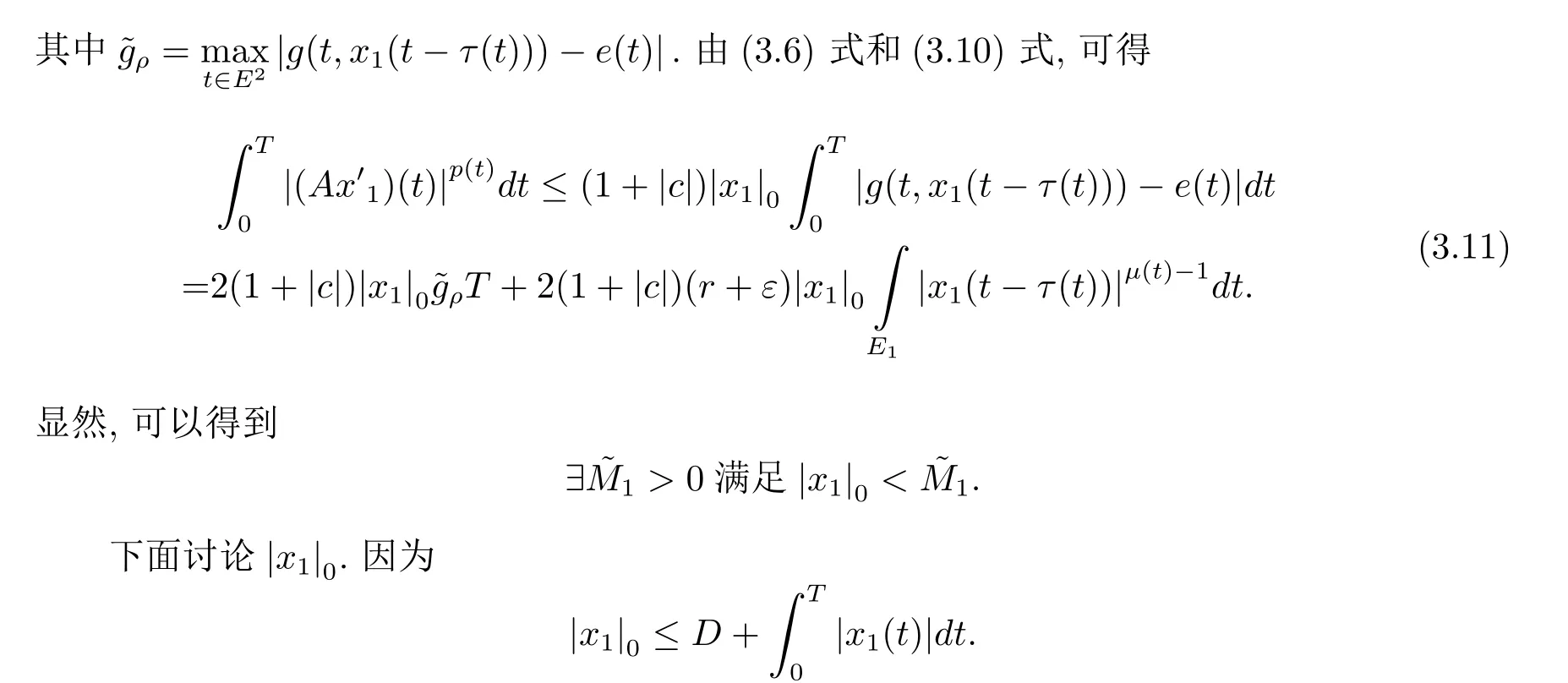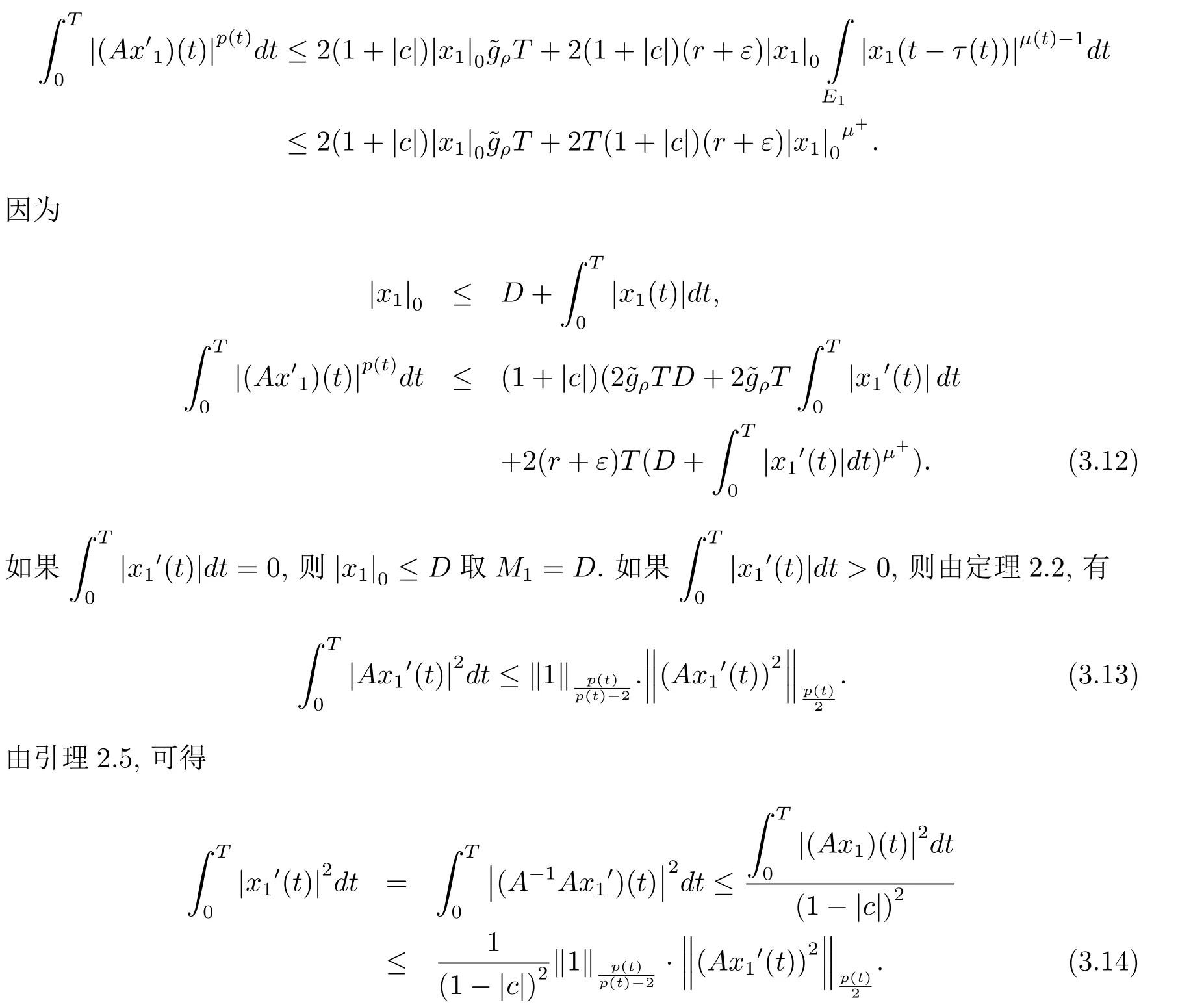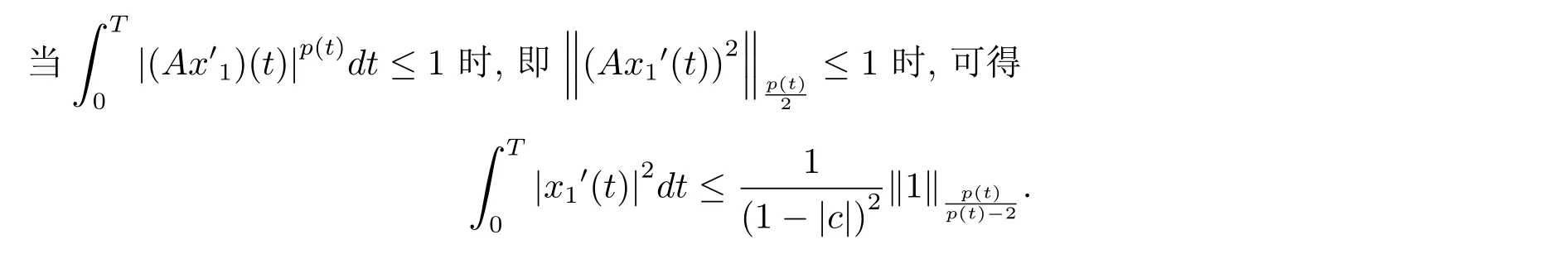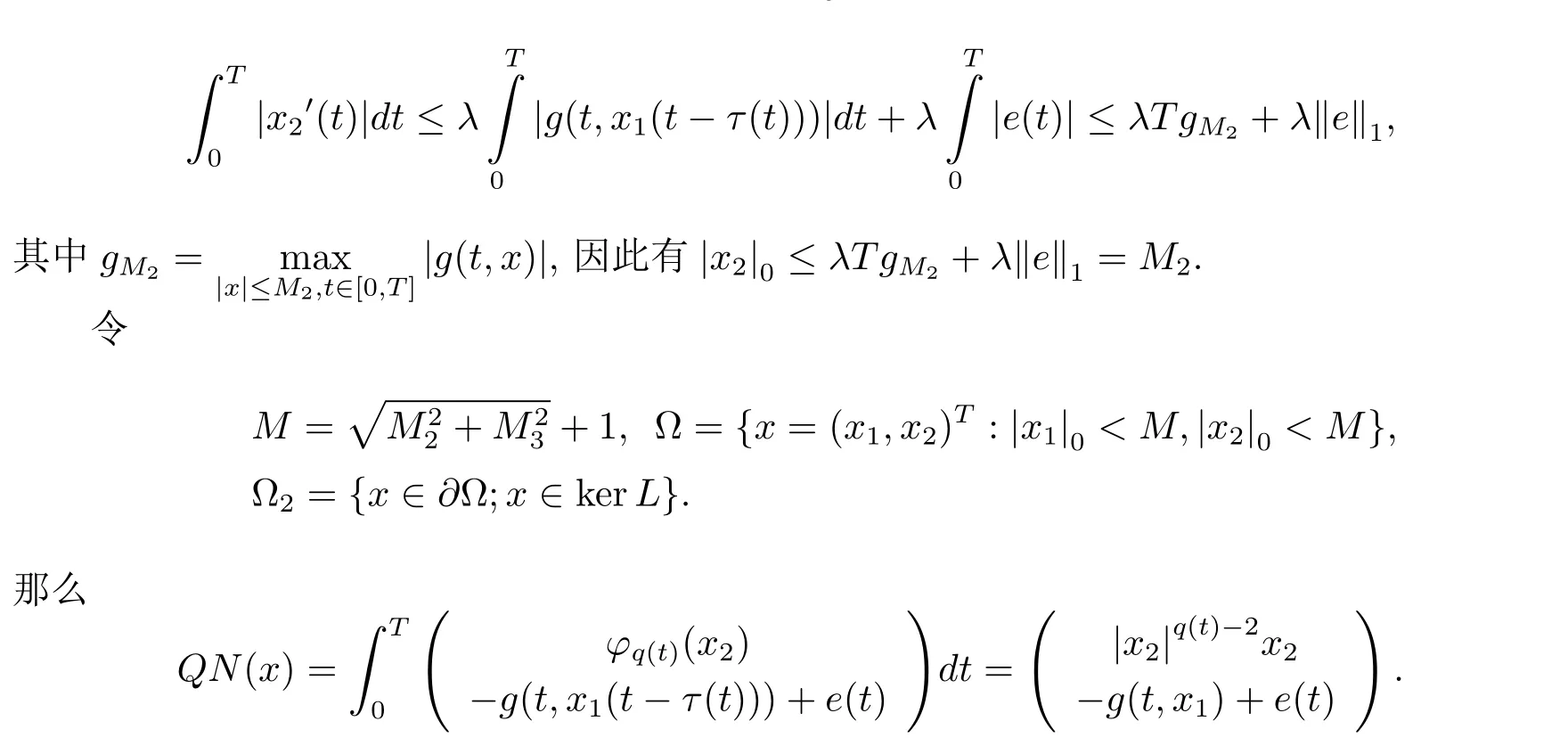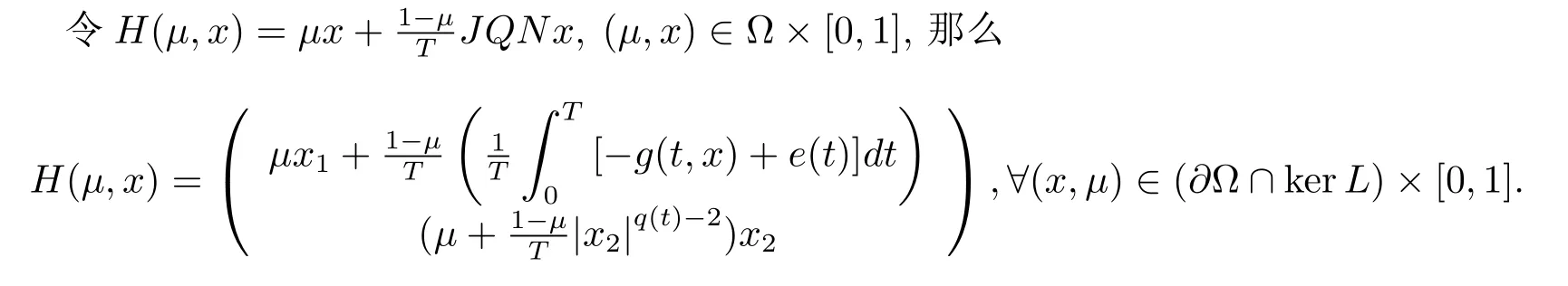求一類p(t)-Laplace中立型微分泛函方程解的存在性
于 美,馬國禎
(西北工業大學理學院,陜西西安 710072)
1 引言
近年來,隨著自然科學和工程技術中許多非線性問題的不斷出現,Sobolev空間表現出了其應用范圍的局限性.例如,對一類有變指數增長條件的非線性問題的研究.具有變指數增長性條件的非線性問題是一個新興的研究課題.在對這類非線性問題進行研究時,變指數Lebesgue空間及Sobolev空間發揮著重要的作用[1?4].
在本文中,我們主要研究一類p(t)-Laplace中立型微分泛函方程
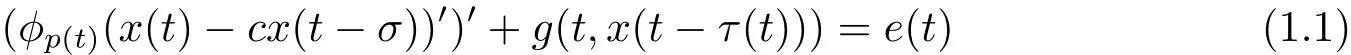
周期解的存在性,其中 φp(t):R → R,φp(t)(u)=|u|p(t)?2u,g∈C(R2,R),1 由于指數p(t)為函數,p(t)-Laplace算子較之p-Laplace具有更復雜的非線性性,許多對于p-Laplace問題成立的方法和結果不再適用于p(t)-Laplace問題.本文結合了Mawhin連續定理與不等式技巧的應用,克服了變指數p(t)產生的困難,得到了新的研究成果.關于常指數增長條件下的周期解存在性的問題,可參考文獻[5–6]. 首先回憶一些關于變指數Lebesgue空間Lp(t)(?)的定理[7]. 定義2.1設P是所有Lebesgue可測函數集,且p:?→(1,∞).對于p(t)∈P(?),設 變指數Lebesgue空間Lp(t)(?)是由一類滿足的函數u組成,且Lp(t)(?)是由上述范數誘導的Banach空間.定義p(t)∈P(?)的共軛函數q(t)為q(t)= 定理2.2令p∈P(?),那么 對于每個f∈Lp(t)(?)和g∈Lp0(t)(?)都成立. 定理2.3設u,uk∈Lp(t)(?),則 對于Mawhin連續性定理[8].令X,Y是實Banach空間,L:D(L)?X→Y是一個Fredholm算子并且指數為0,D(L)是L的值域,這意味著ImL在Y上是一個閉域并且有 考慮補充子空間X1,Y1,其中X=KerL⊕X1,Y=ImL⊕Y1.令P:X→KerL,Q:Y→Y1是自然投影.顯然有KerL∩(D(L)∩X1)={0}.因此限制條件LP:=L|D(L)∩X1是可逆的,由K表示LP的逆. 令?是X的一個開的有界子集并且D(L)∩? 6=φ.如果QN(ˉ?)是有界的,算子K(I?Q)N:ˉ?→X是致密的,則在ˉ?中N:ˉ?→Y是L-緊致的. 引理2.4假設X,Y是兩個Banach空間,L:D(L)?X→Y是一個Fredholm算子并且指數為0.此外??X是一個開的有界集合,在ˉ?上N:ˉ?→Y是L-緊致的.如果有 (1)Lx 6= λNx,?x∈ ?? ∩D(L),λ ∈ (0,1). (2)Nx/∈ImL,?x∈??∩KerL. (3)deg{JQN,?∩KerL,0}6=0,其中J:ImQ→ KerL是同構的.則Lx=Nx在ˉ?∩D(L)上有一個解. 引理2.5如果|c|6=1,且A在CT上有連續有界映射,那么 首先把方程(1.1)寫成如下形式 假設T是一個大于0的常數CT={?:?∈C(R,R),?(t+T)≡?(t)}且具有范數|?|0=|?(t)|,X=Y ={x=(x1(t),x2(t))∈ C(R,R2):x(t+T)≡ x(t)} 具范數kxk=max{|x1|0,|x2|0},顯然X 和Y是Banach空間.令 所以L是一個指標為零的Fredholm算子. 令投影P:X→KerL與Q:Y→ImQ定義如下 給出以下假設條件 引理3.1如果p(t)>2且存在正常數D,r≥0滿足[H1]–[H2],則(1.1)至少有一個T型周期解. 證 顯然當且僅當Lx=Nx成立時,方程(P)有T型周期解,其中N:CT→CT, 由(3.1)式的第一個等式可得x2(t)=Ax1)0(t)),將其代入(3.1)式的第二個等式,可得 在區間[0,T]上積分(3.2)式的兩邊,由牛頓-萊布尼茲定理,可得 由積分中值定理,存在常數ξ∈[0,T]滿足g(ξ,x1(ξ?τ(ξ)))?e(t)=0.由假設[H1]可得|x1(ξ? τ(ξ))|≤ D.令 ξ? τ(ξ)=kT+t0,其中 k ∈ Z,t0∈ [0,T),因此 這意味著 另一方面,將(3.2)式兩端同時乘(Ax1)(t),可得 在區間[0,T]上積分(3.4)式的兩邊,由于 由假設[H2]可知,?ρ>0滿足 由(3.3)式可得 由于μ+<2可得,存在C>0,使得因此|x1|0≤ D+C+T=M1.綜上所述,?M1>0,使得|x1|0 下面討論|x2|0的邊界.由(3.1)式的第一個等式,可知這意味?t1∈[0,T]著滿足x2(t1)=0,因此dt.由(3.2)式的第二個等式可得 若QNx=0,那么x2=0,x1=M,或=M.但是當x1=M 時,顯然?g(t,x1)+e(t)<0矛盾.當x1=?M時,顯然QNx 6=0,?x∈?,x/∈ImL,因此引理2.4中(1)和(2)均得到滿足. 下面證明引理2.4(3)同樣成立.定義同構:J:ImQ→kerL:J(x1,x2)T=(x2,x1)T. 如果H(μ,x)=0,那么x2=M或?M.與上面的證明類似,也可證明H(μ,x)6=0.因此 因此引理2.4的以三個條件同樣成立.應用引理2.4,可得Lx=Nx在上有一個解幾乎處處成立,方程(1.1)存在一個周期解.2 預備知識
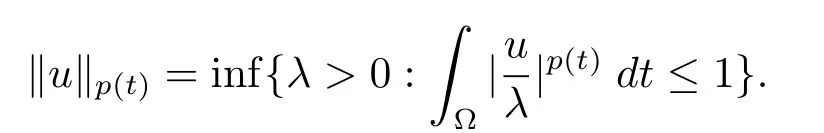
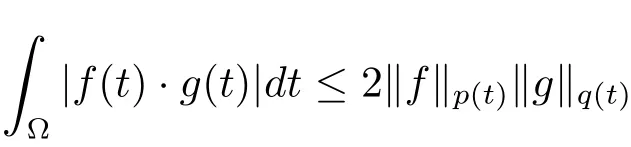

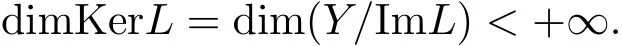
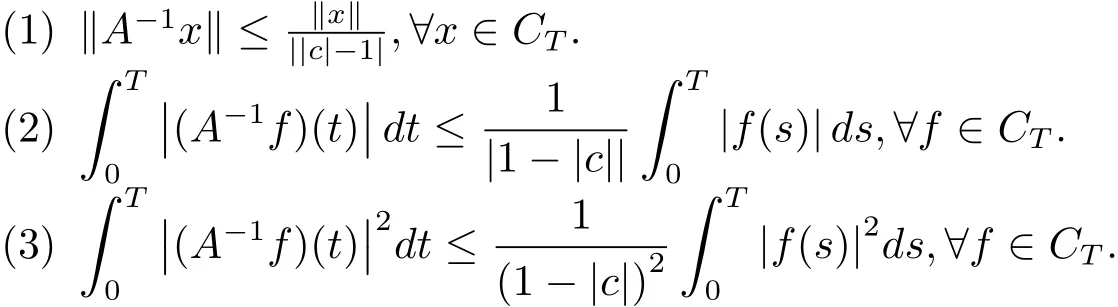
3 周期解的存在性
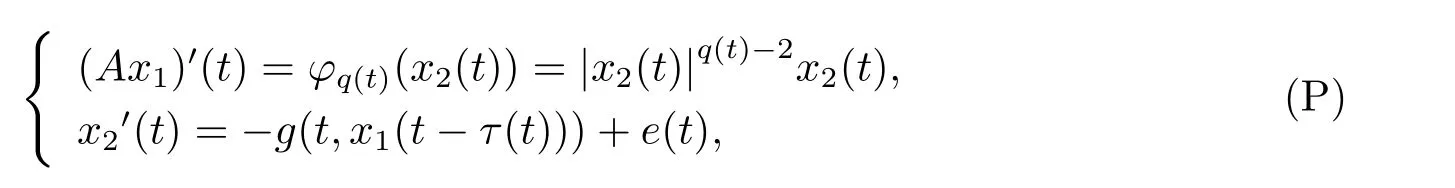
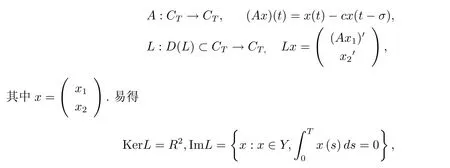
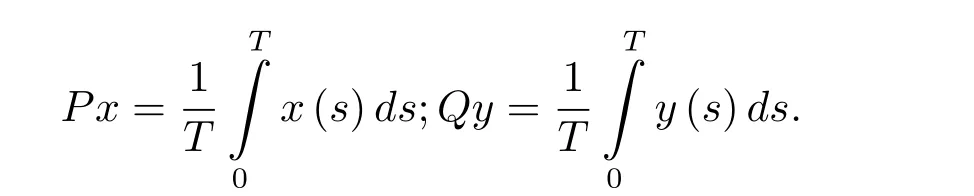
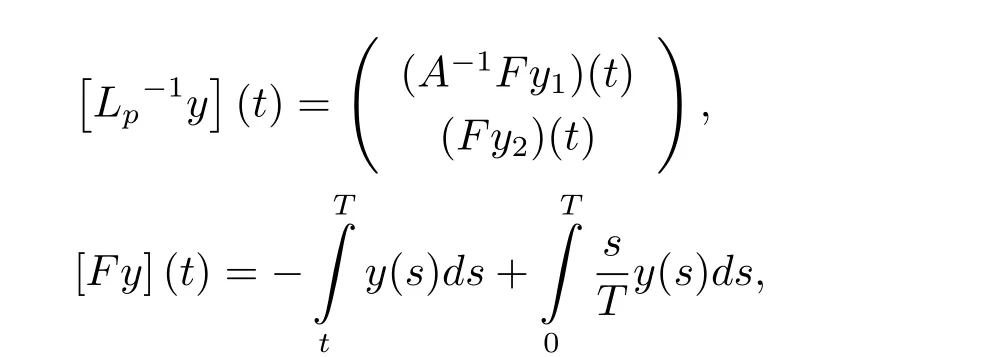
3.1 假設條件
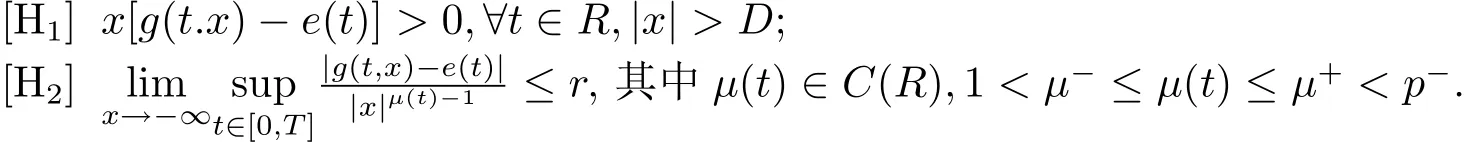
3.2 主要結論及證明