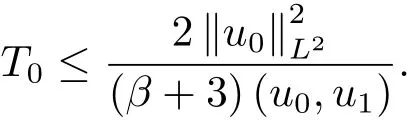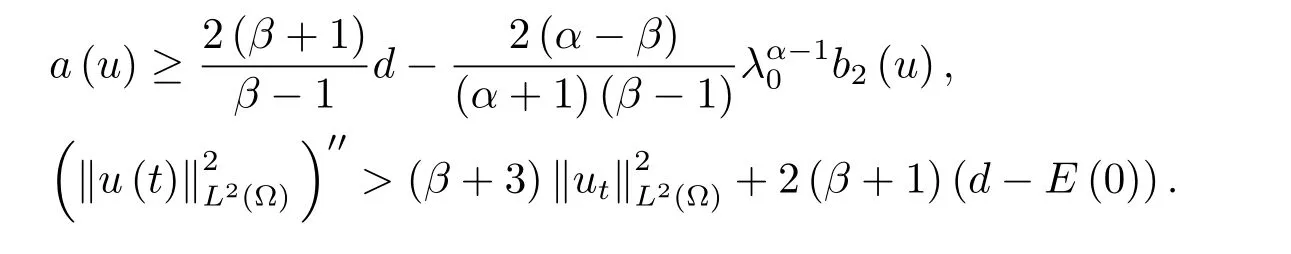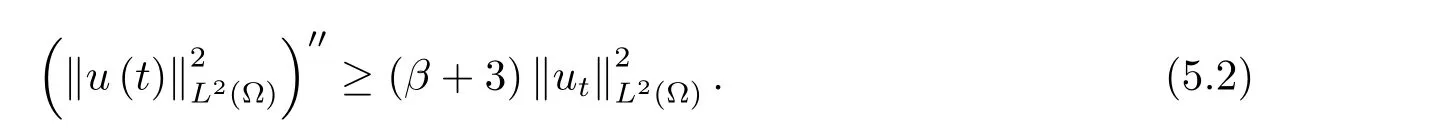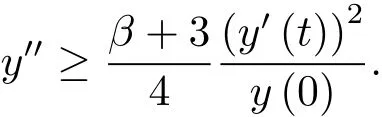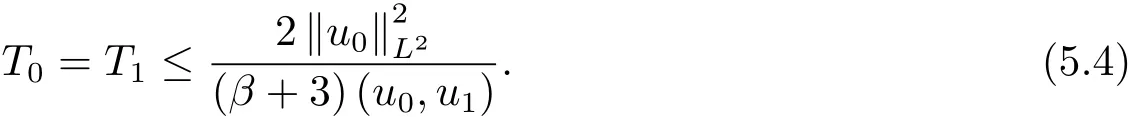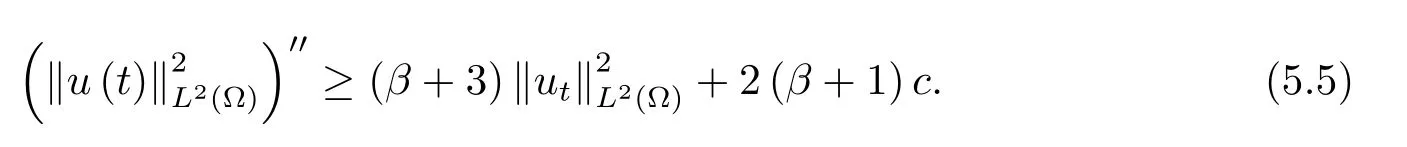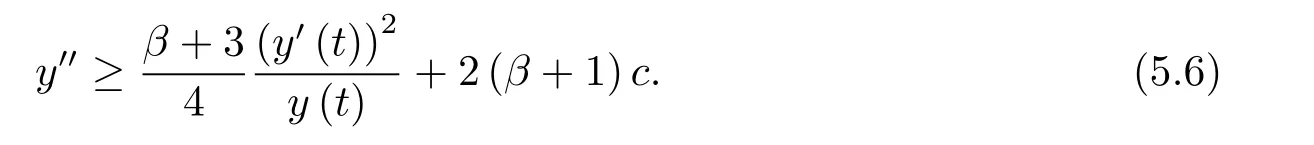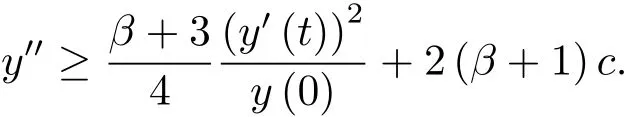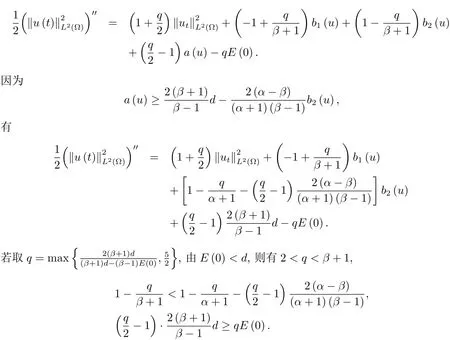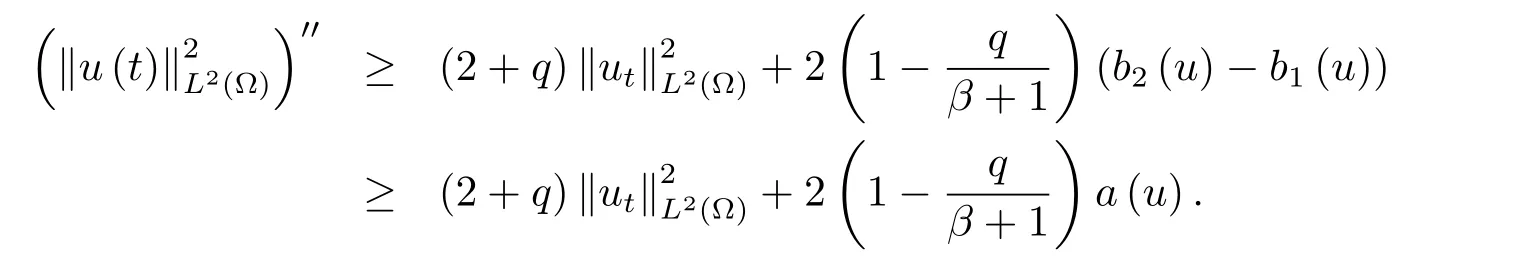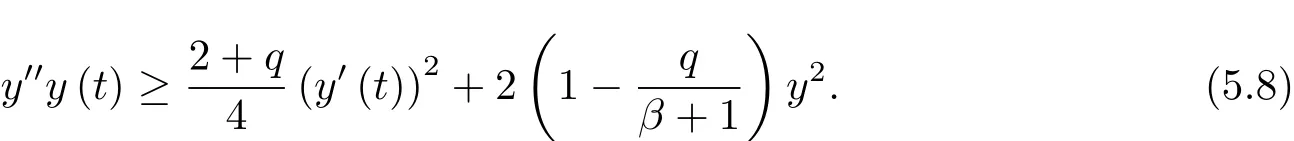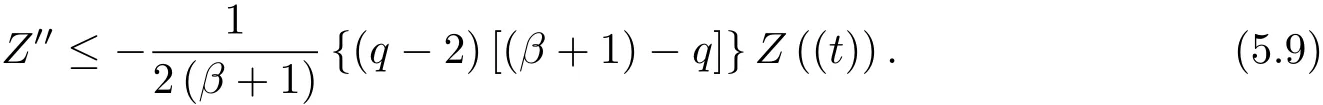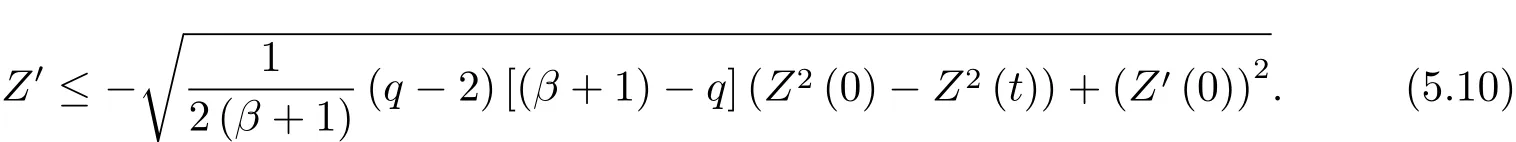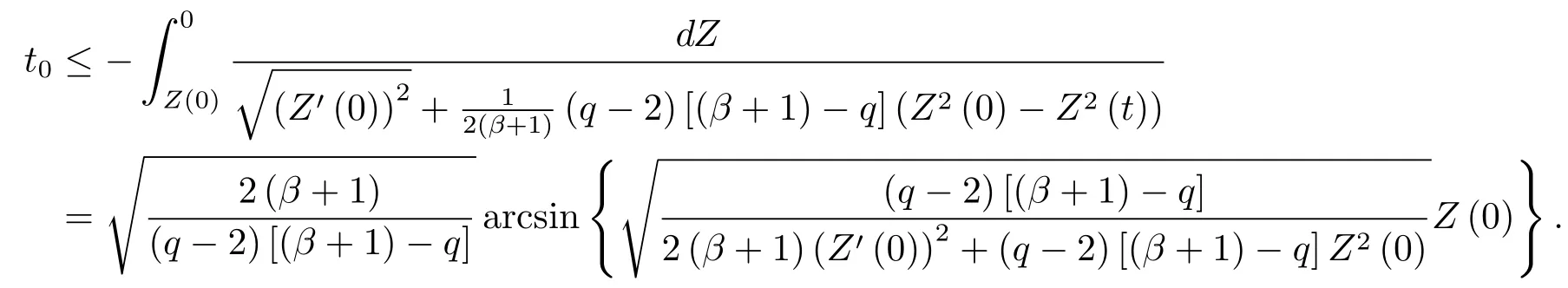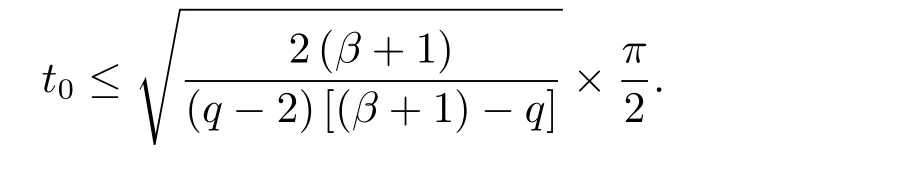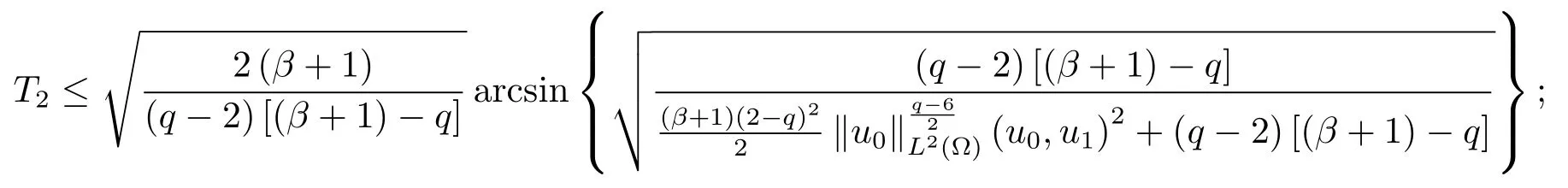一類非線性Klein-Gordon方程解的整體存在和爆破的條件
祝佳玲,李 楊,楊 晗
(西南交通大學數學學院,四川成都 611756)
1 引言
本文研究了以下非線性Klein-Gordon方程的初邊值問題
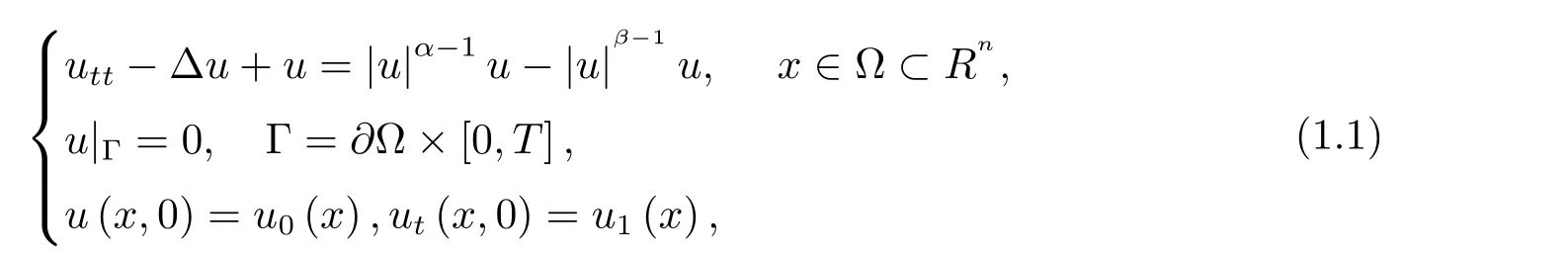
其中u=u(t,x)是復值函數,?是?上的Laplace算子,?是Rn中帶有光滑邊界Γ的有界域,1≤β<α,α=β+2,且α,β是常數.當n>2時,1;當n≤ 2時,1<α<∞.
Klein-Gordon方程是相對論量子力學和量子場論中用于描述自旋為零的粒子的基本方程.對于該類方程的研究已有一些文獻[1–9].值得特別指出的是:Shatah[1]證明了對非線性項f(u)(其中x∈Rn,n≥3,基態的存在性和不穩定性,得到了在不穩定基態下解不爆破的結果.黃文毅[2]對一類帶有阻尼項和非負勢能的非線性Klein-Gordon方程
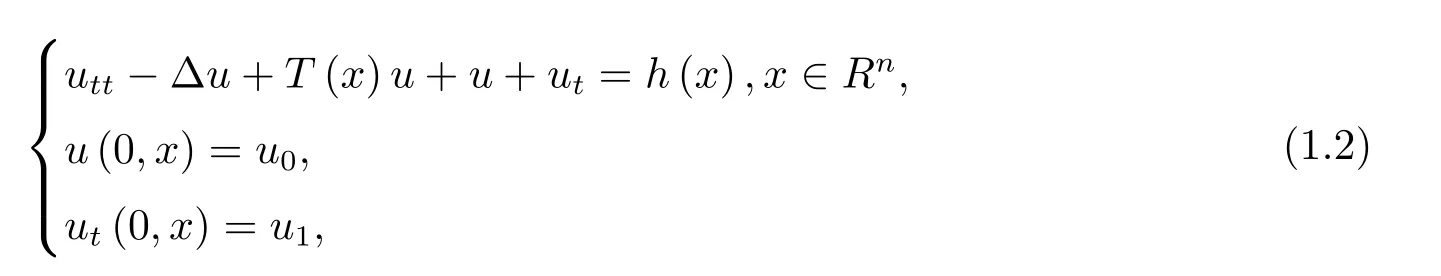
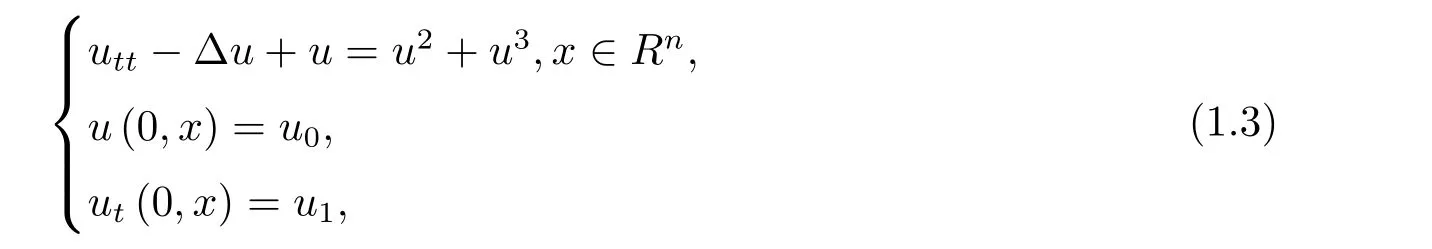
給出了當空間維數限制為n≤3時解整體存在的充分必要條件,解爆破時的生命跨度的估計等等.李考慮了不同于文獻[1]的變分問題,對上不定號的情形加以了研究,Shatah的方法對此情形不適用,這也是該文的創新之處.
本文也有類似的困難,但李[9]中方程的非線性項確定了,勢井深度的正性容易通過顯性的方程求解來確定,而本文由于非線性項中的指數不是確定的,在確定勢井深度的正性時,需要精細巧妙的討論和估計才能確定,且文獻[9]沒有考慮初始能量等于勢井深度臨界情形下的生命跨度,這也是本文的意義所在.
2 勢井深度
對u∈H1(?),n≤6,定義如下能量泛函
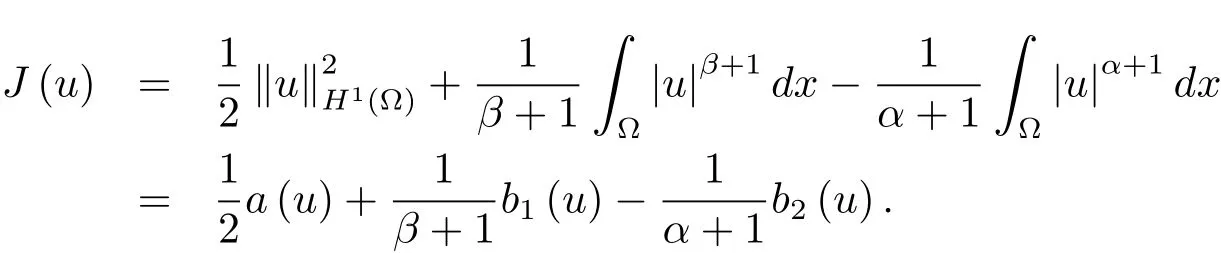
定義勢井
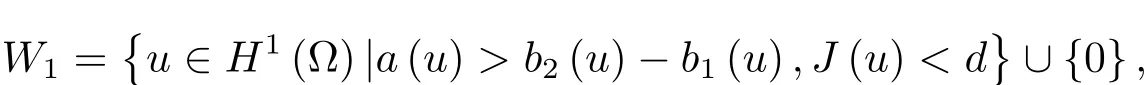
及其對應的勢井外集

為勢井深度.
下面將證明d始終大于0,即有如下引理.
引理2.1 若d由(2.1)式給出,則d>0.
證 當λ≥0時,
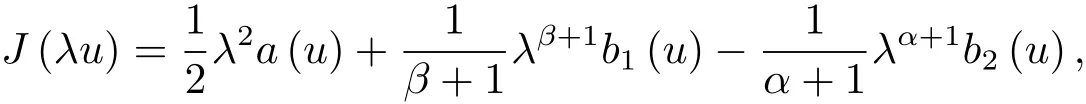
注意到 J0(λu)= λa(u)+λβb1(u)? λαb2(u)=0 存在零根.
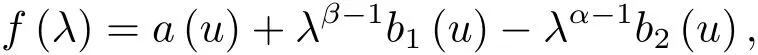
下面將證明J0(λu)=0存在正根,令注意到f(0)=a(u)>0,當λ→+∞ 時,f(λ)→?∞,因此由介值定理必然存在正根λ0,使得 f(λ0)=0,即
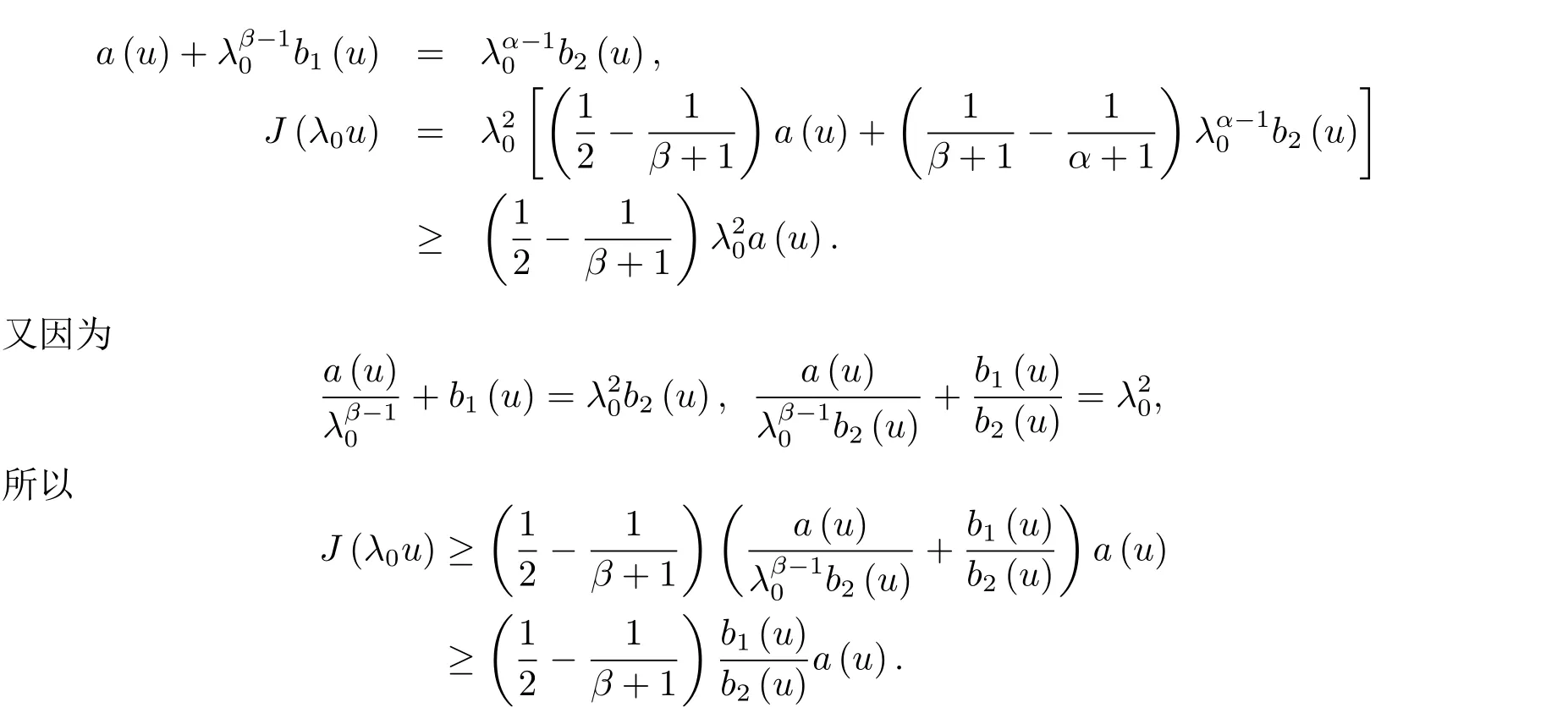
因為μ(?)<∞ (μ為?的Lebesgue測度),由β<α有
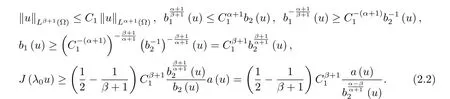
由于 H1(?) 嵌入到 Lα+1(?),有 kukLα+1(?)≤ C2kukH1(?),結合 (2.2) 式有
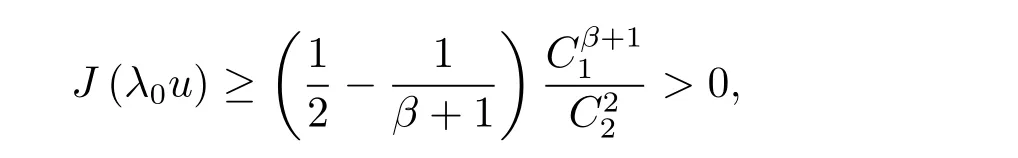
即d>0,其中c1,c2為常數.
3 解的不變集
為了得到解整體存在和爆破的條件,這一節將介紹不變集W1,W2.接下來,將利用如下事實a(u)>b2(u)?b1(u)有效等價于λ0(u)>1,a(u) 記W={u|u∈H1(?),J(u) 引理3.1W=W1∪W2,W1∩W2=?. 證 W1∩W2=?是顯然的.接下來將證明W=W1∪W2.實際上,只需證明W ?W1∪W2.容易看到等價于 a(u)=b2(u)?b1(u)>0.因此,若λ0(u)=1,則有于是,若u∈W,u 6=0,則λ0(u)6=1等價于a(u)6=b2(u)?b1(u).這意味著u∈W1{0}或u∈W2,即W?W1∪W2. (不變集)若u0,u1∈Σ(其中Σ?H1(?)為集合),則(1.1)式的解u(t,x)∈Σ,把Σ叫做問題(1.1)的解的不變集. 引理3.2若 則W1和W2是問題(1.1)解的不變集. 證 由方程(1.1)有 這意味著u∈W.通常把u(x,0,u0,u1)簡記為u(t). (1)令u0∈W1,可以斷言u(t)∈W1.若不成立,則存在t0>0,使得u(t0)/∈W1.一方面,有u(t0)∈W2;另一方面,因為a(u(t)),b1(u(t))和b2(u(t))關于t連續,由W1和W2的定義,知存在時間t?(0 若a(u(t?))6=0,則λ0(u(t?))=1.因此J(u(t?))≥d,即u(t?)/∈W,這與(3.2)式矛盾. 若a(u(t?))=0,假設0 這個矛盾說明u(t)∈W1. (2)令u0∈W2,可以斷言u(t)∈W2.假設不成立,即存在t0,使得u(t0)∈W1,則存在t?,使得 a(u(t?))=b2(u(t?))? b1(u(t?))(0 首先考慮a(u(t?))=0的情況.一方面,因為a(u(t)),b1(u(t))和b2(u(t))關于t連續,可以斷言 另一方面,因為對0≤ t 若a(u(t?))6=0,則與 (1)相同的討論有J(u(t?))≥ d,這與(3.2)式矛盾.所以u(t)∈W2. 首先研究當初始能量E(0)=d時解整體存在和爆破的條件. 定理4.1 假設E(0)=d,u0∈H1(?),u1∈L2(?). 1)若a(u0)=b2(u0)?b1(u0),且a(u0)6=0,則問題(1.1)存在整體弱解u(t,x)∈C([0,∞);(?)),ut(t,x)∈ C([0,∞);L2(?)). 2)若a(u0)>b2(u0)?b1(u0)或a(u0)=0,則問題(1.1)存在整體弱解u(t,x)∈C([0,∞);(?)),ut(t,x)∈ C([0,∞);L2(?)). 3)若(u0,u1)≥0,a(u0) 注 當(u0,u1)<0時,添上(ˉu為(1.1)式的平衡態)這個條件,同理可證,證明過程略. 證 1)若a(u0)=b2(u0)?b1(u0)且a(u0)6=0.令{wj(x)}是H1(?)的一個基,構造問題(1.1)的近似解um(t,x),使得 對于充分大的m,有 即 u(t,x)∈ C([0,∞);H10(?)),ut(t,x)∈ C([0,∞);L2(?)). 2)若a(u0)>b2(u0)?b1(u0)或a(u0)=0,可以斷言 或 a(u)=0,對所有的t≥0成立. 實際上,如果存在t1,使得 那么由于a(u(t)),b1(u(t))和b2(u(t))關于t連續,則存在t0,使得 對t0 由于a(u(t0))6=0且a(u0)6=b2(u0)?b1(u0),所以有u(t)6≡u(t0),對0≤t≤t0成立.令 v(t)=u(t0?t)6≡ u(t0),則 v(0)=u(t0),v(t0)=u0,vt(0)=ut(t?t0)=0,v(t)滿足 然而u(t0)也是以上問題的一個解,這和解的唯一性矛盾.因此(4.6)式是有效的,類似1)的證明得 u(t,x)∈ C([0,∞);H10(?)),ut(t,x)∈ C([0,∞);L2(?)). 3)與2)的證明類似,若a(u0) 若(u0,u1)≥0,則存在使得t0>0,使得(u(t0),ut(t0))實際上,若由(4.8)和(4.9)式有 對所有t≥0成立,即 是有限的.因此 由a(u),b1(u),b2(u)≥0知對所有的t≥0,a(u),b1(u),b2(u)有限.由引理3.2的證明知存在序列又由 (4.8)式知 上式矛盾.這個矛盾說明存在t1>0,使得對所有的t>0成立,因此有當然,存在t2>t1,使得因此有 對t≥t2.結果 對t>t2.因為對t>t1,對是遞減的凹函數,因此存在T<+∞,使得即 其次考慮當初始能量E(0) 定理4.2 假設n≤6,0 1)若a(u0)?b2(u0)+b1(u0)>0(或a(u0)?b2(u0)+b1(u0)=0),則問題(1.1)有整體弱解 u(t,x)∈ C([0,∞);H10(?)),ut(t,x)∈ C([0,∞);L2(?)). 2)若a(u0)?b2(u0)+b1(u0)<0,則問題(1.1)的解在有限時間內爆破. 證 1)同定理4.1中1)的證明,由E(0) 所以J(u0) 且um(0)∈W1.同引理3.2,由(4.12)式對于充分大的m和0≤t<∞,可以證明um(t)∈W1且 因此 其中 c?為常數,所以 u(t,x)∈ C([0,∞);H01(?)),ut(t,x)∈ C([0,∞);L2(?)). 2)當a(u0)?b2(u0)+b1(u0)<0時,類似定理4.1中3)的證明,易證在有限時間內爆破. 本文最后一部分將給出定理4.1和定理4.2中爆破解的生命跨度的上界估計. 定理5.1 若E(0)=d,(u0,u1)≥0,a(u0) 證 由定理4.2,對所有t≥0, 又由引理2.1的證明有 由E(0)=d,得 因為a(u0) 解上式并在0到T1上積分得 定理5.2若E(0) 1)若(u0,u1)>0,則 證 由定理4.2,對所有t≥0,同定理5.1的證明,由E(0) 因為a(u0) 將上式在0到T3上積分得 現在考慮當(u0,u1)>0時,解的生命跨度. 注意到 與(5.1)式類似可以得 由b1(u),b2(u)≥0知 因為Z0(t)<0,把(5.8)式乘以Z0,積分得 存在t0,使得Z(t0)=0,因此上式積分得 特別地,若(u0,u1)=0,即Z0(0),則 將這個結果結合(5.7)式有 1)若(u0,u1)>0,則 2)若(u0,u1)≤0,則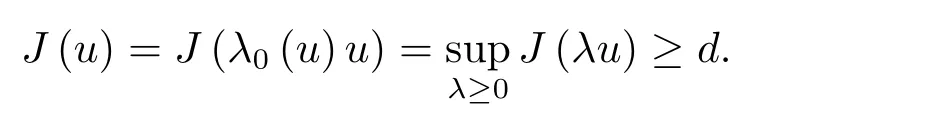
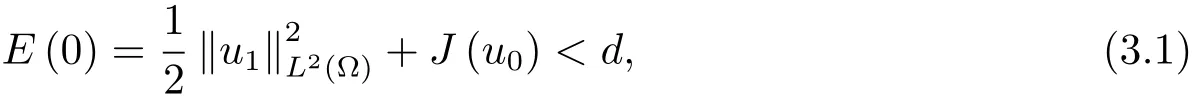
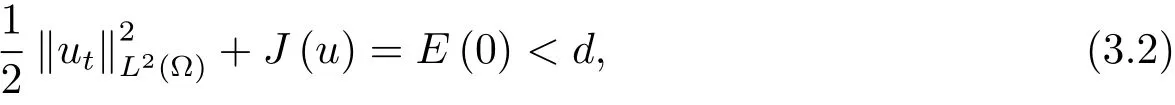
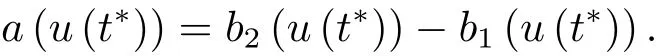
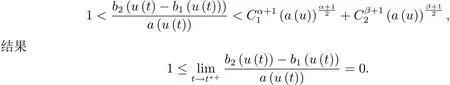
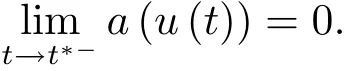
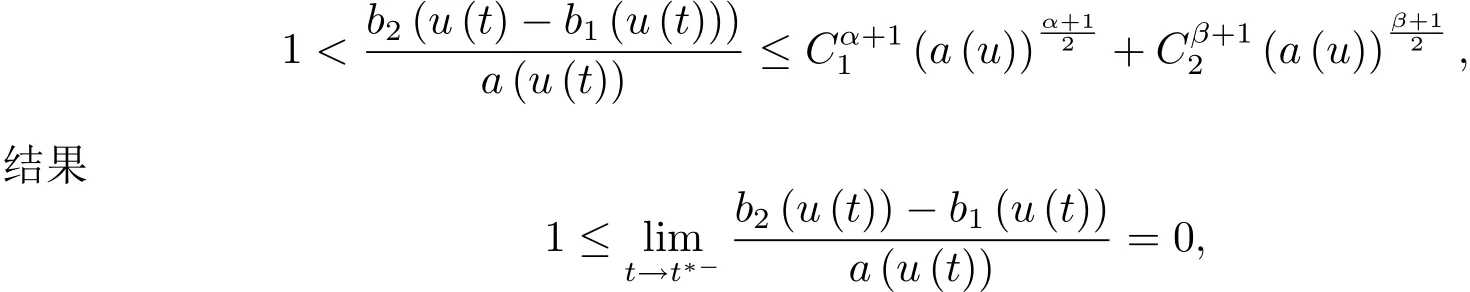
4 解的整體存在和爆破的條件
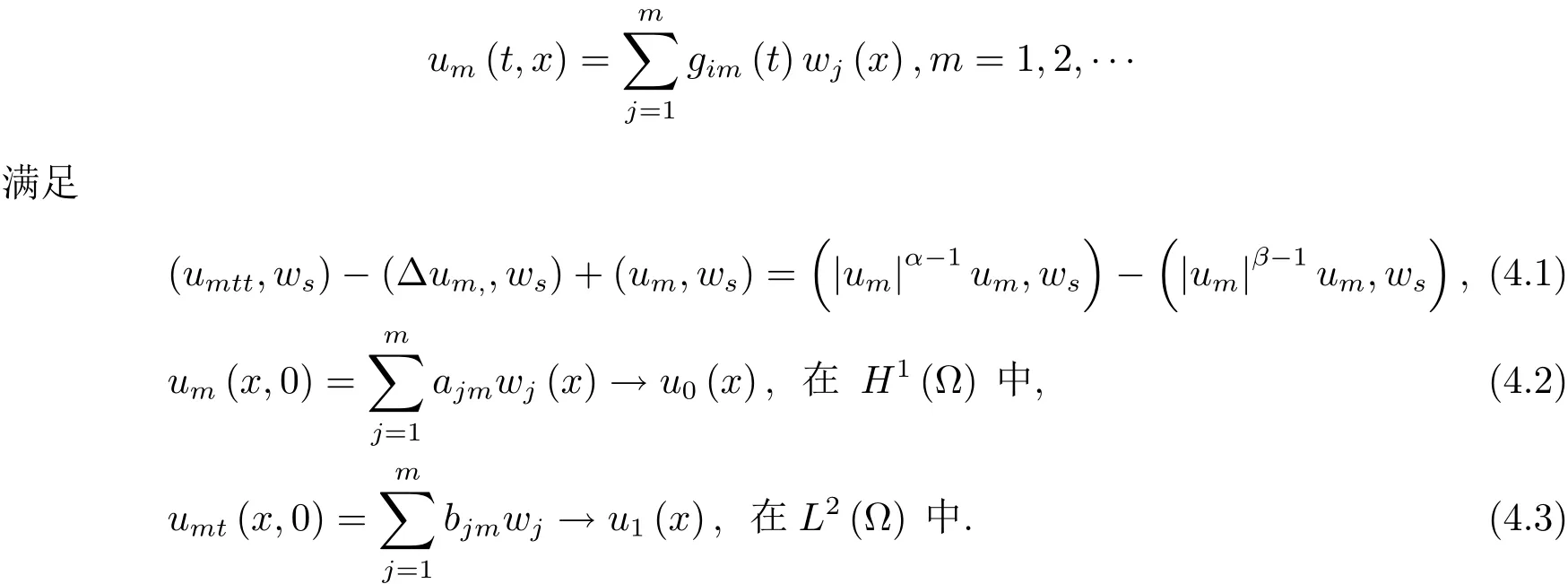
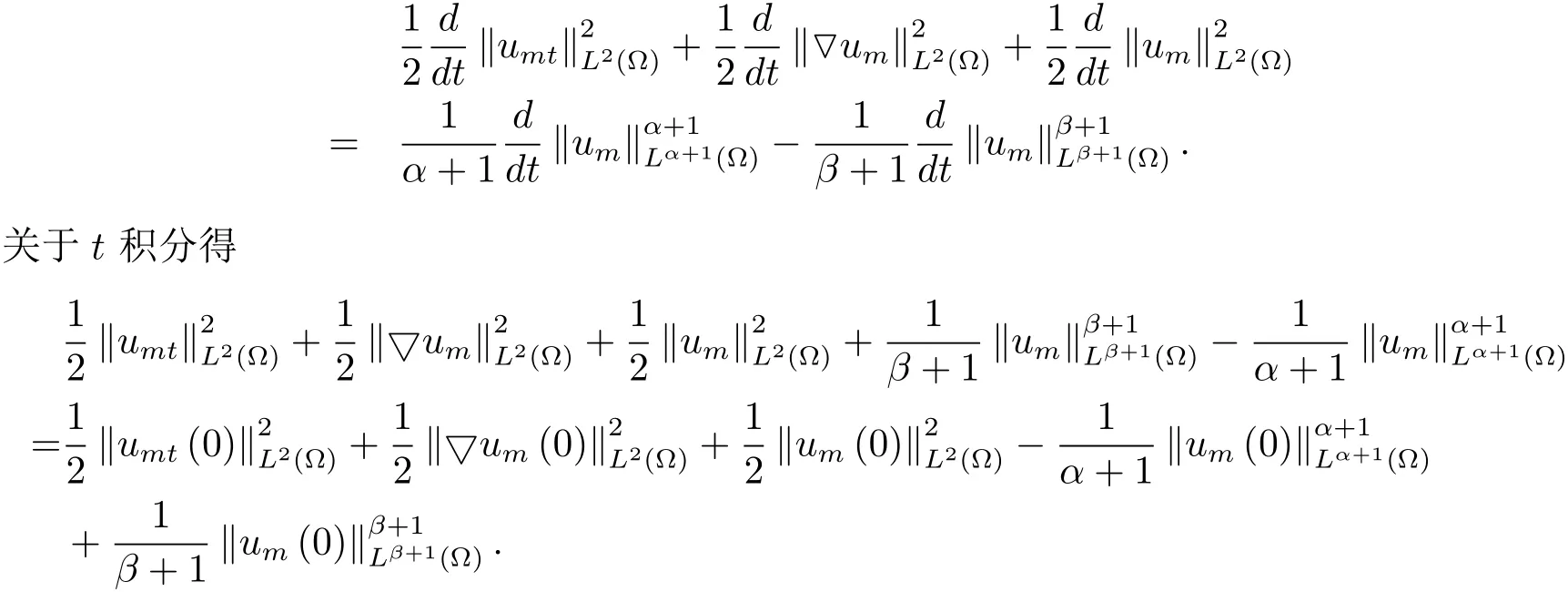
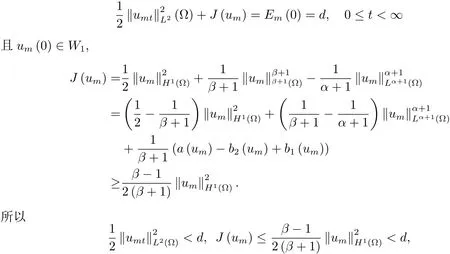
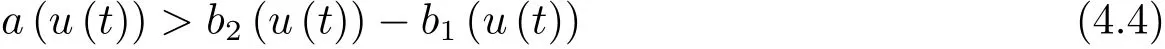

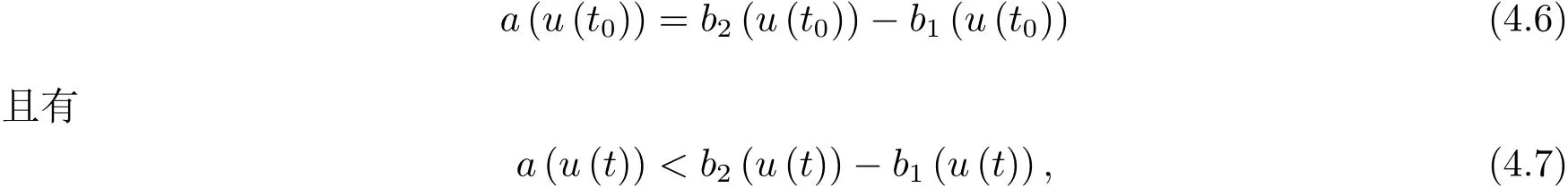
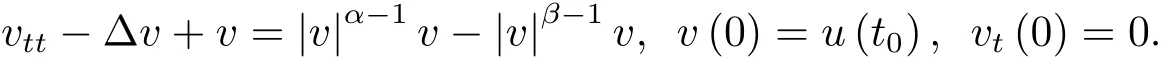


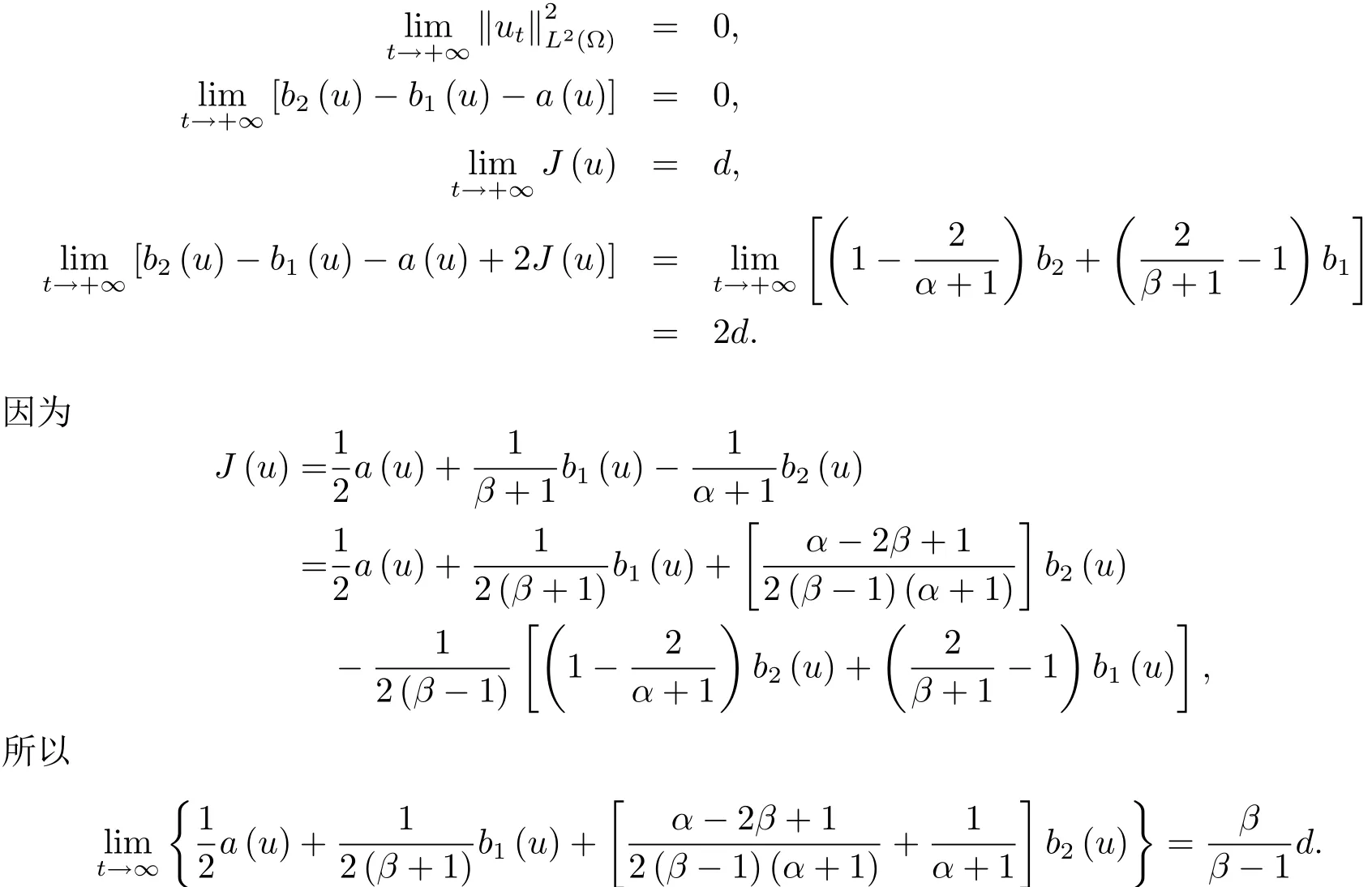
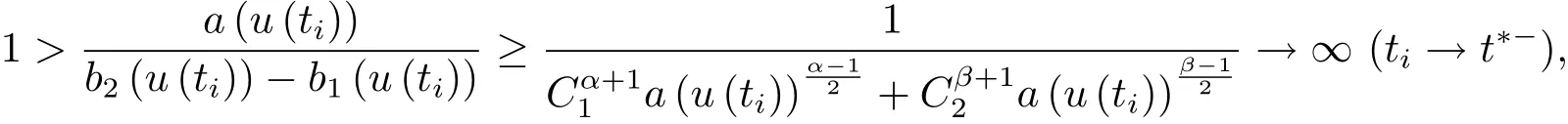

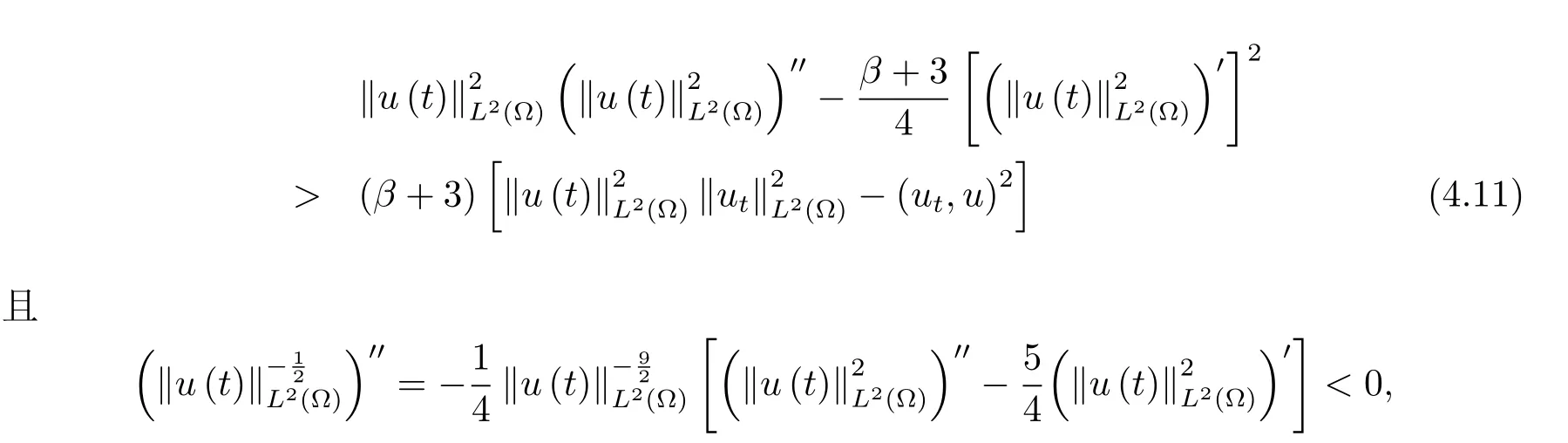
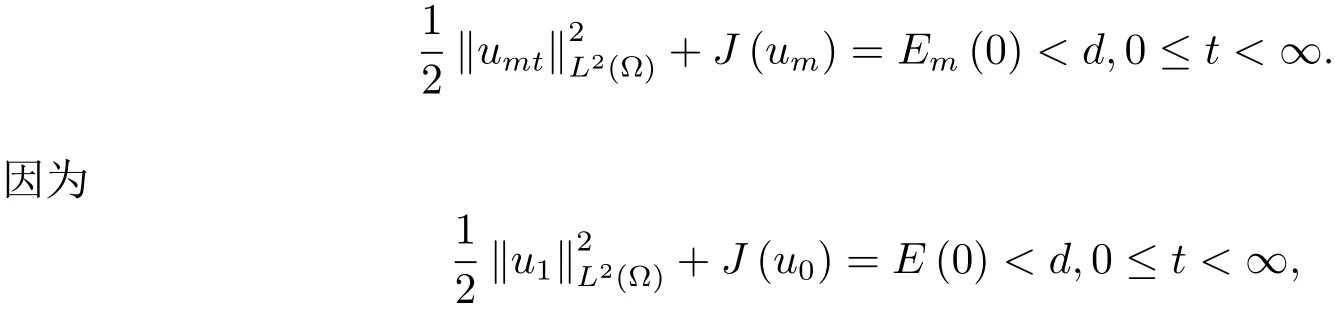
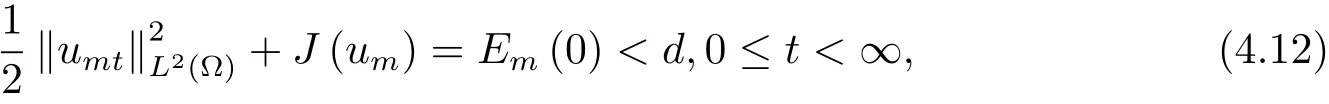
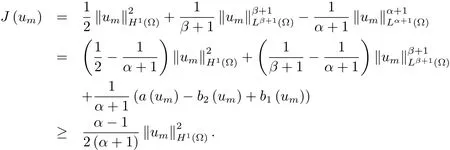
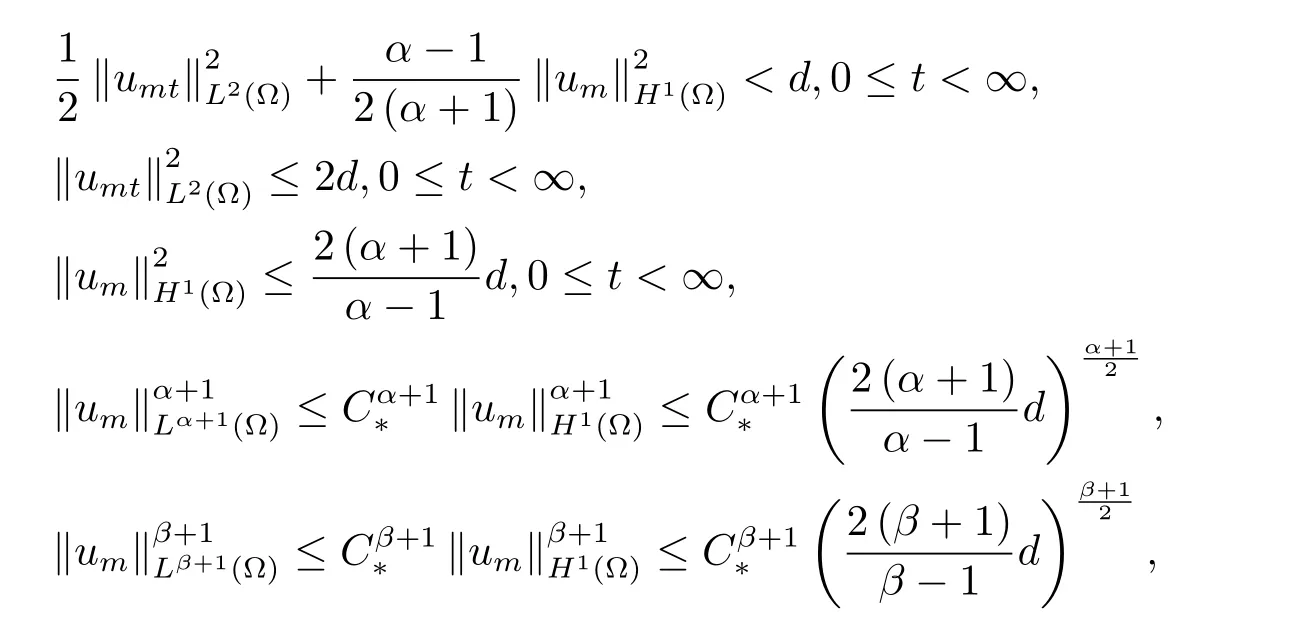
5 解爆破時生命跨度的估計