童天語，郭沛然，李潤堯

（北京師范大學，北京 100875）

1 引言

眾包（Crowdsourcing）是移動互聯技術快速發展產生的新的商業模式，最早由記著Jeff Howe[1]在美國《連線》雜志2006年6月刊上提出，目前公認的定義為“眾包指的是一個公司或機構把過去由員工執行的工作任務，以自由自愿的形式外包給非特定的（而且通常是大型的）大眾網絡的做法.（就是通過網絡做產品的開發需求調研，以用戶的真實使用感受為出發點）”[2]，也就是說眾包是一種在線、分布式問題的解決模式和生產模式.

現階段的空間眾包平臺已經日益成熟，如美團外賣、滴滴出行等眾包平臺更是與我們的生活密切相關.在目前關于空間眾包平臺的研究中，研究最多的是眾包平臺的任務分配方式，這其中大部分是關于在線決策算法的平衡的研究,也稱多臂賭博機問題[3]，而很少有關于任務定價模型的研究.實際上任務的定價在很大程度上會影響到任務完成的概率，從而影響到整個平臺的運行效率和資源配置效率.任務標價過高的話，雖然可有吸引更多會員完成任務，但并不會提高任務的完成質量，同時也容易吸引欺詐者；任務標價過低的話，任務不容易被完成，導致資源浪費[4].

因此，本文將通過對拍拍賺平臺某次任務的詳細數據進行分析，提出可行的任務定價模型，以及這類問題的一種研究思路.

2 樣本數據的描述與處理

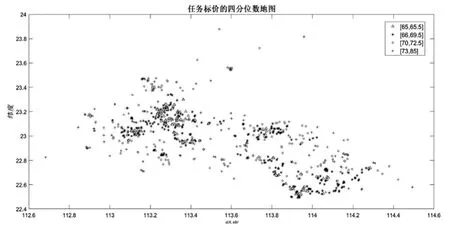
圖1

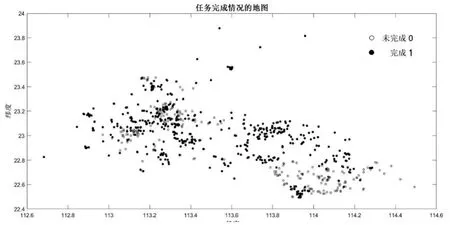
圖2

此次任務的樣本初始數據有任務的經緯度，會員的經緯度、預訂任務限額、預訂任務開始時間和信譽值.由于目標任務定價模型是以任務的相關屬性為自變量，我們需要通過這些數據生成關于任務的一些二級屬性，比如任務密度、任務周圍會員的平均信譽等，然后將這些數據的分布與下文的任務定價、任務是否完成的分布圖進行比較，選出其中對任務定價、任務完成有影響的指標，參與后續的回歸分析.

以經度為X軸，緯度為Y軸，首先運用MATLAB軟件繪制了任務定價以及任務是否完成的分布圖，見圖1和圖2.

繼而對樣本數據做相應處理，在處理中，本文最終僅選取了任務位置在經度112.68°~114.50°，緯度22.49°~23.88°之間，會員位置在經度 112.62°~115.38°，緯度 22.26°~23.64°之間的數據，因為這個范圍之外的位置數據偏離過大，會對回歸結果產生影響.同時剔除了一組異常數據：會員編號B1175.最終得到可能影響任務定價和任務完成與否的指標，此處列出10個樣本數據作為范示.

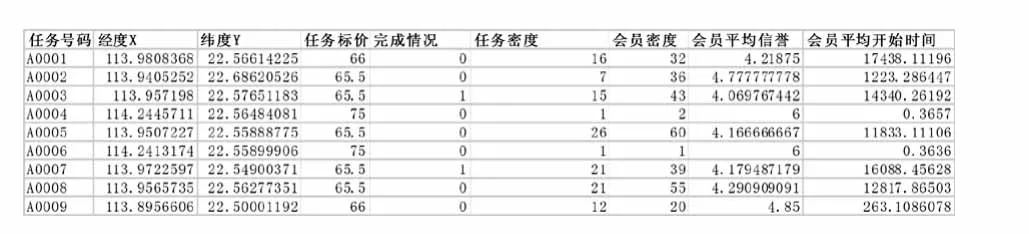
圖3

然后將數據用MATLAB軟件處理后得到的各種指標的分布圖與圖一和圖二進行比對，再加上理論上的分析，確定了下面四個對任務定價規律和任務完成情況有影響的指標：

（1）任務密度（個/25km2）：首先將經緯度換算成地表實際距離，每一緯度代表的距離為111.3214 km，每一經度代表的距離與當地的緯度有關，其中北緯22°上一經度表示實際距離102.4841km.將經緯度換算到實際距離之后，生成以該任務所在地為圓心，5km為半徑的區域內的任務數量，由此得到任一任務點的任務密度.

（2）會員密度（個/25km2）：處理方法與任務密度相同，得到每一個會員周圍5km為半徑區域內的會員數量分布.

（3）周圍會員平均信譽：將每一個任務點周圍5km半徑區域內所有會員的信譽值進行加權平均，得到該任務點的周圍會員平均信譽.由于樣本對數據的解釋中提到“任務分配時實際上是根據預定限額所占比例進行配發”，因此各會員的預定任務限額與周圍會員總預定任務限額之比即作為該會員的信譽權重，最終加總求得每一任務周圍會員的平均信譽.

（4）周圍會員平均開始時間：首先將每個會員的預訂任務開始時間處理為虛擬變量，6：30-8：00之間的一個半小時時段平均分成六份，分別賦值為1-6.然后將每一個任務點周圍5km半徑區域內所有會員的開始預訂時間進行算術平均，得到周圍會員平均開始時間.

3 任務定價的一般模型

3.1 任務定價空間計量模型的選取

3.1.1 空間相關

首先，本文引入空間相關（也稱空間交互、空間依賴）的概念：某一特定區位的經濟地理條件或特征會受到其相鄰區位的經濟地理條件或特征的影響[5].在本題目中，引入這一概念即意味著位于某一特定區域任務的定價會受到其鄰近區域的任務價格的影響.因此，除了考慮上文提出的指標對某一任務定價的影響之外，我們也應該考慮加入一個空間交互項，來描述鄰近區域任務定價的空間溢出效應.如果在回歸模型中忽略了這一重要的交互因素，即認為空間事物是同質的、無關聯的，則會導致解釋變量的系數被高估，而且誤差項不滿足同方差和漸進服從正態分布的假定，無法對系數估計進行統計推斷.

對任務定價的影響因素進行空間計量分析，第一，需要設置空間權重矩陣W.第二，需要檢驗研究對象的空間相關性，判斷相鄰區域的研究對象之間是否相互影響.第三，需要在不同的空間計量模型設定之間進行選擇.第四，分析回歸結果.

3.1.2 空間權重矩陣W的設置

首先，運用Geoda軟件，我們得出關于任務空間分布的馮洛諾伊圖（Voronoi Diagram）.圖中，每一個小圓代表一個任務的位置，實線代表邊界，邊界圍成的圖形稱為泰森多邊形（Thiesson Polygons）.該圖的性質有：（1）每個泰森多邊形中只包含一個任務點.（2）多邊形內部的任意一點到相應任務點的距離最近.在下文中，我們將一個泰森多邊形區域簡稱為一個區域[3].

圖4

其次，我們定義一個一階n×n空間權重矩陣W1，若區域i和區域j存在公共邊界或公共頂點，就定義兩者“鄰接”，Wij=1；否則，就定義兩者“不鄰接”，Wij=0；另外，Wii=0.容易看出，W 是一個對角線元素都為0的對稱矩陣.

再次，我們討論p階空間權重矩陣，Wp=(W1)p,p∈N+.以二階空間權重矩陣為例，此矩陣表示鄰居的鄰居（2階鄰居）的關系.p值越大，鄰居的數目越多，“鄰接”區域的范圍越大，不同距離鄰居的權重也不同.對于不同階數W的選擇，我們試驗性地對SEM模型進行極大似然估計，通過比較不同方程的對數似然函數值（擬合優度），選擇具有最大對數似然函數值的模型對應的空間權重矩陣[4].估計結果如下：

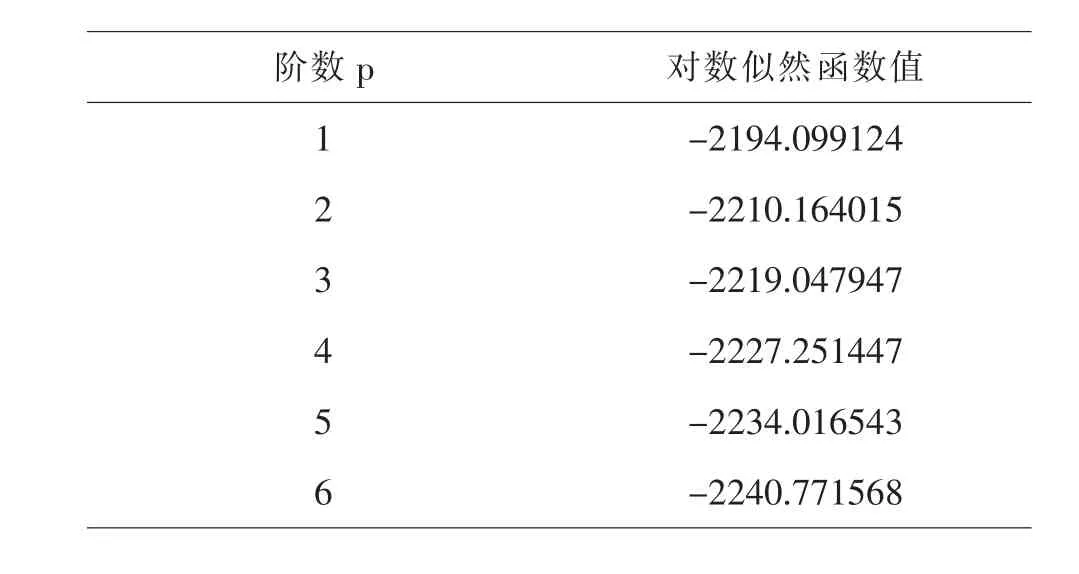
階數p 對數似然函數值1-2194.099124 2-2210.164015 3-2219.047947 4-2227.251447 5-2234.016543 6-2240.771568

從表中可知，我們應選取一階空間權重矩陣進行系數估計.

3.1.3 空間相關性檢驗

Moran(1950)提出的全局Moran I指數是檢驗區域變量空間相關性的常用方法，其定義為：

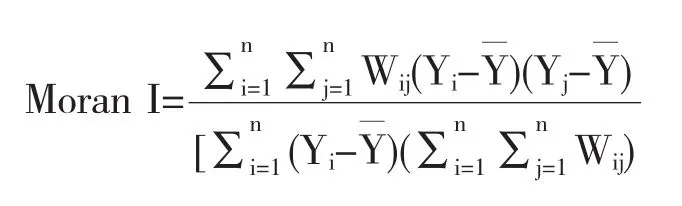
其中，Wij是空間權重矩陣第i行第j列的元素，Yi表示第i個區域的觀測值，n為區域的總數，是所有區域觀測值的平均數.Moran I指數的取值范圍是[-1,1]，且取值越靠近-1或1，空間相關性越強.當-1≤Moran I＜0時，不同區域觀測值呈現空間負相關，即一個區域的取值越大，其鄰近區域的取值越小；當0＜Moran I≤1時，不同區域觀測值呈現空間正相關，即一個區域的取值越大，其鄰近區域的取值越大；當Moran I=0時，不存在空間相關.計算任務定價的全局Moran I指數的結果如下.

（各區域任務定價的Moran I統計值）

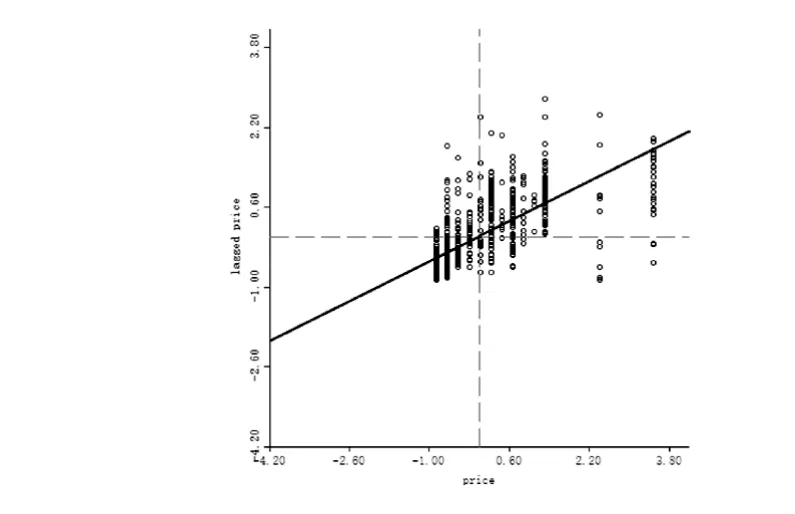
（各區域任務定價的Moran散點圖）

由計算結果可知，各區域任務定價之間存在著較強的且顯著的空間正相關性，說明任務定價的空間分布并非完全隨機的，而是表現出相似值之間的空間集聚.也就是說，從整體上看，定價較高的任務更傾向于與其他定價較高的任務相鄰近，定價較低的任務更傾向于與其他定價較低的任務相鄰近.Moran散點圖表示，大多數的觀測點位于散點圖的第一、三象限，也就是意味著，大多數的任務定價服從高-高（H-H）和低-低（L-L）的空間分布.

3.1.4 空間計量模型的選擇

空間相關性檢驗的結果顯示，對于任務定價模型的建立，如果忽視了研究對象的空間異質性和空間相關性，系數的估計和統計推斷就不準確，也不符合實際情況.因此，我們在空間滯后模型(Spatial Lag Model,SLM)和空間誤差模型 (Spatial Error Model,SEM)之間進行選擇.兩種模型的設定如下：

其中，price表示某一區域的任務定價；λ1表示空間自回歸系數，反映被解釋變量price的空間相關性，λ2表示空間誤差自相關系數，反映擾動項的空間相關性，可以理解為鄰近區域任務價格和其他空間交互因素的影響；W是空間權重矩陣；taskden表示周圍的任務密度，memden表示周圍的會員密度，goodwill表示周圍會員的平均信譽，litime表示周圍會員的平均開始時間；u、v是服從iid的隨機誤差項.

利用給定的835個任務定價數據，運用Stata軟件分別給出穩健OLS、穩健SLM和穩健SEM的估計結果.

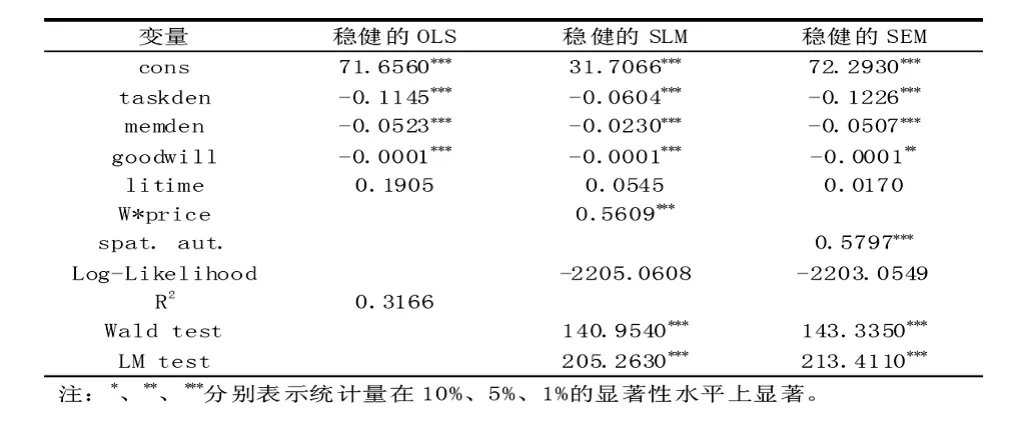
（任務定價OLS模型、SLM、SEM的穩健估計結果）

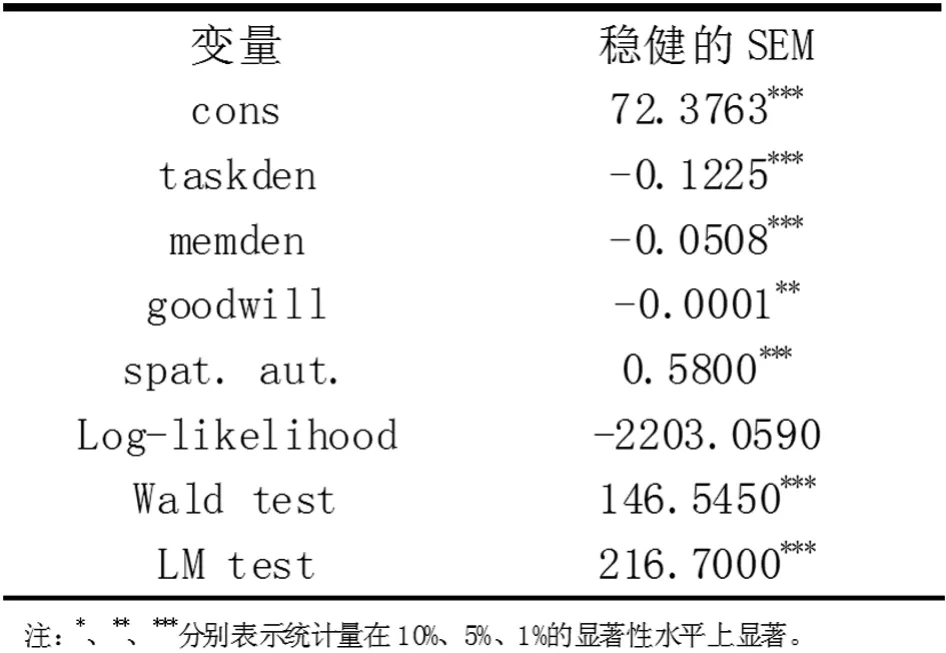
圖4

?

從回歸結果中可以看出，OLS相對于SLM和SEM高估了litime、memden兩個變量的系數，相對于SLM高估了taskden的系數，意味著若不考慮空間相關性，OLS的模型設定是欠妥的，估計的系數也是有偏的.同時，對空間自回歸系數λ1、空間誤差自相關系數λ2的瓦爾德檢驗(Wald test)和拉格朗日乘子檢驗(LM test)均在1%的顯著性水平上拒絕了系數等于0的原假設，更加證明了選取空間計量模型的科學性.通過比較SLM和SEM估計的對數似然函數值(Log-likelihood，可作為擬合優度)，我們選取對數似然函數值較高的SEM模型做進一步的估計.

3.2 空間誤差模型(SEM)的穩健估計

為了建立任務定價模型，剔除不顯著的解釋變量litime，同時為了減少隨機誤差項的異方差性，使用Stata軟件對SEM進行異方差穩健的最大似然估計[5]，結果如圖4.

由此，我們的任務定價模型可以表示為：

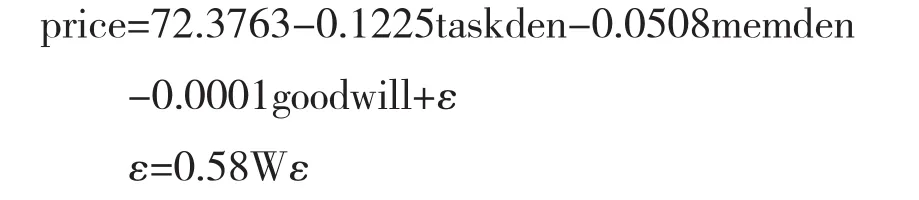
由結果可知，空間誤差自相關系數的估計值在1%的顯著性水平上顯著大于0，Wald檢驗和LM檢驗也在1%的顯著性水平上拒絕了空間誤差自相關系數等于0的原假設，表明存在誤差項空間交互效應，鄰近區域任務的價格越高，本區域任務的定價就越高.

同時我們發現，taskden、memden、goodwill這三個解釋變量的系數估計為負，說明這三個指標值越大，本區域任務價格就越低.其中，周圍5km半徑區域內的任務數量每增加1個，本區域任務的定價就會下降約0.12元；周圍5km半徑區域內的會員數量每增加1個，本區域任務的定價就會下降約0.05元.這種現象的產生可能有以下原因造成：第一，某一區域任務密度的增加意味著任務的供給增長，根據供需理論，任務的均衡價格下降.第二，某一區域會員密度的增加意味著這消費者對任務的競爭增強，更低價的任務也愿意完成，因此均衡價格下降.第三，周圍會員加權平均信譽的增加令任務發布者承擔的風險減少，任務定價的風險溢價下降.

4 模型的檢驗

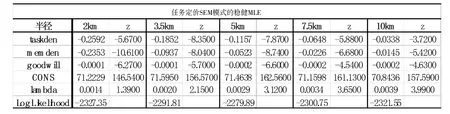
圖5

在任務定價的一般模型中，設定任務周邊空間圓形區域的參數半徑為5km.下面我們進行這一參數的變化對任務定價一般模型所得結論影響的靈敏度分析，分別用2km、3.5km、7km、10km為半徑的圓形區域來衡量.相應地，變量taskden、memden、goodwill也將因為參數半徑的改變而發生變化.在進行靈敏度分析時，我們仍然使用橫截面SEM模型進行穩健的MLE估計，下表為靈敏度分析的結果.

由圖中數據可得到如下結論：

（1）半徑的選擇對空間誤差模型中的估計系數的符號并沒有影響，taskden、memden、goodwill的系數皆為負且顯著，常數項估計皆為正且顯著，空間誤差交互系數λ的估計都為正且大都在5%的顯著性水平上顯著，說明誤差項的空間交互效應普遍存在.

（2）半徑越大，taskden系數、memden系數、常數項的估計值越小，說明隨著半徑增大，周圍任務密度、周圍會員密度對任務定價的反向作用越小；而goodwill系數、Lambda的估計值越大，說明隨著半徑增大，周圍會員平均信譽對定價的反向作用越大.而且，隨著半徑增大，定價的空間交互效應越大，即周圍任務的定價對本區域任務定價的正向作用越大.但是，由于正負系數的效應相互抵消，對最終價格的預測影響不大.

（3）從各個方程的對數似然函數值可以看出，當半徑定為5km時，Log L值為-2279.89，在5個不同半徑對應的結果數值中最大，即表明對應方程估計的擬合優度最高.因此，模型假設中選用區域參數半徑為5km是合理且可靠的.

5 結論

本文以“拍拍賺”平臺某次已結束任務的數據為樣本，研究得到該平臺上任務定價的空間計量模型.任務定價是空間眾包平臺研究中的一大難題，是影響任務完成情況的最主要因素.研究中，本文的創新之處在于考慮了空間交互的影響，設置空間權重矩陣，穩健估計出任務定價的空間誤差模型（SEM），并通過對樣本參數的檢驗，證明了提出的任務定價模型是合理可靠的.