聚焦人造地球衛星

黃愛鳳

由于人造衛星、宇宙飛船、航天飛機的問世，使人們不斷地探索宇宙，為開發宇宙新能源而努力，是當今世界先進的科學領域，近幾年針對人造衛星問題考查的頻率較高，衛星問題與現代科技結合密切，應用型試題、結合實際，正是今后高考的命題趨勢.現就衛星問題盤點如下，供同學們學習參考.

一、衛星的原理

當地球與物體之間的萬有引力恰好提供物體圍繞地球做勻速網周運動的向心力時，物體就會圍繞地球永遠運動下去，就成了地球的人造衛星.

二、衛星軌道

衛星運動時，地球對其萬有引力提供向心力，所以衛星的軌道平面必過地球球心.其可能軌道分別如圖1、2、3所示.但衛星不可能位于某一緯度平面上，如圖4所示，原因是衛星僅受一個萬有引力作用，這個萬有引力將分解成垂直地軸的向心力和指向赤道面的分力，由牛頓第二定律可知，衛星將會在該方向上加速而脫離緯度平面.由于地球的白轉，圖2所示衛星軌道平面不可能總和某一經線圈所在平面重合.

三、人造衛星的線速度、角速度、周期與軌道半徑的關系

從以上各式可以看出：人造地球衛星的周期、線速度、角速度與它所在的軌道相對應，與衛星本身的質量無關，即同一軌道上的衛星具有相同的周期、線速度、角速度及加速度.

四、同步地球衛星（通信衛星）

1.所謂的同步地球衛星就是相對地球靜止的和地球具有相同周期的衛星，T=24 h.

2.同步地球衛星必位于赤道的上方，相對地面的高度為定值，與地球的自轉方向相同.

五、宇宙速度

空運行時，半徑r最小，運行速度最大，稱為第一宇宙速度，其大小為7.9 km/s.第一宇宙速度是衛星發射的最小速度，是衛星運行的最大環繞速度.這里的規律同樣適用于其他星體.

2.衛星能掙脫地球引力的速度，稱為第二宇宙速度（脫離速度），其大小為11.2 km/s.

3.衛星能掙脫太陽引力的速度，稱為第三宇宙速度（逃逸速度），其大小為16.7 km/s.

六、衛星的發射、回收和對接

1.衛星的發射速度要求大于或等于7.9 km/s，小于11.2 km/s.

衛星的高度越高，要求發射的速度就要越大，在上升過程機械能守恒，動能轉化成勢能，速度逐漸減小，到達該軌道的速度都要比低軌道的速度小，同一衛星所在處的軌道越高，機械能越大.

2.發射同步衛星一般采用變軌發射的方法

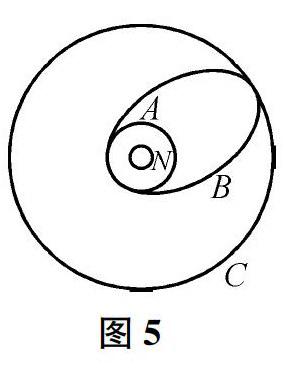
首先利用第一級火箭將衛星送到180-200 km的高空，繞地球做勻速網周運動，該軌道為停泊軌道A.當到達赤道上空時，第二、三級火箭點火，此時衛星的速度增加，萬有引力不足以提供向心力而發生離心運動，進入赤道平面內的橢網軌道B.當衛星到達最遠點時，恰好到達同步軌道c，由于克服地球引力做功速度減小，萬有引力大于所需的向心力，因而要在該處啟動衛星發動機，提高衛星的速度，使萬有引力恰好提供向心力，衛星就停留在同步軌道c上，如圖5所示.

3.衛星的對接和回收

衛星對接：由于衛星的運動僅有萬有引力控制，同軌道衛星速率相同，加速則發生離心而高于本軌道，因而要求從低軌道上加速才能實現對接.

衛星的回收：衛星在網軌道上正常運行時，萬有引力恰好提供向心力，要想回收則必需產生一個指向地心的加速度.因而只有先將衛星減速后，萬有引力提供向心力后還可以產生一個指向地心的加速度，回收過程中由于重力做功，速度不斷增大（可見減速是瞬時的，最終速度增加），角速度增加，周期減小，加速度越來越大.

七、人造地球衛星用途分類

（1）科學衛星

科學衛星是用于科學探測和研究的衛星，主要包括空間物理探測衛星、天文衛星、生物衛星和空間微重力試驗衛星等，用來研究高層大氣、地球輻射帶、地球磁層、宇宙線、太陽輻射等，并可以觀察其他星體.

美國發射的第一顆衛星“探險者”號就是一顆科學探測衛星，以后“探險者”發展成一個科學衛星系列，它們主要用于探測地球大氣層和電離層；測量地球高空磁場；測量太陽輻射、太陽風；探測行星際空間等.

我國的“實踐一號”衛星裝有紅外地平儀、太陽角計等探測儀器，取得了許多環境數據.“實踐二號”和二號甲、二號乙是用一枚火箭同時發射的三顆衛星.其中“實踐二號”外形為八面棱柱體，任務是探測空間環境，試驗太陽電池陣對日定向姿態控制和大容量數據存儲等新技術.

（2）技術試驗衛星

技術試驗衛星是進行新技術試驗或為應用衛星進行試驗的衛星.航天技術中有很多新原理、新材料、新儀器，其能否使用，必須在天上進行試；一種新衛星的性能如何，也只有把它發射到天上去實際“鍛煉”，試驗成功后才能應用；人上天之前必須先進行動物試驗……這些都是技術試驗衛星的使命.

（3）應用衛星

應用衛星是直接為人類服務的衛星，它的種類最多，數量最大，其中包括：通信衛星、氣象衛星、偵察衛星、導航衛星、測地衛星、地球資源衛星、截擊衛星等.

我國1988年9月7日發射了第一顆氣象衛星一“風云一號”太陽同步軌道氣象衛星.衛星云圖的清晰度可與美國“諾阿”衛星云圖媲美，但由于星上元器件發生故障，它只工作了39天.后成功發射了四顆極軌氣象衛星（風云號）和三顆靜止氣象衛星（風云二號），經歷了從極軌衛星到靜止衛星，從試驗衛星到業務衛星的發展過程.

八、典例分析

例1 地球赤道上有一物體隨地球一起自轉做圓周運動，所受的向心力為F1，向心加速度為a1，線速度為v1，角速度為ω1；繞地球表面附近做圓周運動的人造衛星（高度可忽略）所受的向心力為F2，向心加速度為a2，線速度為v2，角速度為ω2；地球同步衛星所受的向心力為F3，向心加速度為a3，線速度為v3，角速度為ω3；地球表面重力加速度為g，第一宇宙速度為v，假設三者質量相等，則

（）

A. F1=F2>F3

B.al=a2=>a3

C.vl=v2 =v>v3 D.ωl=ω3<ω2

例2 自1964年8月美國成功發射第一顆同步通信衛星以來，同步衛星給人們的生活帶來很大的方便.例如，打開電視，我們就可以收看到很多經同步衛星傳送的節目.衛星直播已成為日常用語.同步衛星所在的軌道稱為同步軌道.若已知地球表面的重力加速度為g.地球半徑為R，地球自轉周期為T，試回答以下問題：

（1）為了使同步軌道上的衛星互不影響，每兩顆星之間要間隔100 km，則同步軌道上最多能同時存在多少顆同步衛星？

（2）世界上有很多發射同步衛星的航天發射場均盡可能建在靠近赤道的地方，這樣有何優點？

（2）越靠近赤道的地方，物體隨地球自轉的線速度越大，初動能越大，越有利于減少發射時所消耗的能量（或同步軌道在赤道平面內，越靠近赤道，越有利于減少發射難度）.

例3 一顆在赤道上空運行的人造衛星，其軌道半徑r =2R（R為地球半徑），衛星的運動方向與地球自轉方向相同.已知地球自轉的角速度為ω，地球表面處的重力加速度為g.

（1）求人造衛星繞地球轉動的角速度.

（2）若某時刻衛星通過赤道上某建筑物的正上方，求它至少經過多長時間再次通過該建筑物的正上方.