基于核心內容的試題命制*
——以一道導數原創題的命制過程為例

●張 瑋 胡 滿 (學軍中學，浙江 杭州 310012)

0 引言

2018年3月，筆者在參與A校高三年級的一次考試命題時，需要提供一道有關導數的試題．筆者認為命制的試題應側重于考查該學科的主干知識，考查主干知識應側重于考查其中的核心內容．在高中階段，以導數的計算、求函數的單調區間作為導數內容的重中之重，而求函數的最大值、最小值、用導數證明不等式、求曲線的切線等內容，都是在求得函數的導數或單調區間之后的一些衍生產物．

2017年是浙江省高考改革后，文理不分科的第一年高考．這一年的高考導數題，主要考查了求函數的導數、求函數的單調區間和值域的問題．雖然2017年浙江省數學高考試題的總體難度明顯下降，但是對學生數學能力的考查沒有下降．就導數這一塊內容而言，2017年的試題對于導數核心內容的考查絲毫沒有減少，反而用一種更加直接的方式呈現了出來．因此，筆者認為在新高考的背景下，試題應突出用導數求單調區間這部分內容．經過反復研磨，最終給出了一道由筆者獨立編擬的導數原創題(例1)．該題主要考查導數的計算和求函數的單調區間，在此基礎之上，進而考查函數最小值的問題．

例1設f(x)=x－ln(ax+a+1)+1．

1)若a=1，求f(x)的單調區間;

2)若對于任意x≥－1，不等式f(x)≥0恒成立，求a的最大值．

綜上可知，a的最大值為1．

1 編題的背景

導數是高等數學的基礎內容，可以用它來刻畫函數的凹凸性，該性質是函數的一個很重要的性質，它可以通過二階導數的符號來確定．在高中階段，導數只是用來求函數單調區間的一個有力工具，而求函數單調區間的重要性在于求函數的最值(極值是局部的最值)．在已知最值之后，很多問題才能展開，比如證明不等式等問題．在有關導數的試題中，指數函數f(x)=ex是“常客”，而且它在(0，1)處的切線為 y=x+1，并且當 x≥0時，滿足ex≥x+1．這個不等式非常重要，不僅是因為它蘊含了曲線和切線的位置關系，而且它還可以通過適當的代換，得到很多有用的結論．如:

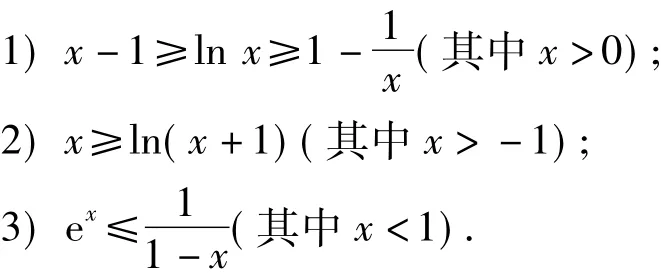
這些不等式的應用活躍在各種考試當中，比如:

例2已知數列{xn}，滿足x1=1，xn=xn+1+ln(xn+1+1)(其中 n∈N)，證明:當 n∈N*時，

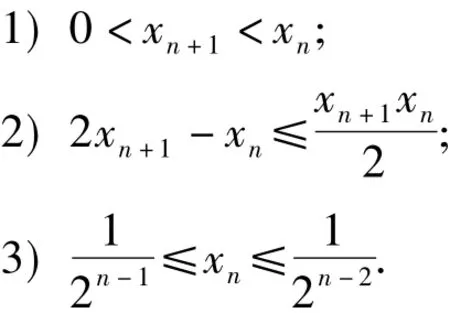
(2017年浙江省數學高考試題第22題)

1)略．

2)分析原命題等價于，即證明

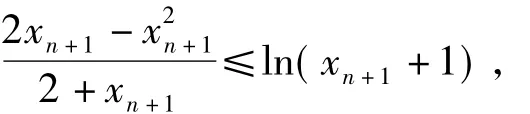
利用結論1)的右邊不等式，即得．

3)分析利用結論2)，放縮后可得

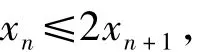
即

因此左邊的不等式得證(右邊證明略)．

從中可以看出高考試題對此類不等式也青睞有加．此外在高等數學中，函數f(x)=ex在x=0處的泰勒展開式為

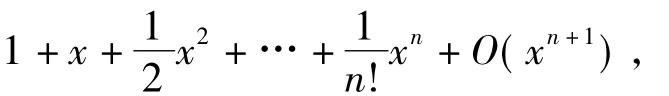
因此不等式ex≥x+1還具有一定的高等數學背景．在高中階段，由于教材對函數的二階導數要求不高以及高考導數試題的難度下降等原因，沒有選擇不等式．但是對于不等式ex≥x+1，筆者希望它能動起來，故考慮再加個參數．不等式ex≥x+a顯然過于簡單，從而考慮ex≥ax+1;再由y=x+1和f(x)=ex的位置關系可知，a≤1，于是原創題(例1)的函數模型f(x)=ex－ax－1就此確定．之后筆者在2012年湖南省數學高考理科試題中發現了它的蹤跡:

例3已知函數f(x)=eax－x(其中a≠0)．

1)對任意x∈R，f(x)≥1恒成立，求實數a的取值集合;

2)略．

(2012年湖南省數學高考理科試題第22題)

分析令t=ax，則 eax－x≥1，從而

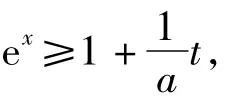
由此原不等式轉化為不等式ex≥1+ax的形式．

模型確定之后，接下來的問題就是考什么?由于導數部分的核心內容是導數的計算和函數的單調區間，因此命題方向不能偏．筆者設想:第1)小題可以求單調區間;第2)小題可以設置一些已知條件，然后求參數a的范圍或最大值．大方向基本確定了，那么在導數的計算中如何考查?大多數函數的求導中都會包含四則運算，而復合函數的求導過程中，必定包含了基本初等函數的求導公式．因此筆者的想法是:先構造一個函數，得到試題的雛形;然后再通過適當的改造使得函數結構符合考查要求．

2 編題的過程

筆者希望通過求導之后得到一個可以因式分解的式子，方便學生得到該函數的單調區間，從而降低第1)小題的難度．得到試題的第1稿為:

第1稿已知函數f(x)=ex(1+ax+x2)．

1)若a=1，求f(x)的單調區間;

由于第2)小題形式不夠美觀，筆者對此不太滿意，因此想到對不等式作變形，便有了第2稿:

第2稿已知函數f(x)=ex(1+ax+x2)．

1)若a=1，求f(x)的單調區間;

這一稿雖然形式上比第1稿漂亮了點，但是ex出現了兩次，且函數f(x)中也有因子ex，感覺過于累贅，且拼湊的痕跡也太過明顯．筆者意識到:若不改變函數的結構，上述兩稿的問題解決起來相對比較困難，那么該選用什么函數呢?因為最后都歸結到不等式ex≥ax+1，所以可以通過對x進行賦值來改變函數的結構．從第2稿不等式的形式，筆者得到了啟發，便有了第3稿:

第3稿已知函數f(x)alnx．

1)若a=1，求f(x)的單調區間;

2)若對于任意x＞0，不等式f(x)≥0恒成立，求a的最大值．

第3稿雖然解決了之前兩稿的問題，但是函數較為復雜．特別是第1)小題，學生能否求出單調區間，這成為筆者心頭的又一擔心．經過求導發現

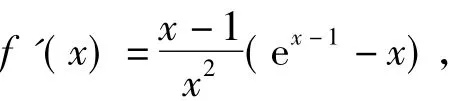
利用ex－1≥x這個結論，第1)小題不難求出．但是對于第2)小題，如果按照筆者的思路去求解，則需要利用等式將問題進行轉化，而這是個難點，學生很難想到．回顧平時的課堂教學，要解決第2)小題，學生應該還有兩種方法:

方法1進行參變量分離．原不等式化為

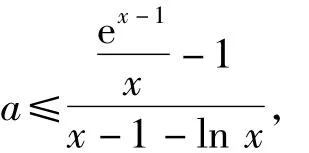
然后再求當x＞0時，不等式右邊式子的最小值．

對學生而言這顯然很困難，故此路不通．

方法2直接求原函數的最小值，只需要最小值非負即可．經過求導，得

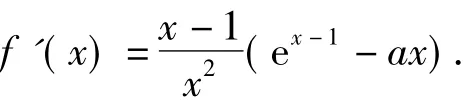
因單調區間不容易求出，故此路不通．由此看來，要解決第2)小題似乎只有“華山一條路”，即只能沿著筆者的設計思路去求解．

若此題作為“老高考”的壓軸題，也許還合適;若作為“新高考”的試題，顯然也不合時宜，入口太窄，難度太大．一個好的試題，應該有多個入口供學生選擇，可以通過不同的角度來詮釋．因此，筆者決定繼續改．考慮對第3稿的函數作代換，于是決定將x換成x+1，得到函數

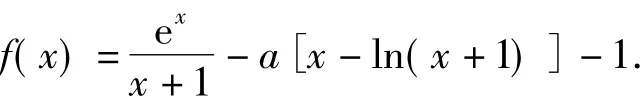
1)求f(x)的單調區間;

2)若不等式f(x)≥1+alnf(x)恒成立，求a的最大值．

第4稿的題干顯然更簡潔，只是第2)小題中，很容易聯想到換元，會使得大部分學生的解法都一樣，筆者對此不滿意，故繼續修改．由于第3稿是用不等式x－1－lnx≥0對x進行賦值，才使得函數變得復雜，因此想要讓解析式更簡單，就只能簡化賦值的式子．筆者采用了第4稿的賦值方式，再對兩邊取對數，這樣就得到了試題(即例1)．

3 試題的另解

在試題的命制過程中，筆者獲得了第2)小題的其他兩種解法．

解法2當a≤0時，顯然符合，故只需考慮a＞0的情形．令 g(x)=ex－ax－1，則

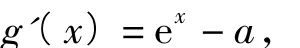
即函數g(x)在(lna，+∞)上單調遞增，在(－∞，lna)上單調遞減．

若a≤1，則 g(x)≥g(0)=0;若 a ＞1，則g(x)≥g(lna)=a－alna－1，因為 ln1＜1－1，aa所以g(lna)＜0．

因此，a的最大值為1．

解法3考慮參數分離:經檢驗a=1符合條件，即a的最大值為1．

4 考后的反饋

考后筆者參與了本次考試的閱卷，得到如下數據:本題滿分15分，平均得分10．6分;40%左右的學生，得分不小于14分;10%左右的學生第1)小題求導數錯誤;還有30%左右的學生在做第2)小題時，出現了困難，得分很低，但是都猜出了答案．從得分情況來看，本題的區分度還可以．大部分學生對于高考要求的復合函數求導、求函數的單調區間問題掌握得很好，少部分學生還需要加強導數計算的訓練．本題第2)小題，可以通過使［－1，+∞)上的最小值非負得到參數a的最大值．從得分情況來看，求函數在給定區間上的值域問題，還需要加強訓練．第2)小題的解答，部分學生使用了解法3，參數分離之后，部分學生使用了高等數學中的洛必達法則，還有部分學生繼續用導數求式子最小值．另外從學生的解答中，筆者發現了兩種新解法如下:

解法4由第1)小題可知，當a=1時，

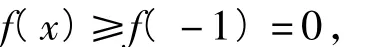
矛盾．

綜上可得:a的最大值為1．

解法5當a=0時，f(x)=x+1，顯然符合，故a的最大值非負．因為f(－1)=0，故存在δ∈( －1，0)，使得在( －1，δ)內，函數 f(x)單調遞增，即導函數f'(x)在(－1，δ)內恒非負．又

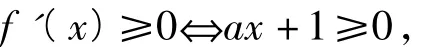
5 考后的反思

從考生答題的情況來看，大部分學生并沒有被不等式x－1≥lnx卡住，反而給出了更漂亮的解法．從學生的整體答題情況來看，本文中提到的5種解法都有學生用到，解法的多樣性是筆者在命題時所沒有料到的．本題入口寬，解法多樣，由此來看，應該是一個好的訓練題．從第2)小題的答題情況來看，錯誤百出，這反映出部分學生的基本功不夠踏實．2017年的浙江省數學高考導數試題突出導數計算和函數單調區間的考查，因此，在高三臨考階段，對于基礎薄弱的學生，應該要更加重視核心內容的訓練和講解，做到有的放矢．

再次翻看學生的解答，筆者發現有少數學生因為沒有處理好不等式，導致第 2)小題沒有拿到高分，主要原因是不熟悉x－1－lnx≥0．因此若將第1)小題改為“當a=1時，令g(x)=f(x－2)，求g(x)的單調區間和最小值”可能會更好一點．考完后，筆者又重新翻看了2017年浙江省數學高考導數試題，函數中沒有參數，不需要討論，干干凈凈地考函數．因此，筆者認為:若把例1當作是一般的訓練題，比較適合;若當作是高考模擬題，則不太適合．這也啟示筆者:在編擬試題時，應盡可能地與高考試題接軌，讓高三的師生明確方向．