基于建構主義的數學解題教學案例分析

付敏

（南昌市第十中學，江西南昌 330006）

1 教學課題

本文選取的教學課題是函數值范圍問題的求解。

2 教學目標

（1）理解函數中自變量與函數值的相互對應和制約關系。

（2）創設問題案例，通過啟發來誘導學生發現數學邏輯錯誤和矛盾，通過由特殊到一般、從具體到抽象，深刻剖析錯誤原因，培養學生數學思維能力。

（3）通過對學生學習認識策略的指導，培養學生學習反思的良好思維習慣，發展學生智力。

3 教學重點、難點

重點：掌握求函數值及其范圍的方法。

難點：理解該方法的原理及內涵。

4 教學方法

本文選取的教學方法是建構式教學法。

5 學生的現狀

已學好函數的概念，理解自變量與函數的相互關系及函數值的求法，并能運用函數的知識去解決簡單求值問題的高一年級學生。

6 教學過程

6.1 案例呈現

如下一個數學問題：

已知：f（x）=ax2-c, 且 -4≤f（1）≤-1,-1≤f（2）≤5

求：f（3）的取值范圍。

有相當一部分同學求解如下：

（設計意圖：學生用認知結構中已有的舊知識去解決新問題時，學生往往缺乏聯系和學習的積極主動性，教師采用角色換位的解題教學方法，使學生親身經歷解題的過程，讓學生產生認識沖突，激發學生探知的強烈欲望，對問題進行“理解”與“消化”達到數學信息多角度的表征。）

6.2 解題策略指導

教學中，該問題（學生的解題思維過程）提出來，供大家討論，同學們學習興趣十分高漲，這時，采取對學生積極引導并提出如下質疑：（1）上述問題推理過程是否正確？其推理理論依據是什么？（2）其思維過程是否為等價轉化？（3）請你用嘗試方式驗證結論的極端值是否正確。（4）綜上分析，你的最終結論是什么？

學生一般都經歷先認為原解法正確再否認的思維過程。其主要思維體現如下：對于引導①，由于理論明顯，都歸因于不等式的性質。對于引導②，由于暫時性地無法發現錯誤，很多同學都認為過程為等價變形。待引導③出現之后，大部分學生思維開始又活躍起來。他們積極從如下思考：

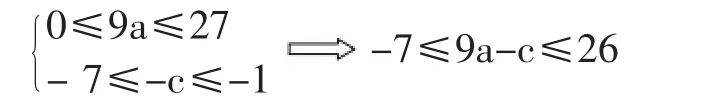
當 f（3）=26 時，當且僅當 9a=27,-c=-1

此時 a=3，c=1 從而 f（1）=a－c=2∈[-4,-1]

f（2）=4a-c=11∈[-1,5]

與條件矛盾，可見f（3）不可能到26

當 f（3）=-7 時，當且僅當 9a=0,-c=-7

此時 a=0，c=7，從而 f（1）=a-c=-7 ∈[-4,-1]

f（2）=4a-c=-7∈[-1,5]

也與條件矛盾，可見f（3）也不可能到-7

至此，大家一致認為解答有誤，可原因在哪兒呢？

（設計意圖：實現學習活動及其構成也不是單純的個人的進程，而是在于師生、學生間的共同活動，包括一起分析并尋找聯系與解答，一起設計與證明，還一起檢驗與評估其結果，以此創設一個好的“學習共同體”。）

6.3 協作研究探索

通過上述的分析，大家質疑“不等式性質定理3的推論”在解題中使用造成的嗎？故師生進入了對不等式的可加性做進一步的思考與分析。

結果發現：定理3的推論：若a>b，c>d則a+c>b+d中，條件“ a>b，c>d”是“ a+c>b+d”成立的充分不必要條件。

本題中，解題思維過程的蘊涵關系如下：

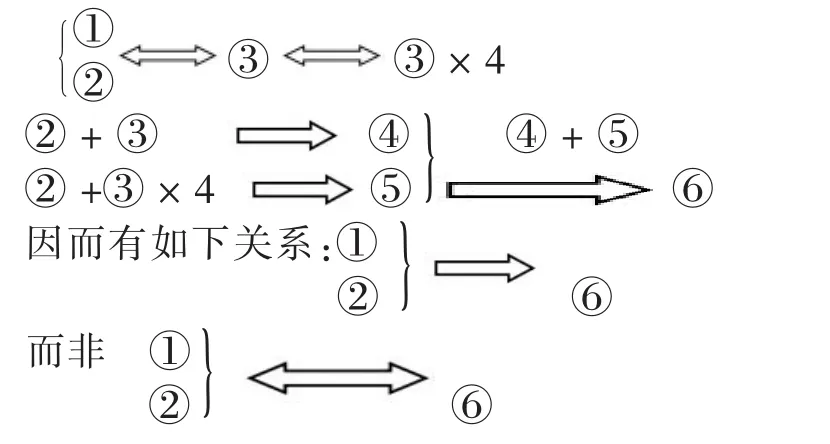
案例中所依據的理論是正確的，但由于違背了等價性的思想和原則，卻將問題的范圍擴大了。即上述推理雖然得出 f（3）∈[-7，26]，但卻不能取滿到-7 到 26 之間的一切值。

（設計意圖：通過對數學思維過程的分析與思考，加深了學生對數學概念理解，滲透了等價轉化的思想方法，達到了實現認識整合，打破認識平衡狀態的目的。）

6.4 意義建構，解決問題

我們的問題可以等價地轉化為：

求 f（3）=9a-c 的取值范圍。

解：設M=9a-c，從而 c=9a-M

故問題又等價轉化為：過圖象中的區域內EFGH的點（a,c），作斜率為9的直線，求其在c軸上的載距-M的取值范圍。

顯然，當過點 E（0,1），即 a=0,c=1時 -M 有最大值 1，當過點 G（3,7），即 a=3,c=7 時，-M 有最小值-20。

即有：-20≤-M≤1

∴-1≤M≤20

故所求 f（3）的取值范圍為[-1,20]

（注：這里滲透了線性規劃的思想和方法）

另解：令 m（a-c）+n（4a-c）=9a-c

用待定系數法，得

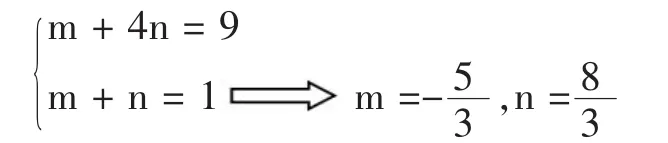
①×（-5/3）+②×8/3 得 -1 ≤ 9a-c≤ 20

∴所求范圍是[-1,20]

（設計意圖：循尋學生心理認識發展的規律，在學生認識經歷了“平衡—不平衡”的發展變化之后，不失時機地向學生介紹正確的解題方法與技巧，同化學生的心理認識結構，達到認識的新平衡狀態，順利實現學生對新知識的心理意義建構。）

一種獨立的教學模式構建，必須通過對教學模式的長期實踐，筆者僅對數學解題模式做出上述初步構建，以期隨著建構主義理論的深入學習與后繼的教學研究實踐使之完善。