多機理下的衛星壽命預測方法與應用

，，

北京空間飛行器總體設計部，北京 100094

衛星是由專用有效載荷、姿態與軌道控制、結構與機構、熱控、電源和測控等多個分系統組成的復雜系統，絕大多數衛星具有一次發射、長期使用的特點。衛星在軌服務過程中，其剩余壽命直接影響到衛星規定壽命要求滿足的程度和壽命末期的處置策略，尤其對于衛星星座而言，衛星剩余壽命直接影響星座維持與補網計劃，關系到星座可用性和連續穩定運行的能力。因此，預測衛星壽命并盡可能提高結果的可信度在工程中具有重要意義。

當前，有關衛星產品的壽命預測研究主要集中在部組件層次，一般是針對具有退化或漸變規律的產品，例如蓄電池、推力器、驅動機構等，提出某一產品的壽命預測方法[1-9]。而由于衛星系統的復雜性，整星的壽命預測研究非常少，現有方法主要是通過估算剩余推進劑來預測衛星剩余壽命[10-13]，這類方法沒有考慮衛星突發故障和退化失效的情況，其應用有固有的局限性。

根據國內外衛星在軌故障統計[14-16]，衛星壽命終結不僅和燃料耗盡有關，也和隨機失效、退化失效有關。因此，準確的壽命預測應完整考慮突發故障、退化和消耗多種因素，并反映這些因素尤其是突發故障導致的在軌壽命分布的動態變化。本文針對衛星壽命預測的現實需求和以往方法的不足，針對隨機失效提出了隨單星工作時間和系統結構變化的剩余壽命預測模型，并綜合隨機失效、退化、消耗及其在軌變化規律，給出了多機理下的整星壽命預測方法。這一方法既可用于單星剩余壽命預測，也可用于星座備份星替換策略的制定。

1 衛星壽命與失效的特征

1.1 星上產品的壽命特征及衛星到壽原因分析

按照失效機理不同，星上產品的壽命特征一般可分為以下3類：

1)隨機壽命類，即產品壽命服從隨機失效分布，可能很快發生在軌故障并永久失效，也可能長期正常運行并遠遠超過設計壽命。星上多數產品可歸為這一類，例如通用電子產品。

2)退化壽命類，即產品特性服從特定的退化規律并在可預見的時間范圍內必然達到壽命，例如蓄電池、太陽電池陣、行波管等。

3)消耗壽命類，一般是指推進劑等消耗性物質，當消耗到規定閾值時，產品到壽。

此外，某些產品的壽命可能具有多種特征，例如行波管放大器既有退化失效也有隨機失效，銣鐘既有消耗壽命也有隨機失效等。這類產品在處理時需要分析多種機理。

根據星上產品的壽命特征和國內外衛星故障情況[14-16]，衛星長期在軌工作過程中，壽命終結的原因一般包括：

1)由于突發故障導致整星失效。這類故障的發生具有隨機性，故障產品在失效前的長期工作中沒有明顯的性能變化，往往在某種誘因下突然失效。例如2003年2月，泰國通信衛星-3在發射5年10個月后，由于電源系統短路造成整星失效；2000年3月，ERS-1衛星發生姿態控制故障導致任務失敗,服役結束。在沒有其他類型故障和消耗性物質足夠的前提下，衛星實際運行時間可能遠超出其設計壽命。

2)由于消耗性物質用盡導致衛星到壽。例如星上剩余推進劑達到規定值，衛星不得不進行離軌操作或直接退役。這種情況下衛星并未發生故障，通常已經超過規定的工作壽命要求。

3)由于產品性能退化到不可接受的程度導致衛星到壽。典型情況例如太陽電池陣效率下降導致整星功率不足、行波管增益下降導致射頻通道失效等。

1.2 衛星隨機失效分布的特點

由于退化壽命和消耗壽命具有相對確定性，有關產品的設計壽命一般留有足夠余量，因此在衛星系統可靠性分析中，通常僅分析隨機失效。

衛星系統可靠度一般根據設備或分系統可靠性預計值利用系統可靠性模型計算得到。由于衛星大量采用冗余設計，典型的系統可靠性曲線如圖1所示，這一曲線可以擬合為威布爾分布。

由于指數分布具有“無記憶性”，即產品的工作壽命和產品已工作多長時間無關，這在處理很多工程問題時具有極大的方便性。因此，也可假設衛星服從指數分布，此時衛星的失效率：

(1)

式中：λs為衛星失效率；Ts為衛星的規定壽命，R(Ts)為根據衛星系統可靠性模型計算得到的規定壽命的可靠度。衛星指數分布如圖1所示。

由圖1可見，在規定壽命期內，衛星采用指數分布是偏保守的。從國內外經驗看，衛星隨機失效通常取威布爾分布，并在很多情況下為了處理的方便，假設服從指數分布[17-18]。

2 隨機、退化和消耗壽命的分析方法

2.1 基于隨機失效的衛星剩余壽命

盡管星上設備種類很多，但如前文所述，根據系統可靠性模型最終可以近似得到一個整星隨機壽命分布。利用這一分布，通過蒙特卡羅仿真可以得到基于隨機失效的衛星剩余壽命。但這一過程中有兩個關鍵問題：

1)衛星在軌時間是持續增加的，但仿真產生的隨機失效時間可能小于衛星在軌時間。因此，需要剔除衛星已工作時間的影響。

2)隨機失效產品可能在任意時刻發生故障。常見的情況是某設備故障使系統冗余度降低，衛星系統可靠性模型和失效分布參數也相應變化。因此，需要考慮隨機失效分布的動態特性。

針對第1個問題，不失一般性，假設衛星已工作時間為T0，仿真產生的隨機失效時間為T1，則T1必須大于T0才是一次有效仿真。當T1>T0時，衛星一次仿真中隨機壽命Tr的實際值為：

Tr=T1-T0

(2)

式中：Tr、T0、T1的時間單位均為h。

針對第2個問題，當衛星未發生常駐故障、系統可靠性模型不變時，T1可以根據衛星初始壽命分布仿真得到。若衛星服從指數分布且其失效率為λ0，則衛星隨機失效時間的仿真值為：

(3)

式中：η為隨機數，0<η<1。

若衛星服從威布爾分布且當前的概率密度函數為：

(4)

式中：b為特征壽命，c為形狀參數。則衛星隨機失效時間的仿真值為：

(5)

假設衛星于T1a時刻某單機主份故障，系統組成變化如圖2、圖3所示。

由圖3可知，衛星系統冗余度降低，系統可靠性模型改變，分別考慮指數分布和威布爾分布兩種情況如下。

(1)指數分布情況

當衛星發生故障后，可以根據新的可靠性模型計算得到新的可靠度R1(Ts)，根據式(1)可得到新的失效率λ1，基于指數分布的“無記憶性”，以λ1代入式(3)求得隨機失效時間值即可。

(2)威布爾分布情況

根據新的可靠性模型可擬合得到新的威布爾分布參數，此時衛星壽命分布呈現兩階段分布特征：

(6)

式中：ba、ca為衛星在T1a時刻前的威布爾分布參數；bb、cb為衛星在T1a時刻后的威布爾分布參數，根據新的可靠性模型擬合得到；T0b為第二階段威布爾分布的位置參數，基于衛星壽命分布的連續性：

(7)

邏輯上有T0>T1a，因此，衛星隨機失效時間的有效仿真值應為：

(8)

當衛星于T1b時刻再次發生常駐故障、系統可靠性模型變化時，衛星壽命分布將呈現三階段分布特征，其分布形式和有效仿真值在式(6)、式(8)基礎上依次類推。

2.2 基于消耗性物資的衛星剩余壽命

大多數衛星的消耗壽命僅取決于推進劑。考慮更一般的情況，假設有m種影響衛星壽命的獨立消耗因素，則衛星消耗壽命取決于消耗最快的因素，有:

Tc=min(T21,T22,…,T2m)

(9)

式中：T2i(i=1,2,…,m)是第i種消耗因素的預估壽命，根據每種消耗因素的壽命模型計算而得。

以推進劑消耗為例，假設利用現有技術[8]預估的衛星當前剩余推進劑為X，衛星年消耗推進劑為X1～X2，衛星不可使用的推進劑殘留量、離軌再捕獲推進劑消耗量和計算誤差量之和為Xr。并假設推進劑年消耗量呈均勻分布，根據均勻分布的蒙特卡羅抽樣公式，由推進劑決定的衛星消耗壽命為：

T2=[T2a+η(T2b-T2a)]×8 760

(10)

式中：T2a=(X-Xr)/X2；T2b=(X-Xr)/X1。

2.3 基于退化失效的衛星剩余壽命

假設有n種影響衛星壽命的獨立退化失效因素，則在一次仿真中，衛星退化壽命取決于退化最快的因素，有：

Td=min(T31,T32,…,T3n)

(11)

式中：T3i(i=1,2,…,n)為第i種退化失效的預估壽命，根據每種退化模型計算而得。

以太陽電池陣功率衰減為例，假設當前功率為P，年衰減率為Y1～Y2，衛星正常功率需求為P0。并假設太陽電池陣衰減率可按均勻分布處理，則由太陽電池陣衰減決定的衛星剩余壽命為：

T3=[T3a+η(T3b-T3a)]×8760

(12)

式中：T3a=(P-P0)/PY2；T3b=(P-P0)/

PY1。

3 衛星剩余壽命的仿真分析

3.1 分析約定

(1)整星壽命預測覆蓋的產品范圍

如前所述，衛星由退化、消耗和隨機失效三類壽命特征產品組成，僅考慮其中任何一類產品都是不完整的，因此整星壽命預測不僅應考慮推進劑等消耗性物資，以及太陽電池陣、蓄電池組等產品的退化，還應考慮衛星任務相關的所有分系統和設備，包括有效載荷和平臺的電子產品、機電產品、活動部件等各類產品的突發故障。

(2)復雜失效機理產品的處理

某些產品同時存在多種失效機理，例如蓄電池組既有可能由于電路缺陷突發故障，也可能由于性能衰降而失效。當沒有占主導地位的失效機理時，應同時考慮多種失效機理，例如蓄電池組需同時考慮隨機失效和退化失效，在分析時引入指數分布和退化模型。

(3)隨機失效分布的選擇

衛星隨機失效一般可用威布爾分布或指數分布描述，威布爾分布的分析結果一般更準確，適用于單星剩余壽命預測等對準確度要求較高的情況，指數分布的分析過程則更簡單，可用于多星星座的備份星策略等對單星隨機壽命敏感性不高的情況。

3.2 多機理下的衛星壽命模型

依據衛星組成與產品壽命特征，可全面梳理影響衛星壽命的因素，并按消耗、退化、隨機失效分為三類，建立樹圖如圖4所示。

由圖4可見，在系統層面衛星壽命模型體現為“或門”形式的競爭模型。在底層單元建模中，每一種消耗或退化失效因素應作為獨立單元列出。隨機壽命模型可以系統級可靠性模型為基礎，通過去除退化單元、僅保留隨機失效單元建立，通常包括各類電子設備和以指數分布/威布爾分布表征的機電設備、推進組件等。

如第1.2節所述，在整星層面可以將隨機失效擬合為威布爾分布模型或指數分布模型。由此，假設衛星隨機失效決定的剩余壽命為Tr，m種消耗因素決定的剩余壽命為T2i(i=1,2,…,m)，n種退化失效決定的剩余壽命為T3i(i=1,2,…,n)，則衛星剩余壽命為

Tleft= min[Tr,min(T21,T22,…,T2m),

min(T31,T32,…,T3n)]

(13)

3.3 仿真分析流程

在已知隨機失效各單元壽命模型、消耗和退化規律的前提下，可以利用蒙特卡羅仿真方法進行衛星壽命預測，其仿真流程如圖5所示。具體流程說明如下。

(1)設置初始條件

初始條件包括各單元壽命模型的參數值、衛星預期運行時間、仿真次數等。

(2)預估隨機失效決定的剩余壽命

依據衛星當前所服從的隨機失效模型，利用蒙特卡羅仿真抽樣公式，產生衛星隨機失效時間T1，若T1大于衛星已工作時間T0，則根據式(2)

得到該次仿真中由隨機失效決定的剩余壽命Tr；若T1≤T0，則本次仿真無效，直接進入下一次仿真，再次產生T1的值。

(3)預估消耗性物質決定的剩余壽命

根據消耗性物質的消耗規律，獲取每一種消耗因素的剩余壽命T2i(i=1,2,…,m)，比較并取其最小值即得到一次仿真中的消耗剩余壽命Tc。

(4)預估退化失效決定的剩余壽命

根據各種退化因素的退化規律，獲取每一種退化因素的剩余壽命T3i(i=1,2,…,n)，比較并取其最小值即得到一次仿真中的消耗剩余壽命Td。

(5)確定一次仿真中的衛星剩余壽命Tleft

根據基于競爭模型的衛星剩余壽命式(13)，比較并取Tr、Tc、Td中的最小值即得到衛星在一次仿真中的剩余壽命Tleft。

重復流程(2)～(5)，進行多次仿真后，可得到有效仿真次數Ne和Ne個衛星剩余壽命值，則衛星平均剩余壽命為:

(14)

(7)計算衛星剩余壽命分布

衛星隨機失效、退化失效及消耗均存在一定的不確定性，因此衛星剩余壽命的預估結果存在置信度。為了描述這一不確定性，給定統計區間間隔，統計落在每一個區間內的衛星累積到壽次數，即可得到衛星剩余壽命分布。

首先設置統計區間間隔(例如30天)，根據當前時刻至給定日期的時間區間求出統計區間數量NΔ：

NΔ=Tab/TΔ

(15)

式中：TΔ為統計區間間隔；Tab為當前日歷時間至給定日期的時間區間。

然后統計落在每一個統計區間內的衛星累積到壽次數Fi，則衛星剩余壽命服從：

PT=1-Fi/Ne,i=1,2,…,NΔ

(16)

式中：PT即衛星剩余壽命為T的概率。

4 應用示例

已知某星座由6顆衛星構成，衛星設計壽命7年，部分衛星已經接近更新換代。為盡早確定備份星計劃，需要預測在軌衛星剩余壽命并評估其超期服役的可能性。假設衛星隨機失效服從指數分布，消耗性因素為推進劑，推進劑年消耗量為3～5 kg，退化因素為電池陣功率衰減，衛星功率需求不低于500 W，其他信息如表1所示。

由表1可見，盡管衛星固有設計一致，但隨著在軌工作時間增加，各顆衛星在系統有效配置、推進劑消耗和退化情況上均出現差異。根據表1數據和本文方法，經計算得到各星預估壽命如表2所示。衛星剩余壽命分布如圖6所示。

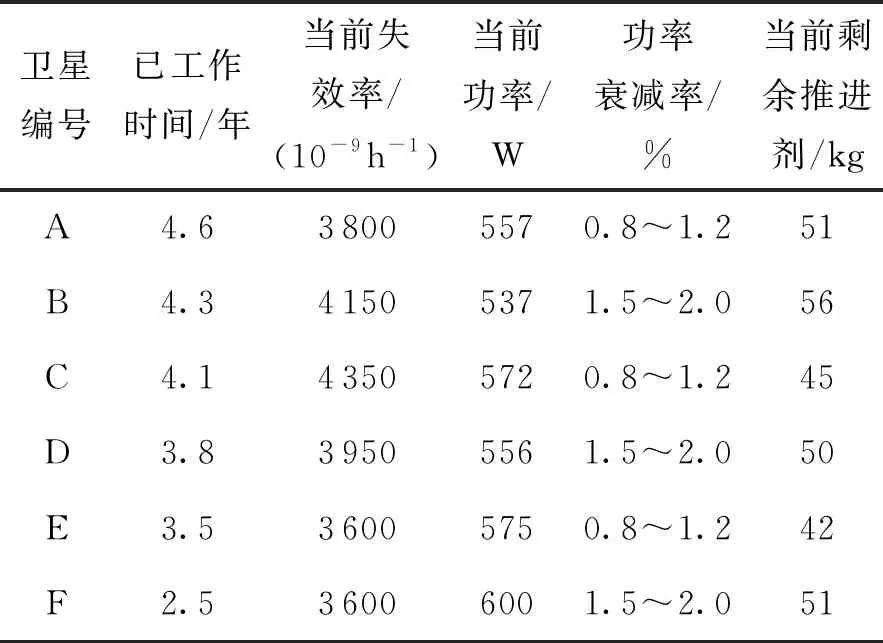
表1 衛星壽命模型有關數據

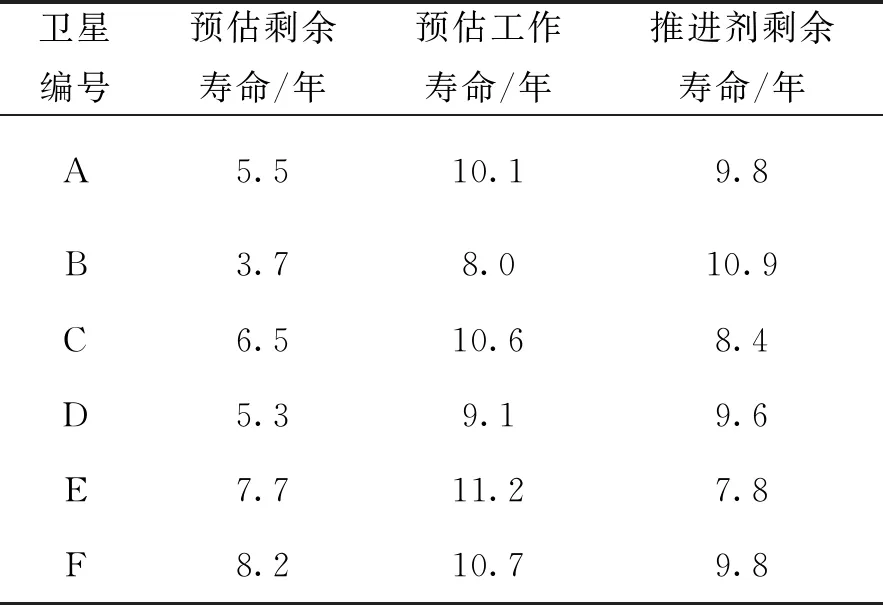
表2 預估的衛星剩余壽命(均值)

由表2、圖6可見，盡管B星剩余推進劑較多、D星發射時間較晚，但這兩顆衛星的剩余壽命最短，是維持星座平穩運行的薄弱環節，需提前制定替換計劃；衛星剩余壽命和發射時間無必然聯系，但和衛星在軌運行情況密切相關。

本文方法和基于推進劑估算方法的分析結果對比如圖7所示。

由圖7可見，基于剩余推進劑估算方法得到的結果均高于本文方法；個別衛星預估結果差異較大，尤其是B星，僅估算剩余推進劑時，其剩余壽命超過10年，但綜合考慮星上系統工作狀態、退化情況和燃料消耗，其剩余壽命均值不超過4年，顯然，基于剩余推進劑估算的方法獲得的結果過于樂觀。

5 結束語

衛星在軌壽命終結是隨機失效(突發故障)、退化失效和物資消耗三種機理作用的結果。分析衛星壽命特征，利用多機理下的壽命預測方法通過案例分析表明：

1)僅利用推進劑估算衛星剩余壽命可能得到過于樂觀的結果。準確的壽命預測應覆蓋隨機失效、退化和消耗三類因素。

2)多機理下的壽命預測方法理論上具有更高的可信性，更適用于星座備份策略分析等工程應用。

通過多星組網運行提供連續服務是通信、導航、遙感等業務的重要實現途徑。與單星任務不同，星座通常具有補網需求，準確預估衛星壽命對于星座維持和補網策略的制定具有重要意義。為獲得更精確的分析結果，在各類設備的壽命變化規律和整星壽命模型等方面，仍需要開展大量研究工作。