淺析創(chuàng)新教育在初中數(shù)學(xué)課堂教學(xué)中的應(yīng)用

余佳

摘要：創(chuàng)新教育是以培養(yǎng)人的創(chuàng)新精神和創(chuàng)新能力為基本價值取向的教育。本文從創(chuàng)新教育的基礎(chǔ)入手，對創(chuàng)新教育在數(shù)學(xué)課堂中作出一些初探。本文認(rèn)為，首先要將提升學(xué)生的思維品質(zhì)貫穿于數(shù)學(xué)教學(xué)實踐中，其次要注意創(chuàng)新教育在數(shù)學(xué)課堂中的策略。

關(guān)鍵詞：創(chuàng)新教育；數(shù)學(xué)思維；教學(xué)策略

中圖分類號：G633.6 文獻(xiàn)標(biāo)識碼：A 文章編號：1992-7711（2018）03-0036

一、對創(chuàng)新教育的理解

1. 創(chuàng)新教育的發(fā)展背景

隨著知識、信息化時代的到來，對創(chuàng)新人才的需求越來越高。創(chuàng)新教育是素質(zhì)教育的重要內(nèi)容，隨著我國新課程改革的不斷深化，創(chuàng)新教育已經(jīng)被提升到教育教學(xué)的重要位置。

2. 創(chuàng)新教育的幾層涵義

創(chuàng)新教育是貫徹教育新理念的航標(biāo)；創(chuàng)新教育是教育創(chuàng)新的前提；著重提升學(xué)生的創(chuàng)造能力是創(chuàng)新教育的宗旨。

二、將提升學(xué)生的思維品質(zhì)貫穿于數(shù)學(xué)教學(xué)實踐中

1. 積極調(diào)動學(xué)生開動腦筋的積極性，鍛煉學(xué)生的思維能力

要結(jié)合數(shù)學(xué)學(xué)科性質(zhì)，挖掘?qū)W生的思維潛力，使學(xué)生的思維具有開放性，在面對復(fù)雜問題時能夠從不同的途徑進(jìn)行解決，培養(yǎng)學(xué)生學(xué)會多種數(shù)學(xué)思維方式，在具體的學(xué)習(xí)實踐中能夠綜合運用比較法、歸納演繹法，會分類、會總結(jié)等綜合能力。

2. 要讓學(xué)生學(xué)會提問，并具有質(zhì)疑精神

提出問題的能力遠(yuǎn)比解決問題的能力更重要，讓學(xué)生學(xué)會提問題是對學(xué)生進(jìn)行創(chuàng)新能力培養(yǎng)的前提基礎(chǔ)。學(xué)生由于受自身經(jīng)驗對理解水平的限制，很難對教材內(nèi)容做到直觀化理解。由于學(xué)生對教材內(nèi)容不熟悉、不理解，因此很難提出有價值的問題。為此，教師一定要結(jié)合學(xué)生比較熟悉的環(huán)境或事物來創(chuàng)設(shè)教學(xué)情境，充分挖掘?qū)W生的認(rèn)知經(jīng)驗，讓學(xué)生在此基礎(chǔ)上進(jìn)行提問。

3. 針對問題，提升學(xué)生的假設(shè)能力

提出假設(shè)，有助于學(xué)生借助以往的經(jīng)驗知識對問題進(jìn)行探究，有助于提升學(xué)生的思維能力。在初中數(shù)學(xué)教學(xué)中，培養(yǎng)學(xué)生對問題的假設(shè)能力，是一種有效的教學(xué)途徑。

三、創(chuàng)新教育在數(shù)學(xué)教學(xué)實踐中的策略

1. 讓學(xué)生從根本上把握數(shù)學(xué)的本質(zhì)，并將其運用在實踐中

學(xué)生要想從根本上把握數(shù)學(xué)本質(zhì)，就要從數(shù)學(xué)概念、數(shù)學(xué)思維、數(shù)學(xué)美感、數(shù)學(xué)精神、數(shù)學(xué)方法等角度入手。要以學(xué)生的實際發(fā)展水平為創(chuàng)新教育實施的依據(jù)，讓學(xué)生在原有知識、原有經(jīng)驗與能力水平的基礎(chǔ)上，進(jìn)行新知識的探索與研究，讓學(xué)生能從數(shù)量與空間關(guān)系的處理中，學(xué)會透過現(xiàn)象看本質(zhì)，能夠從感性認(rèn)識上升到理性認(rèn)識，進(jìn)而提升自我的創(chuàng)新力。

例如，在“線段的比較”一節(jié)教學(xué)中，先讓兩名學(xué)生到臺前演示、比較身高，找學(xué)生說出比較的方法，歸納出幾個要點，然后再引導(dǎo)學(xué)生建立比較兩條線段大小的模型，找出其中的三要素，從而很容易理解疊合比較法的原理。為了講度量比較法，我問學(xué)生：你們是否和外地親戚家的同齡小朋友談起過誰高誰矮的問題？從而使學(xué)生聯(lián)想到互報身高加以比較的情境，進(jìn)而很容易地找到了線段的第二種比較法。切合學(xué)生的日常生活，不僅能夠調(diào)動學(xué)生的興趣，也增強了課堂活力。

2. 注意拓展知識的空間

數(shù)學(xué)教材內(nèi)容雖然都是經(jīng)過認(rèn)真鉆研與精心設(shè)計而成的，但是受多種因素的影響，數(shù)學(xué)教材具有簡練概括的特性。教學(xué)時，不一定按照教材編排按部就班地進(jìn)行，可以將一個知識的空間加以拓展，使學(xué)生的思維得到充分的發(fā)展。

例如，在“勾股定理”一節(jié)教學(xué)中，除了書上的證明方法之外，還可以讓學(xué)生多嘗試一些其他證明方法，這不僅能使該知識得到強化，也能使學(xué)生認(rèn)識到各種方法的科學(xué)性、合理性。

3. 動手操作，培養(yǎng)創(chuàng)新能力

實踐是檢驗真理的唯一標(biāo)準(zhǔn)，學(xué)生只有將所學(xué)知識真正在實踐中自如應(yīng)用，進(jìn)而實現(xiàn)知識的真正價值，因此在數(shù)學(xué)教學(xué)中要著重鍛煉學(xué)生的知識實踐能力，如此才會為創(chuàng)新教育打下堅實的基礎(chǔ)。

例如，在“四邊形”一章教學(xué)中，讓學(xué)生制作出一般的四邊形、平行四邊形、菱形、矩形、正方形的紙板模型，讓學(xué)生在操作中建立起它們之間的聯(lián)系與區(qū)別，通過觀察、測量，得出它們的性質(zhì)，使學(xué)生學(xué)習(xí)這些知識不再枯燥，以提升學(xué)生學(xué)習(xí)的興趣。

4. 為教學(xué)創(chuàng)設(shè)恰當(dāng)?shù)那榫常瑢W(xué)生進(jìn)行啟發(fā)

學(xué)會提問，才會學(xué)會學(xué)習(xí)，為此教師要有意識地去培養(yǎng)學(xué)生的提問能力。在這一方面，啟發(fā)式教學(xué)是一個有效途徑。學(xué)生通過提問，會抓住問題的實質(zhì)，有利于深入到問題的內(nèi)部，進(jìn)而更易于從本質(zhì)上理解問題，并且會在頭腦中形成規(guī)律，易于對問題進(jìn)行類型化掌握。問題的解決，會給學(xué)生帶來成功的喜悅，這種思維上的成功，會進(jìn)一步促進(jìn)學(xué)生創(chuàng)新能力的發(fā)展，更利于充分挖掘?qū)W生的思維潛能。

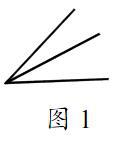
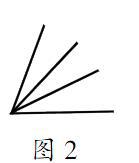
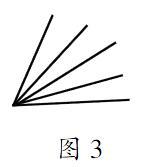
例如，在“識角”教學(xué)中，圖1有多少個角？圖2呢？圖3呢？

學(xué)生能逐一回答，此時提問：如果中間有99條射線，能有多少個角？這一問題大大激發(fā)了學(xué)生的興趣，大部分學(xué)生的看法是1，2，3，……地數(shù)下去，這是不科學(xué)的，能否找出一個計算公式呢？通過問題引入，最后培養(yǎng)學(xué)生的發(fā)現(xiàn)能力。

5. 解除思維定勢對學(xué)生思維的限制

思維定勢是指學(xué)生面臨已經(jīng)變化的新問題，知識的趨向性使學(xué)生無意識地將自己的思維活動局限在解決問題的固定模式中，或把并非一般性的局部經(jīng)驗不由自主地歸類到一般范圍或形同實異場合應(yīng)用，最終導(dǎo)致負(fù)面結(jié)果。

總之，從創(chuàng)新教育到教育創(chuàng)新是一個艱苦的歷程，教師只有從觀念上做到重視，并貫穿運用在教學(xué)實踐過程中，就一定會取得成效。

（作者單位：貴州省仁懷市第八中學(xué) 564500）