一種魯棒的室內定位優化算法*

徐 琨， 劉宏立， 詹 杰， 馬子驥

(1.湖南機電職業技術學院 電氣工程學院，湖南 長沙 410151；2.湖南大學 電氣與信息工程學院，湖南 長沙 410082； 3.湖南科技大學 物理與電子科學學院，湖南 湘潭 411201)

0 引 言

節點定位[1]是無線傳感器網絡[2](wireless sensor networks，WSNs)的關鍵技術，準確地知道節點的位置信息有助于地理路由[3]、時空信息傳播[4]和協同信號處理[5]。目前，接收信號強度指示[6](received signal strength indication，RSSI)、到達角度[7](angle of arrival，AOA)、到達時間[8](time of arrival，TOA)和到達時間差[9](time difference of arrival，TDOA)是最常用的定位技術。其中，基于RSSI的定位技術由于實現簡單、無需增加額外的硬件設施，近幾年一直是研究熱點[10]。文獻[11]利用移動節點緩解室內環境中RSSI的不穩定性，提出了一種自適應定位算法。文獻[12]通過提前建立RSSI與距離之間的映射關系，提出一種基于位置指紋的定位算法。文獻[13]將定位問題轉換為最大似然(maximum likelihood，ML)估計問題，采用迭代的算法求出目標節點的位置信息。文獻[14]考慮最小化測量距離和真實距離之間的殘差，將定位問題轉換為最小二乘(least squares，LS)問題，采用線性逼近的方法進行求解。目前提出的大部分算法均假設已經提前知道所有錨節點的發射功率值，且假設所有節點的發射功率相同，很少有文獻考慮發射功率未知和發射功率不同的情況。

傳感節點一般會隨機部署在監測區域中，由于網絡配置和節點硬件設施的原因，很難精確預知每個節點的發射功率大小。即使在網絡部署之初為每個節點都設置相同的發射功率值，但隨著節點電量的損耗、新節點的加入，每個節點的發射功率值都會發生變化。

本文提出了一種魯棒的、無需預知發射功率大小的定位優化算法。該算法考慮節點發射功率未知的情況，將發射功率看成一個未知的變量參與到節點的定位過程中，利用線性逼近的方法將一個非線性的定位問題轉換為簡單的線性問題，并用LSM計算未知節點的坐標。實測實驗和仿真證明提出算法具有很好的定位性能。

1 網絡系統模型

考慮一個由N個錨節點和1個目標節點組成的傳感網絡，每個錨節點的位置已知，xi=[xi,yi],i=1,2,…,N。目標節點隨機部署在網絡中，其位置未知，x=[x,y]。目標節點向網絡中發出定位請求，鄰近的錨節點接收到對應的定位請求后給目標節點發送一個信標報文，信標報文中包括錨節點的ID和對應的位置信息，錨節點的發送功率大小未知。基于對數—正態路徑衰減模型，目標節點x接收第i個錨節點xi的接收信號強度可以表示為

Pi=p0-10nPlg(di/d0)+mi,i=1,2,…,N

(1)

由式(1)可以看出，為了得到錨節點和目標節點之間的距離估計值，需要估算出參數P0的值，其對應的ML估計函數可以表示為

(2)

式(2)表示一個非線性非凸的優化問題，且存在多個未知參數，求出對應的最優解是一件非常困難的問題，具有很高的計算復雜度。

2 魯棒的室內定位算法

采用線性逼近的方法將節點定位問題規范化為一個線性優化問題，很容易求出式(2)對應的全局最優解。由于參數P0未知，針對給出的系統模型，需要將式(1)中的功率P0看成一個未知參數參與對目標節點的定位。為了求出目標節點的坐標，首先對式(1)的兩邊進行移項, 并對等式的兩邊同時除以10np有

(3)

為了消除式(4)中的對數項，采用一系列的數學運算和變形，有

(4)

(5)

用向量形式可以表示為

(6)

采用LSM，可以求出未知變量的解，得出目標節點的未知坐標為LS=(ATA)-1ATB。

3 仿真與性能分析

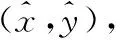
3.1 仿 真

采用MATLAB進行仿真，所有仿真實驗都在一臺CPU為Intel Core i5、主頻為3 GHz，內存大小為4 GB,1 600 MHz DDR3的臺式機上進行。在一個20 m×20 m的區域內隨機部署20個錨節點，目標節點隨機的部署在測試區域內。為了減少測距誤差對定位性能的影響，對每個算法的仿真運行100次。在仿真過程中，為了真實地反映實際的測試環境，對所有的RSSI信號添加均值為0，標準差為0.5的高斯隨機噪聲。仿真時設置發射功率P0在區間[-55，-25]dBm 之間進行選擇。

發射功率未知時不同算法的定位性能如圖1所示。傳統的ML算法和LSM都假設已經提前預知發射功率大小，其值為-35 dBm。當真實發射功率和提前預知的發射功率相差不大時，提出算法和傳統的定位算法具有相似的定位性能。但隨著預知的發射功率和真實發射功率的差異變大，提出算法明顯優于傳統的定位算法，這是因為本文算法將發射功率作為一個未知參數參與定位，而傳統的算法采用錯誤的發射功率值，其測距將存在嚴重的誤差，且隨著功率間的差異變大，測距誤差會急劇增大，從而嚴重降低傳統算法的定位性能。

圖2為2個錨節點發射功率未知時，不同定位算法的定位性能。在仿真時，有2個錨節點的發射功率隨機選擇，其他錨節點的發射功率統一設置為-35 dBm。從圖中可以看出，本文算法的定位性能要明顯優于傳統的定位算法，因為傳統的定位算法假設所有的發射功率都相同，而提出算法將發射功率看成一個未知參數，可以有效地減少發射功率未知對定位的影響。當參與定位的信標節點越來越多時，3種算法的定位性能均得到了改善。

圖1 不同算法在未知功率下的定位誤差

圖2 不同定位算法在存在2個未知功率節點時的定位誤差

3.2 實測實驗

在大小為5.9 m×3.7 m的實驗室進行了實測實驗，實驗中的目標節點和錨節點均采用CC2430的通信模塊，其對應的工作頻率為2.4 GHz，發送和接收天線都采用1/4波長的全向天線。測試區域中存在電腦、實驗桌、空調等物品，在房間內部署6個錨節點和1個目標節點，節點之間通過ZigBee協議組成自組網絡實現相互通信。每次實驗時均給錨節點設置不同的發射功率，并記錄不同發射功率下，距離1 m時的接收功率值，測試結果為當發射功率Pt分別為0，-1，-3，-5，-7，-10，-15 dBm時，對應的平均接收功率P0分別為-37.24，-38.68，-39.5，-41.56，-44.17，-46.47，-53.74 dBm。

室內環境下不同算法的定位性能如圖3所示。對于室內測試環境，仍然假設ML算法和LSM已經預知發射功率大小，其值為-35 dBm。從圖中可以看出，由于本文算法考慮了發射功率未知的情況，其對應的定位性能明顯優于傳統的ML和LSM。隨著預知功率值和真實功率值的差異變大，2種傳統定位算法的誤差快速增大，而本文算法依然具有很好的定位性能。通過和圖1中的仿真結果進行比較，發現在真實的室內環境中所有算法的定位性能要比仿真環境中的定位性能差。這是因為在真實的室內環境中，信號受障礙物的反射、折射等的影響，其RSSI值的變化要明顯大于仿真中RSSI值的變化。

圖3 室內環境下不同算法在未知功率的定位誤差

4 結 論

提出了一種魯棒的定位算法，仿真和實驗證明提出算法在發射功率未知時亦能提供很好的定位性能，其定位性能要明顯優于傳統的ML和LSM。