一種新型Ka波段衛星信號抗截獲調制方案*

張 喆， 達新宇， 劉慧軍

(空軍工程大學 信息與導航學院，陜西 西安 710077)

0 引 言

由于軍事通信較高的安全需求，Ka波段衛星投入應用，需要一種可靠的抗截獲調制方案來保證信號安全傳輸。當前衛星信號安全傳輸相關研究主要集中在基于密碼學的信號加密與物理層安全方面，其中加權類分數階傅里葉變換(weighted-type fractional Fourier transform,WFRFT)是一種新型物理層安全手段，具有物理結構簡單、信號隱蔽性強的特征，有很大的發展潛力。

文獻[1]提出離散WFRFT定義，并論證其構成通信系統的可行性;WFRFT處理后的基帶信號星座圖分布具有類高斯性，故能起到抗截獲功能[2]；梅林通過對WFRFT的誤碼率分析得出其參數具有抗截獲性能；Li T對雙層加權類分數階傅里葉變換(double-layer weighted-type fractional Fourier transform,DL-WFRFT)的基帶信號進行研究時，通過觀察星座圖分布來闡述其抗截獲性能[3]；Fang X J將多參數加權類分數階傅里葉變換(multi-parameters weighted-type fractional Fourier transform,MP-WFRFT)性能與傳統方法進行比較時亦使用了基帶信號的星座圖[4]。綜上所述，目前對WFRFT抗截獲性能的研究僅停留在未加載波的基帶信號星座圖上，對加載波后的調制波形未進行研究，且當前研究中有關抗截獲性的證明停留在定性分析階段，并未提出實際的定量評價指標。

針對上述問題，本文提出一種應用在Ka波段衛星上的WFRFT抗截獲調制方案。對通信過程中基帶信號及調制信號波形特征展開研究,引入互相關系數概念， 研究WFRFT處理前后的調制信號波形的相關程度，建立抗截獲性能的具體評價指標。

1 正交相移鍵控—WFRFT抗截獲信號研究

1.1 正交相移鍵控信號基礎

正交相移鍵控(quadrature phase shift keying,QPSK)信號波形的調制過程為：首先,數據源在基帶上進行映射，將得到的結果分為實部與虛部兩部分，并分別作為同向/正交(in-phase/ quadrature,I/Q)2路的幅度信息；對2路信號加載波，合成最終的信號波形。QPSK映射關系如表1所示。

表1 QPSK映射關系

以1 kHz進行采樣的傳統QPSK調制波形序列s(n)的數學表達式為

s(n)=I(d(n))·cos(2πfcn)+Q(d(n))·

sin(2πfcn

(1)

式中 I(·)為取實部運算,Q(·)為取虛部運算,d(n)為按表1規律映射后得到的基帶信號,fc為載波頻率。

1.2 QPSK-WFRFT抗截獲信號研究

由表1可知，I，Q兩路信號中僅存1與-1共2種幅度，得到的最終信號波形具有較強的規律性，易被第三方截獲。為使信號具有抗截獲性，本文對傳統QPSK調制方式進行改進，在信號基帶部分加入WFRFT處理，新的調制過程如圖1所示。

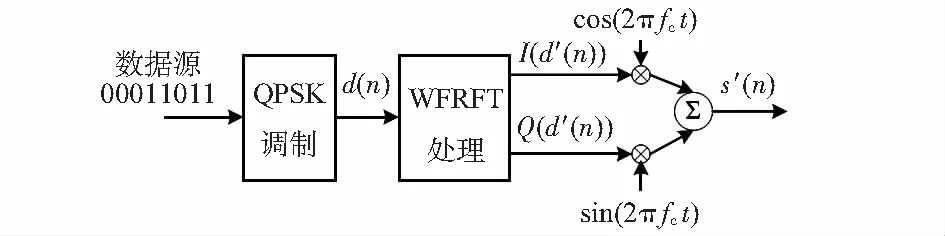
圖1 QPSK-WFRFT調制過程

其中，WFRFT處理模塊的結構如圖2，信號d(n)通過1次離散傅里葉變換(discrete Fourier transform,DFT)和 2次反轉后分別與加權系數wl(l=0,1,2,3)相乘，各項相加后得到最終信號輸出。

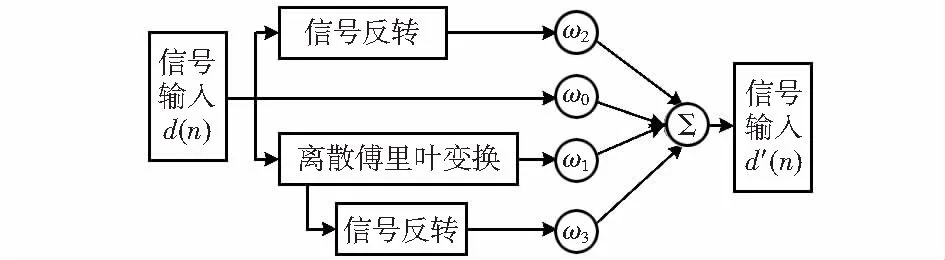
圖2 WFRFT處理模塊結構

離散WFRFT的數學表達式為[5]

d′(n)=w0(α,V)d(n)+w1(α,V)D(k)+

w2(α,V)d(-n)+w3(α,V)D(-k)

(2)

式中wl(α,V)(l=0,1,2,3)為WFRFT的變化階數；α為WFRFT的變換階數，可在[0,4]范圍內任意取值；V為尺度向量，取值為任意整數，由Mk=[m0,m1,m2,m3]與Nk=[n0,n1,n2,n3]組成;D(n)為d(n)的歸一化DFT，DFT變換對的表達形式為

(3)

wl(α,V)還可進一步表示為[6]

(4)

由式(2)、式(1)，得到QPSK-WFRFT調制信號為

s′(n)=I[w0(α,V)d(n)+w1(α,V)D(n)+

w2(α,V)d(-n)+w3(α,V)D(-n)]·cos(2πfcn)+

Q[w0(α,V)d(n)+w1(α,V)D(n)+w2(α,V)d(-n)+

w3(α,V)D(-n)]·sin(2πfcn)

(5)

式中 當加權系數wl(α,V)中α≠0時，基帶信號與調制波形受其影響會發生改變，改變的程度取決于參數α與V的取值，其中，α造成相位的旋轉與混淆，V對混淆程度存在微小的影響[7]。本文忽略V造成的影響，令V=0，則最終的波形序列為

s′(n)=I[w0(α)d(n)+w1(α)D(n)+w2(α)d(-n)+

w3(α)D(-n)]·cos(2πfct)+Q[w0(α)d(n)+w1(α)D(n)+w2(α)d(-n)+w3(α)D(-n)]·sin(2πfct)

(6)

2 QPSK-WFRFT抗截獲信號的波形

2.1 QPSK-WFRFT基帶信號

式(2)為QPSK-WFRFT基帶信號，式(6)為經變頻后的調制信號。兩者均受到變換階數α的影響，由于WFRFT信號特征具有對稱性[7]，故本文只研究α=[0,1]的情況，設數據源長度為10 000，當α取0，0.01，0.1，0.5，0.8，1時,分別對基帶信號與調制波形進行仿真。為方便觀察，截取前100個信號進行分析。發現α=0時，WFRFT未對信號處理，此時，相當于信號只進行了QPSK映射，基帶信號的同相分量與正交分量特征無變化。

當α為0.01，0.1時，經WFRFT處理的基帶信號，α取值較小時，WFRFT對基帶信號特征的改變不明顯，處理前后信號特征具有一定相似性，存在被第三方截獲的風險。

α分別取0.5，0.8，1時，隨著α取值增大，I/Q分量上產生的幅度值增多，變換前后的信號區別增大，第三方截獲通信內容的可能性較低。

2.2 QPSK-WFRFT抗截獲信號波形仿真

式(6)給出信號在信道中傳播的波形，本文以Ka波段衛星為研究對象，信號波特率取100 bps，載波頻率fc為23 GHz,分別對α為0，0.01，0.1，0.5，0.8，1的QPSK-WFRFT調制波形進行仿真，結果如圖3所示，可以看出α會對最終的發射波形造成影響，不同的α產生的調制波形不同，α值越大，產生的波形與原QPSK調制信號波形區別越明顯，第三方通將WFRFT處理前后波形聯系起來的可能性越低。

圖3 不同α時的QPSK-WFRFT波形

3 QPSK-WFRFT波形抗截獲性研究

3.1 QPSK-WFRFT與QPSK波形的互相關性分析

現有WFRFT研究中，主要通過基帶信號星座圖分布特征定性說明其抗截獲性，缺乏定量分析的理論指標。相關系數可以作為一種表征隨機變量或信號之間關聯程度強弱的統計指標[8～12]。

互相關系數的表達式為

(7)

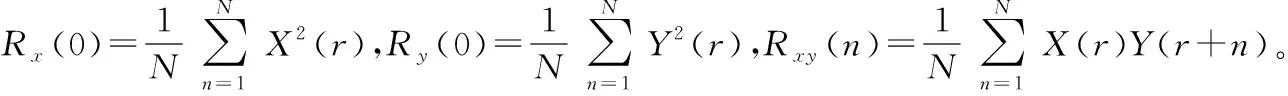
3.2 QPSK-WFRFT波形互相關系數仿真

對載波頻率為23 GHz，長度為10 000的QPSK-WFRFT調制信號波形仿真，變換階數α分別取0，0.01，0.1，0.5，0.8,1，求得到的新波形與QPSK調制信號的互相關系數,相關系數的仿真結果如圖4所示。

圖4 不同α時的QPSK-WFRFT波形互相關系數

對圖4進行分析：信號的隨機性使得僅在延時為0 s時出現相關峰，該現象表明信號不具有周期性；變換階數α增大的同時，相關峰數值逐漸減小；當α=0.5時，WFRFT處理前后信號波形的相關峰數值僅為0.247 0，統計學角度上講，兩者之間呈現弱正相關關系，即已無法通過常規手段建立兩者之間的聯系；而當α=0.8或1時，兩者相關峰的取值小于±0.1，幾乎不可能與原QPSK的信號波形建立聯系，故QPSK-WFRFT調制信號具有抗截獲性，且抗截獲性能隨α增大而增強。

表2給出了對不同參數之間的互相關系數，表中數據表明：對于原QPSK調制信號波形，QPSK-WFRFT采用不同變換階數α時得到的最大互相關系數不同，隨著α值增大，最大相關系數的值減小；兩個使用不同α值的QPSK-WFRFT調制信號波形，變換階數差值越大，相關性越弱，該結論表明，當第三方已知合法用戶使用QPSK-WFRFT進行信號調制，截獲信號所使用的α與合法用戶參數差值過大時，亦無法截獲信號。

4 合法用戶接收性能分析

對于合法用戶，通信質量需要得到保證。假設收發兩端完全同步、濾波器對信號的影響忽略不計，對不同變換階數α、不同信噪比(signal to noise ratio,SNR)條件下的比特誤碼率(bit error rate,BER)進行仿真分析，其中,α的范圍為[0,2]、SNR的范圍為[0,12]。

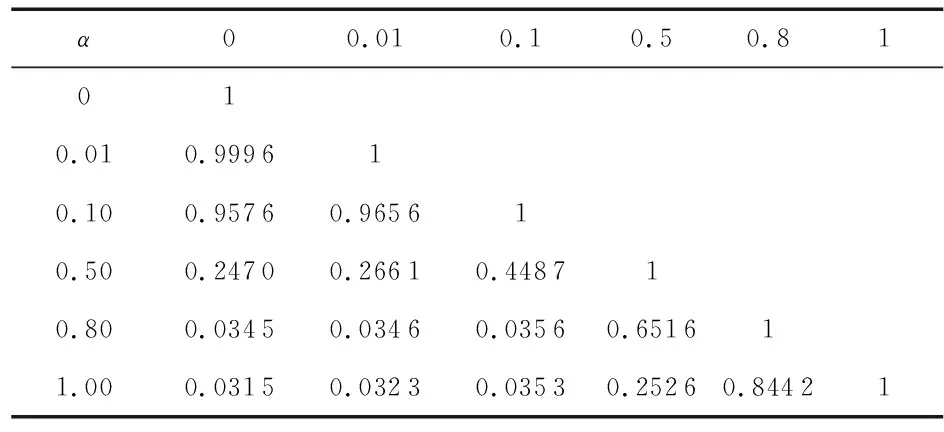
表2 不同變換階數產生波形的最大互相關系數

圖5反映了合法用戶α,SNR與BER之間的關系。圖中BER的變化趨勢表明：合法用戶使用不同的α對信號進行調制解調時，系統的BER未受到影響，BER主要受到SNR的影響,且SNR取6.8時，系統BER為1.107×10-2,該數值與QPSK調制信號的理論誤碼率數值相近，即新方案能夠保證通信的可靠性；故QPSK-WFRFT調制方式能夠應用在Ka波段衛星通信中。

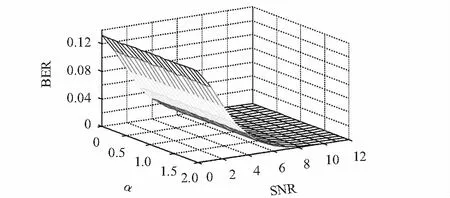
圖5 合法用戶接收BER，SNR與α的關系

5 結 論

提出將QPSK-WFRFT調制方案應用在Ka波段衛星通信系統當中，研究其基帶信號與調制信號波形特征，通過與原信號對比，得出其具有抗截獲性的定性結論；引入相關系數概念，通過WFRFT前后信號波形的相關系數定量分析新調制方案的抗截獲性能，得到α值越大，第三方截獲通信的可能性越小的結論；最后通過對合法用戶接的BER分析驗證了方案的可行性。

QPSK-WFRFT波形互相關系數仿真結果中，當α=0.8時，相關系數出現峰值為負的情況，對這種情況的理論分析將成為下一步研究的重點，該研究將有助于WFRFT最優化變換階數的選取。