基于歐氏距離與多種搜索策略的人工蜂群算法*
佘合一, 吳錫生
(江南大學 物聯網工程學院,江蘇 無錫 214122)
0 引 言
人工蜂群(artificial bee colony,ABC)算法[1]因結構簡單、控制參數較少、魯棒性強等特點,越來越多地被各界學者所關注與研究。但其在優化過程中,存在收斂精度低、收斂速度慢、易于早熟的缺點,其主要原因是ABC算法探索能力強而開發能力較弱[2]。
文獻[3]將混沌序列引入蜂群算法中,并用禁忌表記錄已搜索的局部最優點來達到控制性的搜索;文獻[4]中針對標準ABC算法中新個體的產生,運用了一種互學習策略,讓新個體的產生更傾向于在適應度更優的父代個體周圍;文獻[5]采用一種有方向的搜索策略,使搜索沿著最優個體的方向進行,減少了搜索過程中的盲目性。上述改進算法的性能都有了一定程度改善, 但仍缺少對算法的探索能力與開發能力的平衡。
為此,本文提出了一種基于歐氏距離與多種搜索策略的改進人工蜂群算法(improved ABC,IABC)。在IABC算法中,由三種具有不同特點的搜索策略組成策略池,用來實現更新的鄰居由指定半徑的歐氏距離決定。因每個搜索策略的特性不同,因而最大程度的平衡了算法的探索能力與開發能力。通過對標準測試函數的仿真實驗,并與標準ABC算法及相關改進算法進行比較, 表明了本文所提出的IABC算法的有效性,較好地提高了算法的收斂速度和收斂精度。
1 人工蜂群算法搜索策略
對于一個D維空間的搜索問題,種群規模為2×SN,蜂群覓食過程中的蜜源相當于D維空間域中的一個可行解,第i個蜜源位置xi={xi,1,xi,2,…,xi,D},每一個蜜源與雇傭蜂和跟隨蜂一一對應(雇傭蜂個數=跟隨蜂個數=SN),蜜源的優異程度則對應其解的可行度,即適應度。
ABC算法最初根據問題域按式(1)隨機產生一個初始種群
xij=xmin,j+rand(0,1)(xmax,j-xmin,j)
(1)
式中i=1,2,…,SN,j=1,2,…,D,xmin,j和xmax,j分別為變量xij的下界和上界。
初始化之后,雇傭蜂根據蜜源進行開采,在蜜源的周圍由式(2)進行隨機搜索
vij=xij+φij(xij-xkj)
(2)
式中k為隨機產生的整數,k=1,2,…,SN且k≠i,j=1,2,…,D;φij∈[-1,1]為一個隨機數。
2 本文IABC算法
2.1 3種搜索策略
不同的搜索策略需具有不同的搜索特性,滿足不同特性的優化問題,使搜索的不同階段都能有合適的搜索策略。在文獻[2]提出了全局最優指導的蜂群算法(global ABC,GABC),利用最優蜜源來指導候選蜜源的搜索。GABC的搜索策略公式如下
vij=xij+φij(xij-xkj)+ψij(gbestj-xij)
(3)
式中gbestj為全局最優解的第j維值,k=1,2,…,SN,且k≠i,j=1,2,…,D,φij∈[-1,1],ψij∈[0,C],當C=1.5時效果最好。
文獻[6]提出了一種改進的ABC算法(modified ABC,MABC), MABC的搜索策略公式為
vij=xb,j+φij(xr1,j-xr2,j)
(4)
式中xb,j為全局最優解的第j維值,r1=1,2,…,SN,r2=1,2,…,SN且r1≠r2≠i,j=1,2,…,D。
GABC算法參考文獻[7]進一步對式(4)修改為
vij=xb,j+φij(xb,j-xkj)
(5)
由式(3)、式(5)以及式(2)組成了搜索策略池。在跟隨蜂開發蜜源階段,利用策略池中3種搜索策略分別產生3個候選蜜源,由產生的候選蜜源計算對應的適應度,根據3個候選解的適應度進行擇優選取。由策略池中3種不同特性的搜索策略可以在算法搜索階段表現出不同的搜索特點,使算法在不同搜索階段都有適合的搜索策略。
2.2 歐氏距離在搜索策略中的應用
在式(3)、式(5)中忽略了解結構相似性的聯系,破壞解的多樣性。考慮到解結構之間的相似性,可以采用歐氏距離來劃分解的鄰域[8],鄰居的解結構存在較高的相似度。
如二個蜜源xi與xm之間的歐氏距離用d(i,m)表示,那么對于xi與所有蜜源的平均距離可表示如下
(6)
如果d(i,m)≤r×mdi,則xm是xi的一個鄰居,參數r為鄰域半徑。
蜜源xi獲得其全部鄰居蜜源后,根據每個鄰居蜜源適應度選出鄰居內最優蜜源xb,其計算公式如下
(7)

2.3 IABC算法流程
1)設置算法參數,最大循環次數FES,控制參數limit,隨機產生初始解集,i=1,2,…,SN,j=1,2,…,D,計算解的適應度。
2)雇傭蜂按式(2)搜索候選蜜源vi,計算其適應度,并進行貪婪選擇,若vi適應度仍小于原先蜜源,則limit+1。
3)跟隨蜂根據輪盤賭方式對蜜源進行概率性選擇,對選擇的蜜源計算與其他蜜源歐氏距離,根據式(6)計算出平均距離mdi,確定其鄰居蜜源。
5)分別用式(2)與步驟(4)更新的式 (3)、式(5),產生3個候選蜜源,計算3個蜜源的適應度,并根據3個候選蜜源的適應度進行貪婪選擇,生成vi。
6)對生成的vi與原先蜜源進行貪婪選擇,若vi的適應度仍小于原先蜜源,則limit+3。
7)判斷是否有需要被放棄的蜜源,若有, 則重新產生新的蜜源。
8)如果滿足終止條件, 則算法結束, 輸出最終結果; 否則,轉步驟(2)。
3 實驗與結果分析
3.1 測試函數選擇
本文選取了6個典型的測試函數進行測試。其中,f1,f2,f3(Sphere,Rosenbrock,Schwefel)為單峰函數,在定義域范圍內只有1個極值,用于測試算法的收斂精度與收斂速度;f4,f5,f6(Rastrigin,Griewank,Ackley)為多峰函數,在定義域范圍內存在多個極值,用于測試算法避免早熟能力與全局尋優能力。其中,f2全局極小值位于一條平滑而狹長的拋物線形狀的山谷底部,該函數中變量之間具有很強的關聯性,不易找到其全局極小值,通常用該函數來評價優化算法的性能。
3.2 結果分析
在對本文算法(IABC),ABC算法,文獻[5] (directed ABC,dABC)算法和文獻[9](quick ABC,qABC)算法進行對比實驗時,實驗參數設置為:種群規模為50(SN=25),函數維度D=30,limit=300,最大循環次數FES=1 000,鄰域半徑r=1.5。將4種算法對每個測試函數獨立運行30次,測試結果如表1所示。

表1 4種算法性能比較
從表1可以看出:在所有的測試函數中標準的ABC算法的平均值最高,除了函數f2的方差要低于dABC算法與qABC算法,其他函數的方差均高于其他3個算法,說明標準ABC算法解的精度與穩定性較差;dABC算法與qABC算法相對于標準的ABC算法,無論在單峰函數還是在多峰函數中,最優值、最差值與平均值3個方面的實驗數據均明顯好于標準ABC算法,其中,qABC算法在函數f4中得到了函數的理論最優值,只有在函數f2中的方差要比標準ABC算法大,可知dABC算法與qABC算法解的精度較好。在穩定性方面,總體上較標準ABC算法要好。
本文IABC算法在6個函數中,其性能都優勢明顯。為了更直觀地顯示本文IABC算法的收斂速度與收斂精度,圖1~圖6為4種算法對測試函數的收斂曲線。結合表1與圖1~圖6,可以發現,本文算法在每一個測試函數中,每項數據都明顯優于另外3種算法。在所有測試函數中,本文IABC算法的最優值、最差值與平均值與方差都優于其他算法。對于解的精度:在測試函數f2中,標準ABC算法、dABC算法與qABC算法很容易陷入局部最優解,很容易早熟收斂,而本文IABC算法的解明顯好于另外3個算法的解,并且仍然有向最優解進化趨勢。根據圖4和圖5可以看到本文IABC算法對測試函數f4與f5分別迭代500多次與600多次便找到了理論最優值。對于收斂速度:從圖1~圖6可以直觀的看出,標準ABC算法收斂速度緩慢,dABC算法與qABC算法相對標準ABC來說,收斂速度得到改善,但改善的幅度仍然不是很大,而本文IABC算法的收斂速度相比較另外3個算法的收斂速度都有了很大改善。

圖1 Sphere函數進化曲線
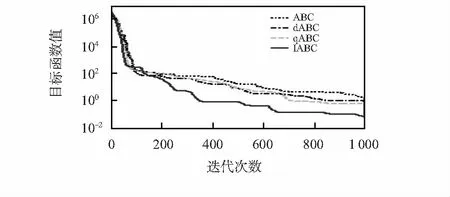
圖2 Rosenbrock函數進化曲線

圖3 Schwefel函數進化曲線

圖4 Rastrigin函數進化曲線

圖5 Griewank函數進化曲線
本文IABC算法與qABC算法都引入了歐氏距離,來確定具有相似解結構的最優鄰居,以避免利用全局最優解而忽略其他較優解的開發能力。但本文IABC算法在歐氏距離的基礎上,用3種不同的搜索策略,來滿足不同搜索階段的特性,使搜索過程中每個階段都有適合的搜索策略,以此均衡算法的探索能力與開發能力,增加解的多樣性,使算法更容易找出最優值,從而進一步提高了收斂速度與精度。

圖6 Ackley函數進化曲線
4 結 論
提出了一種改進的基于歐氏距離與多種搜索策略的人工蜂群算法(IABC)。仿真結果表明:本文算法在求解函數最小值優化問題時,能夠顯著提高收斂速度,并能有效地避免算法陷入局部最優,提升解的收斂精度。該算法可以很好地解決復雜優化問題,可以將本文IABC算法應用到圖像處理中。如何利用IABC算法進行圖像分割中最優閾值的選取是下一步的研究內容。

