基于改進ICP算法的點云拼接方法*
楊 杰, 盧鈺仁, 田 穎, 呂曉玲
(河北工業大學 機械工程學院,天津 300130)
0 引 言
點云數據的拼接配準是物體三維重建過程中最重要的環節,直接影響處理后的整體精度[1]。目前的點云拼接大多是兩兩拼接配準問題,最初采用的方法是順序拼接[2],其核心思想是兩兩拼接,該方法簡單直接,但評估點云之間的包含關系[3]和重復拼接的累積誤差,會嚴重影響整體拼接的精度。對此,Nishino K[4]根據各個點云之間的對應關系提出了一種多視角拼接算法,但大型場景中多視角的點云數據龐大,計算點云之間的收斂十分緩慢,降低了局部點云拼接的準確性和效率。近年來,研究由局部拼接轉向全局拼接。利用平差方法[5]估計全局最優坐標轉換參數提高配準精度與可靠性是一種最常用的方法。
本文根據拼接中大角度變換存在的問題,提出了一種提取拼接點對的條件約束方法,在對點云數據進行粗拼接時,選取預參考點并對兩組點云中對應點關系進行改進,對獲取的不同幀數的點云數據進行約束條件的比較,去掉不符合條件的點云數據后,再對粗拼接數據進行精確拼接。針對本文提出的算法對室內室外場景進行實驗,以驗證所提出的方法的可行性。
1 點云數據粗拼接
1.1 拼接策略選取
三維幾何模型的變換通常包括旋轉、平移和縮放,在拼接過程中不考慮縮放,只需要求得目標點云集B到源點集A的旋轉矩陣R和平移向量T,使得經過左邊變換后得到的旋轉矩陣(R·A+T)與目標點云集B之間的距離最小。
經典迭代最近點(iterative closest point,ICP)算法中使用的點與點的對應關系為
d=min‖X-(R·A+T)2‖
(1)
因此,經典ICP算法[6]需要對點云遍歷處理,由于點云數據中法向量[7]是點云的重要參數,在拼接過程中也需要對其進行計算,所以將對應點對的關系改進為法向量之間的對應關系,即點與面的對應關系,如圖1所示。
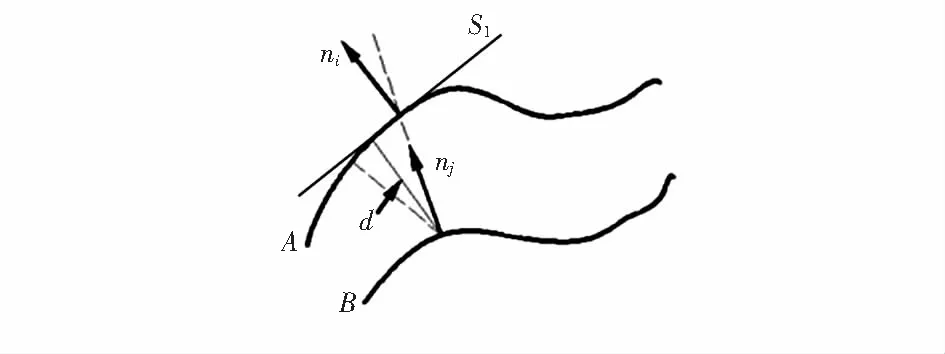
圖1 點到平面距離示意
d′=min‖[X-(R·A+T)2]·ni‖
(2)
式中ni為待拼接數據點的法向量。
1.2 預參考點對選取
本文采用了對點云數據中點與其鄰域點之間的法向量夾角的變化程度來評估點對之間的關系。如圖2所示,若夾角變化程度大,說明該模型曲面變化復雜;若夾角變化程度小,說明模型曲面平滑。選取出點云模型中法向量變化突出的點,精簡對應點對。因此,設定點云模型中某一點Pi處的法向量變化趨勢即其特征變化程度為其法向量與其近鄰點法向夾角的算術平均值
(3)
式中θij為點Pi的法向量與其近鄰點Pj的法向量的夾角,n為比例系數。
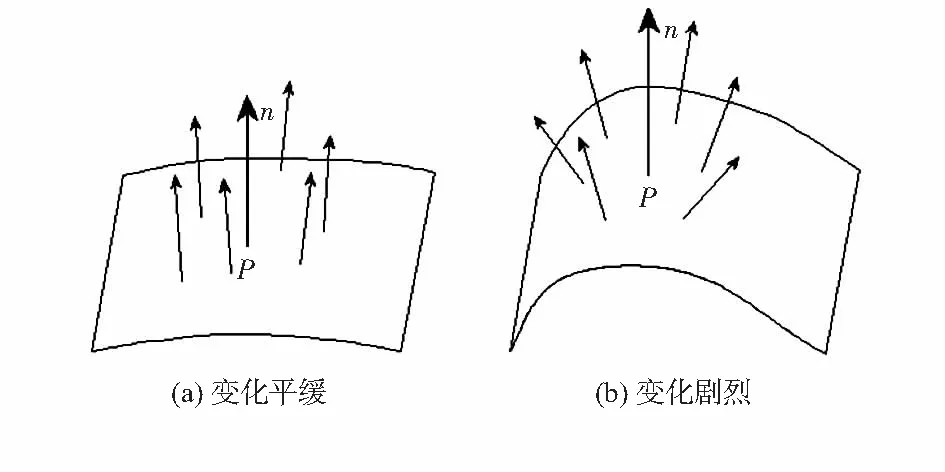
圖2 不同區域的方向量示意
根據點云數據模型體積V和點數量的大小n決定取不同的σ值進行分析,如圖3所示,σ取值較小時,將會對原點云模型的細節信息保存得相對完整,但局部信息去除較多;σ取值較大時,參考點集的點密度相對較大,計算保留的點較多。σ一般取5~10之間。

圖3 不同σ值所對應的參考點集
獲取參考點對后即可對點云數據進行拼接處理,對點云模型的粗拼接效果如圖4所示,經過點云粗拼接后的兩幅點云數據已經重合了很大部分。

圖4 點云粗拼接效果
2 精確拼接點對獲取
本文用曲率表示關鍵點的局部近鄰域形狀變化趨勢,并將其作為識別點云模型特征的重要依據。
設曲面S:r=r×(u:v)在點的主方向為(d)=du:dv,若定義Kn為A點處的主曲率,則Kn一定滿足[11]
(L-KnE)(N-KnG)-(M-KnF)(M-KnF)=0
(4)
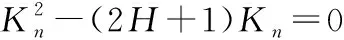
對選取的對應點對進行曲率計算,因為在計算機測量和計算時會出現不可避免的偏差,建立以下約束條件
(5)
如果點云中的Bi點不滿足式(5),需要將所選點剔除,選取另外互不共線的點對繼續進行比較,直至搜索完全參考點對點,找到點Ai所有可能匹配點Bi。
3 建立約束條件
1)對應點之間距離約束
若兩組模型的拼接點對是正確拼接匹配點對,根據剛體不變性及實際應用情況,只需滿足:|dist(xi,yi)|≈|dist(xj,yj)|。計算每個初始點對
(6)
式中δ1為設定的距離誤差,若計算兩點間距離滿足式(6),則將點對(xj,yj)記為相對于點對(xi,yi)的符合距離約束的點對。
2)對應點的曲率約束
根據關鍵點的曲率值建立如下約束條件
(7)
式中δ2為給定的曲率誤差。
4 點云數據精確拼接
將粗拼接后的結果作為新的初始位置,利用改進ICP算法進行精確拼接。雖然只是經過了粗拼接后,但已經得到了較好的初始位置關系,計算出的旋轉矩陣R和平移矩陣T誤差最小,可以得到最優變換矩陣
(8)

由于對選取點對和計算點的距離上有優化,并且對精確點對有優化和約束,所以,如表1所示,算法在點云拼接速度和精度上有所提高。

表1 不同點云拼接算法結果比較
點云精確拼接處理效果如圖5所示,在粗拼接的基礎上對點云數據進行精確拼接并進行點云融合。可以看出:兩幅大角度的點云圖像經過點云精確拼接后能完整地重現真實物體的特征。

圖5 點云精確拼接示意
5 結 論
本文針對點云數據獲取時,角度差異較大的數據拼接誤差較大的問題,分析了兩幅點云之間點與點之間的關系,提出了點到面的計算方法,并根據點的法向量的變化提取預參考點,簡化了兩組點云之間的計算復雜程度。對拼接點云進行優化約束,求得精確點對完成點云拼接。實驗結果表明:與傳統的點云拼接算法比較,本文改進的算法能夠有效提升處理速度并減少了實驗誤差,拼接算法融合后的點云數據能夠很好地達到重建的精度要求。

