非線性多智能體系統的分布式編隊控制

連文瑜 ，劉 佳 ，張運喜 ，李偉勛

（1.天津職業技術師范大學天津市信息傳感與智能控制重點實驗室，天津 300222；2.天津職業技術師范大學自動化與電氣工程學院，天津 300222；3.天津職業技術師范大學理學院，天津 300222）

隨著科學技術的發展和通訊技術的應用，多智能體系統的一致性在許多研究領域受到廣泛關注，如編隊控制、分布式計算和機器人系統等[1-3]。多智能系統是多個智能體的組合，它們通過相互間的合作協商來完成單個智能體不能完成的任務，多智能體系統的一致性即設計適合的控制協議使各個智能體達到相同的狀態。多智能體系統的編隊控制與一致性問題有著密切關系，在編隊控制時，智能體之間不僅要滿足某些狀態量使之達到一致，還需要和原來預先給定的隊形保持一致。有許多學者對多智能體系的編隊控制問題進行了研究，研究方法主要有基于領導-跟隨的方法[4]，基于行為的方法[5]，基于虛擬結構式的方法[6]。文獻[7]針對一階多智能體系統，基于一致性方法來研究多智能體系統分布式編隊控制。文獻[8]針對一階系統設計控制協議，研究了離散多智能體系統在固定有向拓撲結構中的分布式編隊控制。在考慮二階多智能體系統時，與一階多智能體系統有所不同，單個智能體的動力學模型不僅與位置有關，還與速度有關。文獻[9]研究二階動力系統的一致性問題，提出簡單的二階一致性協議，實現了多智能體系統的編隊控制。文獻[10]實現了二階多智能體系統的環形編隊控制研究。文獻[11]研究了多智能體的自適應算法。但在實際的應用過程中，多智能體系統具有非線性動力學特性[12-13]，因此，研究非線性多智能體系統的編隊控制十分必要。文獻[14]對含有非線性特性的二階多智能體系統，給出了一致性控制的研究。本文基于一致性協議，研究二階多智能體系統的編隊控制問題。

1 分析工具

1.1 圖論知識

代數圖論為重要的研究工具，將多智能體系統中的每個智能體看作一個質點，它們之間的關系可以用圖論的方式描述。

令 G（Q，E，A）為有向圖，其中 Q={q1，q2，…，qn}表示n個節點的集合，E∈Q×Q表示有向邊的集合，A表示鄰接矩陣。記eij=（qi，qj）∈E為有向邊，qi為邊的父節點，qj為邊的子節點，邊的方向為由qi到qj。通常用鄰接矩陣來描述各節點之間的關系，鄰接矩陣為：

式中：如果第j個節點能接收到來自第i個節點的相關信息，則aij＞0，?i≠j。aij為邊（qi，qj）的權值。否則，aij=0，而對角線上的元素aii=0，則說明該有向圖中不含有閉自環。在圖中，節點qi的入度用degin（qi）表示，出度用degout（qi）表示。

圖的Laplacian矩陣用另外一種方式描述了所對應的圖的所有信息，定義如下：

式中：D為圖G的入度矩陣，D=diag（degin（q1），degin（q2），degin（qn））；A為鄰接矩陣。

1.2 相關數學工具

矩陣的Kronecker積是一種重要的矩陣乘積，在矩陣理論的研究中具有廣泛應用，同時也是在研究控制系統理論時的重要數學工具。

定義 1[15]設 A=[aij]∈Rm×n，B=[bij]∈Rp×q，則分塊矩陣

稱為矩陣A與矩陣B的Kronecker積，記為A?B。

下面介紹本文用到的相關引理：

引理1[16]（Schur補引理）給定的對稱矩陣S=以下2個條件為等價的：

引理2[17]對于任意的常向量a，b∈Rn和正定矩陣Φ∈Rn×n，以下不等式成立：

2 問題描述與分析

2.1 系統描述

本文所研究的多智能體系統是由1個領導者和n個跟隨者組成的。領導者用0來標記，跟隨者用1，2，…，n來標記。

假設所考慮的跟隨者智能體的動態模型為：

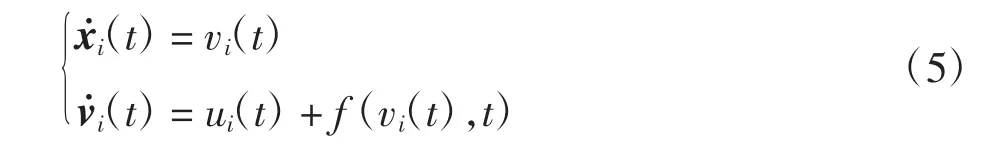
式中：xi（t）∈Rm為第i個智能體的位置向量；vi（t）∈Rm為速度向量；ui（t）∈Rm為控制輸入；f：Rm×R→Rm為連續可微的函數向量。

領導者智能體的動態模型為：

式中：x0（t）∈Rm為領導者的位置向量；v0（t）∈Rm為速度向量。

假設1非線性動態f（vi（t），t）（i∈{0，1，2，…，n}）是連續可微的函數向量，存在非負常數ρ，對于任意的t≥0滿足下列條件：

定義2為多智能體系統領導-跟隨編隊控制問題可解的定義。

定義2考慮所給出的多智能體系統，在任意的初始狀態xi（0），vi（0）下，領導者和跟隨者的位置和速度應該滿足下列要求：

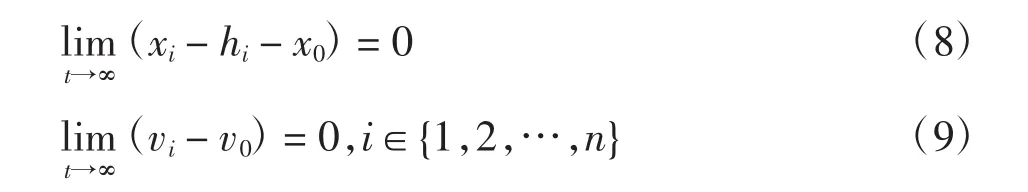
式中：hi∈Rm為第i個智能體與領導者之間期望的隊形常向量。

根據所給出的多智能體系統，控制器設計如下：

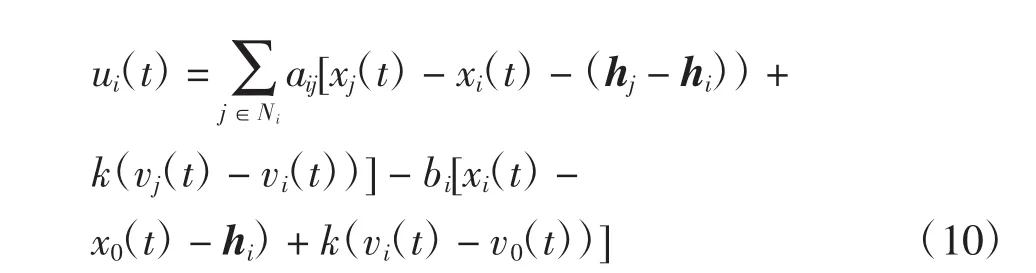
式中：Ni為第i個智能體在圖G中的鄰居集合；k＞0為速度增益；hi為第i個智能體與領導者之間期望的隊形向量；hj為第j個智能體與領導者之間期望的隊形向量；aij＞0為第i個智能體與第j個智能體的連接權值；bi為第i個智能體與領導者之間的連接權值，分別定義為：

將式（10）代入系統（5）中，得：

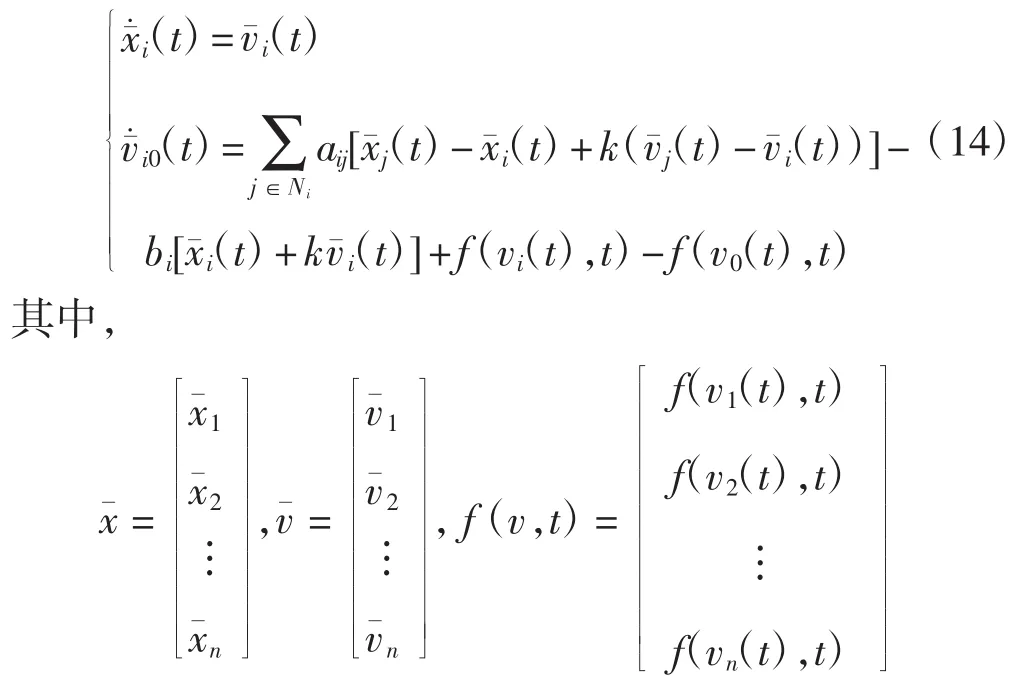
通過Kronecker積，可以把誤差系統（14）轉化為矩陣形式：

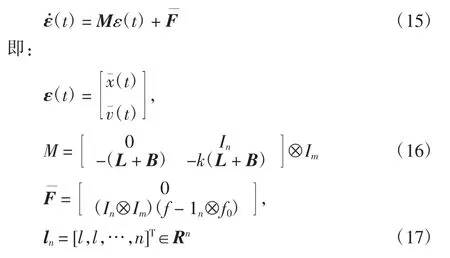
式中：L為圖G的Laplacian矩陣；B為跟隨者與領導者之間的連接矩陣，記作 L=diag（b1，b2，…，bn）。

2.2 主要結果

定理1針對具有非線性特性的多智能體系統，對于給定的正常數ρ，存在適當維數的正定矩陣P，R滿足下列的線性矩陣不等式：

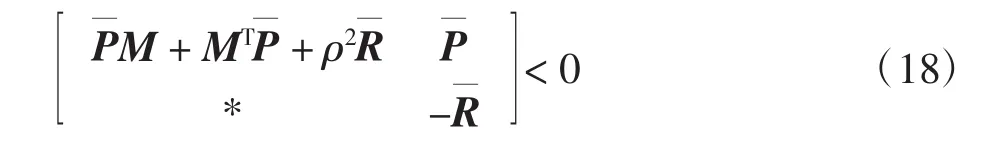
證明選取Lyapunov函數

對 V（t）沿著系統（15）求導，可得：

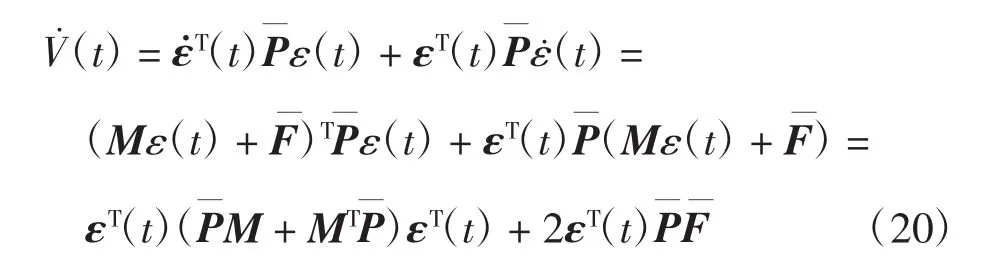
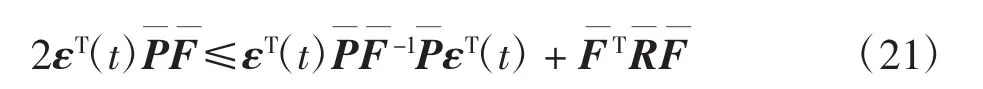
將式（21）代入式（20）中，可以得到：

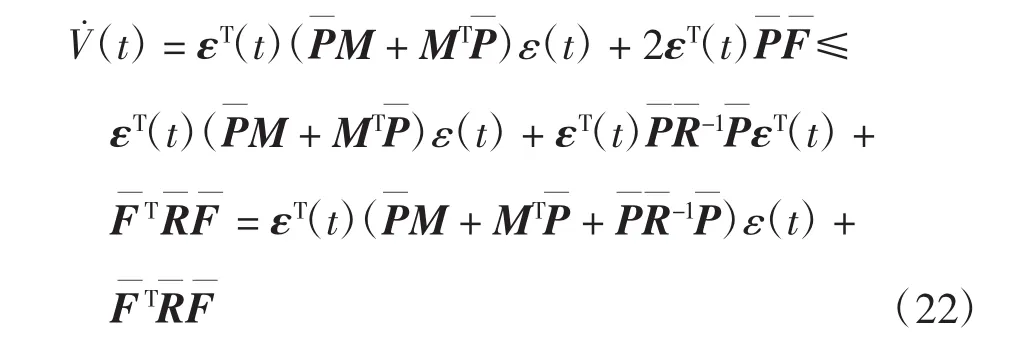
又由假設1可以得到：

將式（23）代入式（22），可以得到：

3 數值仿真

3.1 仿真例子

例1考慮該多智能體系統由4個跟隨者與1個領導者智能體所組成，智能體之間的拓撲結構關系如圖1所示。

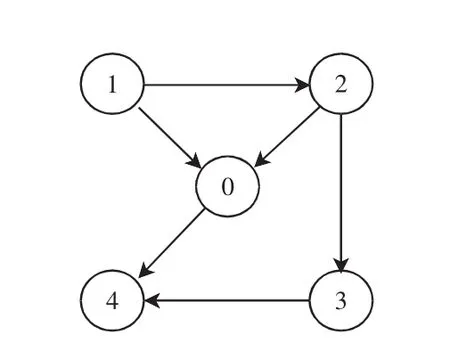
圖1 智能體拓撲結構

假設智能體之間的連接權值為0或1，則跟隨者之間所對應的Laplacian矩陣為：

跟隨者與領導者之間的連接矩陣為：

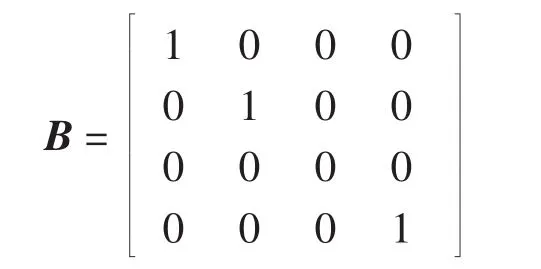
假設多智能體系統是在二維平面上的系統，且非線性動態為：

由假設1可得ρ=0.2，期望的隊形向量分別為：

令k=2，通過Matlab中的LMI工具箱，可以求解定理1中的線性矩陣不等式（18），求得可行解為：

3.2 仿真結果

通過仿真圖來描述多智能體的狀態軌跡及位置誤差和速度誤差的變化趨勢，智能體的狀態軌跡如圖2所示，位置誤差狀態軌跡如圖3所示，智能位置誤差狀態軌跡如圖4所示，速度誤差狀態軌跡如圖5所示，智能體的速度誤差狀態軌跡如圖6所示。

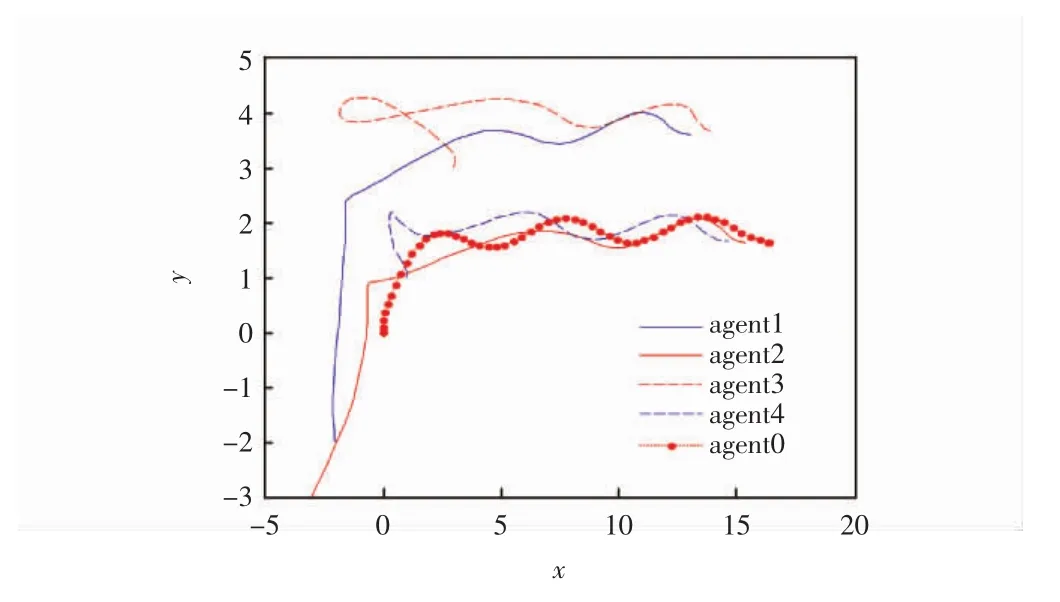
圖2 智能體的狀態軌跡

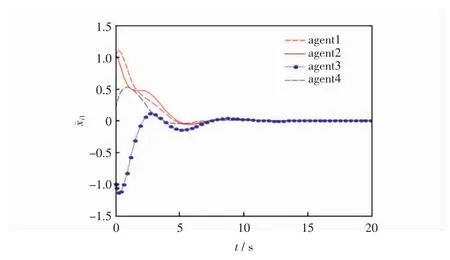
圖3 智能體的位置誤差i1狀態軌跡

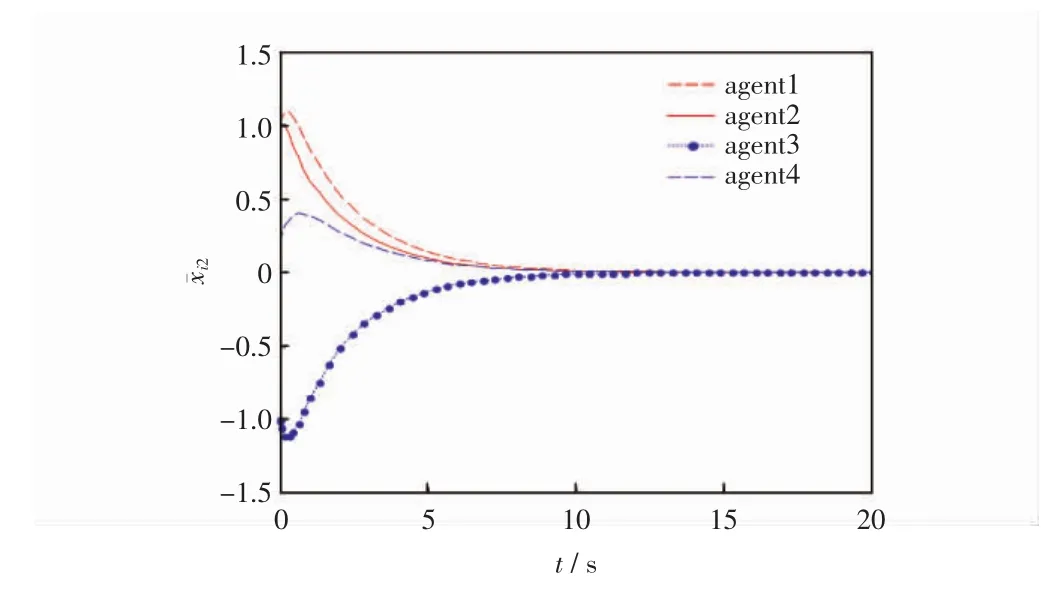
圖4 智能體的位置誤差ˉi2狀態軌跡

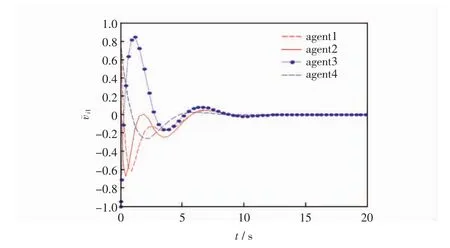
圖5 智能體的速度誤差ˉi1狀態軌跡

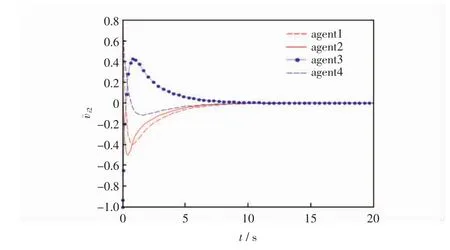
圖6 智能體的速度誤差ˉi2狀態軌跡

從圖2中觀察4個智能體與領導者的運動軌跡，可以發現智能體能夠達到所期望的隊形；從圖3和圖4這兩個圖中可以看出在二維平面下，多智能體系統的位置誤差在隨著時間的變化最終都會趨近于零，即跟隨者與領導者的位置可以達到一致；從圖5和圖6可以看出在經過一段時間后，多智能體系統的速度誤差會趨于零，即跟隨者的速度可以滿足領導者的速度，多智能體系統達到穩定的狀態，也就是說多智能體系統既能夠滿足期望的隊形，跟隨者又能夠與領導者的速度達到一致。因此，證明了所得理論的有效性。

4 結語

本文研究了二階多智能體系統的編隊控制，在具有非線性動態特性的情況下，設計了合適的分布式編隊控制協議，利用Lyapunov穩定性理論和基于線性矩陣不等式的方法對控制協議進行穩定性分析，得出多智能體系統能夠按照所期望的隊形運動，而且位置誤差和速度誤差在經過一段時間后趨于零，達到穩定狀態，通過數值仿真實例驗證了所得結論的有效性，即多智能體系統不僅能夠得到所期望的隊形，而且跟隨者的速度和領導者智能體的速度能夠達到一致。