MATLAB在高等數學信息化課堂教學中的應用

梁佩佩　王彩鳳　顧志琴

[摘要]高等數學是高職院校理工類專業學生必修的一門重要公共基礎課程，該課程的特點是具有高度的抽象性和概括性。如何把高等數學中抽象的概念和性質具體化，是一個值得長期研究的問題。在總結傳統課堂教學模式的局限性和了解MATLAB數據分析及可視化技術的基礎上，構建信息化課堂教學模式。在課堂教學過程中充分利用MATLAB軟件在繪圖和數值計算上的優勢，以高等數學中求解閉區間上連續函數的最大值與最小值為例，闡明MATLAB在高等數學信息化課堂教學中的應用。

[關鍵詞]高等數學;MATLAB;函數最值;應用

[中圖分類號]G712??????????? ?? ??????? [文獻標志碼]? A???????? ????????????? [文章編號]? 2096-0603（2018）36-0094-02

一、引言

高等數學是高職院校理工類專業學生必修的一門重要公共基礎課程，該課程在先修課程—初等數學的基礎上進行講授。高等數學課程理論嚴密，觀點抽象，內容多且復雜。掌握好該課程的基本內容不僅為學生后續專業課程的學習奠定必要的數學基礎，而且通過高等數學的學習有助于提高學生的邏輯思維能力、運算能力、抽象分析能力以及推理能力。

隨著計算機應用的快速發展，在高等數學教學過程中引入計算機軟件輔助教學是教學改革的一個部分。MATLAB是美國MathWorks公司出品的商業數學軟件，全稱為“矩陣實驗室”。常用于算法開發、數值分析、數據可視化以及數值計算的高級技術計算語言和交互式環境，應用領域極其廣泛。圖形用戶界面（Graphical User Interface）簡稱GUI，又稱圖形用戶接口，是指采用圖形方式顯示的計算機操作用戶界面。提供GUI的應用程序能夠使學生的學習和使用變得方便和容易;學生不需要知道應用程序究竟是怎樣執行各種命令的，只需要了解界面組件的使用方法，通過與界面交互就可以使指定的行為正確執行。

為了促進信息技術在高等職業教育教學中的廣泛應用，提高教學效果和教學質量，培養學生的自主學習能力，增強學生主動求知的欲望，本文以高等職業教育新形態一體化教材《高等數學》中第三章第四節“函數的最大值與最小值”為例，在MATLAB環境下，自主開發求解閉區間上連續函數最值的程序，讓學生更加直觀地理解閉區間上連續函數最值的求解過程。

二、傳統課堂教學模式

傳統高等數學課堂教學模式主要以教師講授為主，學生只是被動地接受信息。教師往往都是“一本書、一塊黑板、一支粉筆”貫穿整個課堂。課堂教學模式單一、死板，教師只重視知識的傳授和教學任務的完成，而忽視了對學生主觀能動性的培養。導致學生對知識的理解產生很大困難，從而影響學生對高等數學課程的學習興趣，同時也會禁錮學生的思維拓展和創新意識。為了適應當今科學發展的需要和高職院校的培養目標，培養高素質、高層次的應用型人才，教師應在教學過程中結合所學的高等數學內容，從實際出發，逐步激發學生對高等數學的學習興趣，從而讓其自主探索、研究。

另外，傳統高等數學課堂教學模式主要以課本的數學知識為基礎，概念、公式為主。高等數學的特點具有高度的抽象性與概括性，而且具有極強的嚴密性、精確性與邏輯性。高等數學教學的目的不僅是為學生提供一種計算的工具及計算的方法，更重要的是為學生提供一種抽象思維和邏輯思維的方法，使學生從有限的形象思維過渡到無限的抽象思維。通過學習高等數學，使學生學會分析與歸納的方法和技巧，提高學生邏輯推理與論證的能力，培養學生的數學素質，為進一步分析問題和解決問題奠定數學理論基礎。教師在教學過程中一再強調高等數學課程的重要性，但是由于高等數學的抽象性和嚴謹性，使大部分學生望而生畏。學生認為高等數學太抽象、枯燥，致使學習興趣每況愈下，不及格率大大增加。所以，有必要對高等數學的教學模式進行改革。

三、信息化課堂教學模式

在教育改革不斷深入的過程中，高等職業教育事業也發生了較大改變。現如今，教育事業是以教育信息化提高高等職業教育的教學質量和效率，這也是現代化教育中較為重要的一項工作。高等數學本身就是一門邏輯性較強且較為抽象的公共基礎課程，而以信息技術作為依托構建高等數學信息化課堂教學模式，則能在一定程度上起到較為良好的促進作用。為此，近年來我國高等數學課堂教學模式一直在積極圍繞信息技術手段進行相關研究，希望能夠以此推進高等職業教育質量工程，真正將高等數學教育和信息技術有效融合在一起。

信息化課堂教學模式是針對高等數學高度的抽象性和概括性這一特點，以現代教育教學理念為指導，以信息技術為支持，充分應用現代教育技術手段的課堂教學模式。信息化課堂教學模式突破了傳統教育時空、方式等方面的局限，彌補了傳統課堂教學模式的不足，調動了盡可能多的教學媒體和信息資源。并且在教師的組織和指導下構建一個良好的學習環境，充分發揮學生的主動性、積極性和創造性，以達到良好的教學效果。

本文在總結當前閉區間上連續函數最值教學中存在的問題和了解MATLAB數據分析及可視化技術的基礎上構建信息化課堂教學模式。其中，信息化教學手段之一是在MATLAB R2014b環境下編制“閉區間上連續函數最值的求解”程序，其初始界面如圖1所示。功能按鍵有顯示圖像和求最值;功能輸入鍵有輸入公式和輸入區間（左閉區間、右閉區間）等內容的輸入;功能輸出鍵有最大值和最小值。

首先學生按要求在輸入公式框輸入f（x）=2x3+3x2-12x+4，如圖2所示;然后在區間輸入框分別輸入-3和4，如圖3所示。

強大的繪圖功能是MATLAB軟件的特點之一。數據可視化的目的在于，通過圖形，從一堆雜亂的離散數據中觀察數據間的內在關系，感受由圖形所傳遞的內在本質。借助于圖像研究函數的性質是一種常用的方法。函數圖像的幾何特征與數量特征緊密結合，“以形助數”體現數形結合的特征與方法，培養學生數形結合的思想。數形結合就是將抽象數學語言與直觀圖形結合起來，使抽象思維與形象思維結合起來，通過“數”與“形”之間的對應和轉換解決數學問題。

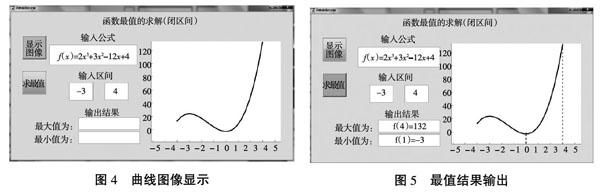
點擊“顯示圖像”，經過后臺自動運行程序，顯示該函數在[-3，4]區間的曲線圖形，如圖4所示。

點擊“求最值”，后臺按照首先求函數f（x）的導數f ′（x），其次令f（x）=0求得函數f（x）在（-3，4）內的所有駐點，并找出函數f（x）在（-3，4）內的導數不存在的點，然后比較函數在駐點和導數不存在的點處的函數值與函數在區間端點處的函數值f（-3）、f（4）的大小，其中最大者就是f（x）在[-3，4]上的最大值，最小者就是f（x）在[-3，4]上的最小值，如圖5所示。

四、信息化課堂教學模式的課堂調控

課堂時間為90分鐘，主要包括情景引入、最值求解、最值應用、課堂測試和評價體系五個環節，如圖6所示。其中，函數最值的求解程序貫穿于“最值求解”和“最值應用”兩個環節，其時間分別為25分鐘和35分鐘。

五、結論

利用日臻成熟的MATLAB數值分析及數據可視化技術打破傳統高等數學課堂教學模式，在MATLAB環境下自主開發求解函數最值的程序，讓學生更加直觀地理解函數最值的求解過程，讓學生從一堆雜亂的離散數據中觀察數據間的內在關系，感受由圖形所傳遞的內在本質，從而培養學生數形結合的思想以及提高教學效率和教學質量，最終達到培養學生的自主學習能力和增強學生主動求知欲望的目的。

參考文獻：

[1]張巖，吳水根.MATLAB優化算法[M].北京：清華大學出版社，2017.

[2]李娜，仁慶道爾吉.MATLAB在高等數學教學中的應用研究[J].大學教育，2012，1（11）：66-67，74.

[3]童德茂.探討Matlab在高職高等數學教學中的應用[J].阜陽師范學院學報（自然科學版），2010，27（1）：79-82.

[4]雍進軍.《高等數學》教學中應用MATLAB的探討[J].四川職業技術學院學報，2012，22（4）：84-86.

[5]司鳳娟.MATLAB軟件在高等數學教學中的應用[J].電子技術，2013，42（10）：39-42.