紅黑樹在含風電電力系統可靠性評估中的應用

栗 然， 童煜棟

(新能源電力系統國家重點實驗室(華北電力大學)，河北 保定 071003)

0 引言

隨著風電機組單機容量和風電場規模的不斷增大，迫切需要研究大型風電場并網對發輸電系統的影響及其帶來的風險，全面評估風電的價值[1]。風險與可靠性描述著同一事實的兩個方面，更高的風險意味著更低的可靠性[2]。提高可靠性可以降低系統的風險。如何有效地、快速地評估含風電電力系統的可靠性是一個重要的課題。

電力系統的可靠性評估主要分為確定性評估和概率性評估，其中概率性評估分為解析法和蒙特卡洛模擬法(MCS)[3]。MCS的優點在于，在計算精度一定的情況下，元件數目的多少不影響該方法的抽樣次數，且思路簡單，便于編程[4]。但是在MCS中，每一次狀態的分析和優化過程都占用了大量計算時間，隨著精度的上升和風電的并網，計算時間迅速增加。計算量與估計精度的平方成反比，因此，減少方差可以提高估計精度[5]。文獻[6]采用等分散抽樣減小方差，提高模擬精度，大幅減少了抽樣次數；文獻[7]將自適應重要抽樣應用在發輸電系統可靠性評估中，在元件故障概率較小時能顯著提高可靠性評估的計算效率；文獻[8]結合了重要抽樣和分層抽樣，提出分層均勻抽樣；文獻[9]采用重要抽樣改進拉丁超立方抽樣，提高抽樣效率；文獻[10-12]提出基于粒子群支持向量回歸法的電網可靠性評估的新方法，證明粒子群、支持向量機在電網可靠上的應用價值；文獻[13]提出交叉熵結合動態故障集，使用索引鏈表來記錄抽樣得到的故障和分析結果，通過查詢已經分析的樣本來減少重復分析，但沒有考慮風電場數量對計算時間的影響。

評估含風電的發輸電系統，需要建立風電場出力模型。文獻[14]以威布爾分布為基礎，考慮風電機組的尾流效應，建立了風電機組的三狀態模型。文獻[15]運用k-means聚類法處理風電場功率輸出時間序列，得到風電場出力的多狀態概率分布模型。

本文考慮風速的尾流效應，采用等分區間建立風電場的多狀態出力模型，提出分別采用紅黑樹、散列表這兩種數據結構來構造動態故障集，以包含數個風電場的IEEE-RTS79系統作為算例，分析兩種數據結構各自在計算時間上相對于MCS的優勢，并在不同的方差系數、風電場數量和風電場狀態數下，分別比較兩種數據結構在指標誤差、計算時間上的差異。

1 風電場的多狀態模型

本文通過蒙特卡洛模擬法獲得風電場出力，并將單個風電場的出力等效為多狀態發電機組。具體步驟如下：

步驟1：以威布爾分布建立風速模型，獲得風速序列；

步驟2：對風電機組建立正常、故障和降額三狀態模型，并進行序貫蒙特卡洛模擬；

步驟3：根據風電機組運行狀態和尾流效應，計算每個風速下，每臺風電機組的風速；

步驟4：通過各機組風速計算各機組的實際出力，從而獲得整個風電場的出力序列。

步驟5：風電場出力范圍均分為N個區間，每個區間的出力為該區間內出力的均值，每個區間的概率為該區間中出力的總持續時間與風電場出力持續總時間的比值。劃分完畢后就能獲得風電場的多狀態出力。

2 含風電場的發輸電系統可靠性評估

2.1 非序貫蒙特卡洛法

非序貫蒙特卡洛法又稱狀態抽樣法，其依據為：一個系統狀態是所有元件狀態的集合，每個元件狀態可由出現在該狀態的概率進行抽樣決定。對于一個兩狀態的元件i，其停運概率Pf、狀態Si可表示為

(1)

(2)

式中：λi和μi分別為元件i的停運率和修復率。

含m個元件的一個系統抽樣狀態為S=(s1,s2,…，sm)，當抽樣得到足夠數量，狀態S的抽樣頻率可作為其概率的無偏估計：

(3)

式中：NS為抽樣次數；n(S)為狀態S的次數。

指標的期望為

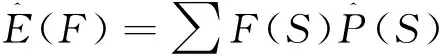
(4)

式中：F(S)為指標在狀態S下的值。

系統指標的不確定性可以通過樣本均值的方差度量，其定義為

(5)

式中：Fk為第k次抽樣得到的指標。

蒙特卡洛模擬的精度可以用方差系數描述，表示為

(6)

2.2 電力系統元件停運模型

電力系統常規元件包括輸電線、發電機等，這些元件通常采用正常、停運的兩狀態模型。負荷采用多級負荷模型。

2.3 最優切負荷

當電力系統中的元件停運或者風電場出力變化時，系統可能需要切負荷甚至發生解列。本文在調度發電機時，優先使用風電。最優切負荷模型如下：

目標函數為

(7)

約束條件為

PG-PD+PC=B0δ

(8)

(9)

PGimin≤PGi≤PGimax,i∈NG

(10)

0≤PCi≤PDi,i∈NB

(11)

|Pij|≤Pijmax,i,j∈NB

(12)

Pij=-bij(δi-δj)

(13)

式中：ND為帶負荷節點的集合；NG為帶發電機節點的集合；NB為所有節點的集合；PG為包括等效風電場在內的發電機出力向量；PD為有功負荷向量；PC為負荷削減向量；δ為節點電壓相角向量；B0為節點導納矩陣；PGi為節點i上發電機的有功出力；PCi為節點i上的切負荷；PDi為節點i上的有功負荷；PGimax、PGimin分別為節點i上發電機的出力上限和下限；Pij為支路ij的有功潮流；Pijmax為潮流上限；bij為支路ij的導納；δi為節點i的電壓相角。

3 動態故障集

使用動態故障集的主要目的為存儲狀態、查找狀態、避免重復分析狀態。MCS的每次抽樣能獲得該次的元件故障狀態和風電場出力，在不使用動態故障集時，需要對每次抽樣得到的狀態和出力都進行復雜繁瑣的分析，這些分析包括了檢查系統是否已經解列；負荷、發電是否平衡；進行簡單的潮流計算，并判斷是否有潮流或電壓越限；若有可能需要切負荷，則運行最優切負荷程序。最優切負荷程序約束眾多，即使采用了直流潮流和線性規劃，仍然會耗費大量計算時間。若為了減小誤差而采用交流潮流，則耗費的時間將更加龐大。因此，文獻[13]提出了采用動態故障集，即在MCS的計算過程中開辟一個內存空間，建立索引鏈表，將已經抽樣并分析的狀態和結果存儲在索引鏈表中，以索引鏈表的查詢來替代重復且費時的分析。在每次抽樣得到新的故障狀態后，首先查詢已存儲的狀態，若查詢成功，則直接讀取切負荷計算結果；否則對新狀態進行分析，并存儲結果。

在計算機數據結構中，數據的存儲和查詢除使用索引鏈表之外，更普遍的結構是紅黑樹和散列表。兩種數據結構均能實現高效地存取數據，但各有優劣，需要根據實際的應用場景進行選取。以下將分別介紹本文中數據的定義和這兩種結構的特點。

3.1 故障和失負荷信息的存儲結構

故障抽樣總次數為NS，第i次抽樣可以獲得一個故障狀態Si。Si為0、1組成的向量，由Si組成的故障狀態集合為稀疏矩陣。為節省內存空間，本文對每次抽樣中的m個元件從1到m依次編號，將編號存儲為向量FAULT以替代故障狀態Si，同時存儲故障階數NUM、數個風電廠的出力向量PW和切負荷信息CSTATUS。在MATLAB中定義類Data，包含成員變量FAULT、NUM、PW和CSTATUS。

3.2 基于紅黑樹的動態故障集

定義：一顆二叉樹若滿足如下性質，則稱為紅黑樹：

(1)每個節點不是紅色就是黑色；

(2)根節點為黑色；

(3)如果節點是紅色，則其子節點必須是黑色；

(4)任一節點至NULL(樹尾端)的任何路徑，所含黑節點數相同。

一顆以整數作為數據的紅黑樹結構如圖1所示。圖中，Data為節點的數據；Color為節點顏色，分別為紅色r和黑色b；Left和Right分別為指向左子樹和右子樹的指針，簡寫為L、R。

紅黑樹是一種平衡的二叉搜索樹，查找的時間復雜度小于O(log2N)，N為樹的節點數。平衡的大致意義是沒有任何一個節點深度過大。普通的二叉搜索樹的查詢效率與樹的深度有關，當左右子樹的深度差較大時，查詢效率與鏈表(時間復雜度O(N))接近。包含紅黑樹在內的平衡二叉樹，在插入和刪除節點時耗時較長，但是可以避免高度不平衡的情況，一般而言搜索時間可以節省25%左右。

紅黑樹的查找、插入和刪除等基本操作詳見文獻[17]。紅黑樹的構造要求節點中的Data是有序的。如果Data為數，則對于任意一個節點，其左子節點中的數總是小于右子節點的數。因此需要在MATLAB中為類Data定義順序，按以下步驟確定節點大小：對于任意的節點甲和乙：

(1)若節點甲的NUM小于節點乙，則節點甲更小；

(2)若節點甲的NUM大于節點乙，則節點甲更大；

(3)若節點甲的NUM等于節點乙，則繼續比較PW，轉步驟(4)；

(4)依次比較PW的各個風電場的出力大小，若完全相等，則繼續比較FAULT，轉步驟(7)；

(5)若先發現節點甲PW的元素更大，則節點甲更大；

(6)若先發現節點甲PW的元素更小，則節點甲更小；

(7)依次比較FAULT的各個故障編號的大小，若完全相等，則兩個節點完全一致；

(8)若先發現節點甲FAULT的元素更大，則節點甲更大；

(9)若先發現節點甲FAULT的元素更小，則節點甲更小。

如圖2所示為本文紅黑樹節點的結構。

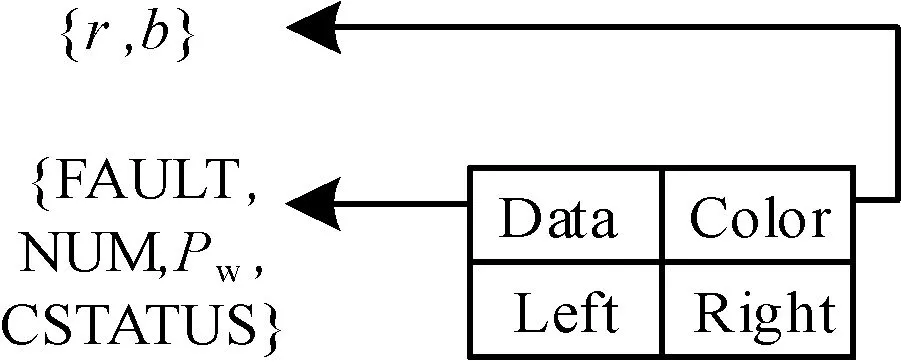
圖2 紅黑樹節點的結構

3.3 基于散列表的動態故障集

常用的數據搜索方式除了紅黑樹外，還有散列表(Hashtable)，又稱哈希表。如圖3所示為散列表的結構。

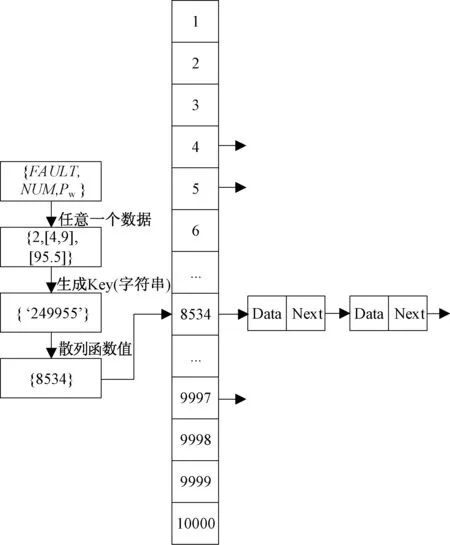
圖3 散列表的結構

散列表現為常數平均時間，時間復雜度為O(1)。散列表可以看作數組，對某個數據項的訪問和其他數據項完全獨立。為了訪問某個數組元素，需要定義數據data的鍵(key)，使用散列函數將鍵作為實參，并返回一個指明元素位置的整數值。散列表不需要知道Data的順序和大小，不會有類似紅黑樹的排序所消耗的時間，但會多出計算散列函數的時間，各有利弊。本文將Data轉換為字符串作為鍵，所用的散列函數參考文獻[16]，并使用拉鏈法來解決不同的數據項映射到相同的位置的問題。不同的故障和風電場出力將會有不同的散列函數值，但也存在不同的Data計算得同一值的可能性，即產生沖突。拉鏈法通過單鏈表，將沖突的故障存放在單鏈表中。

4 算例分析

本文使用IEEE-RTS79測試系統，該系統包括24個節點，32臺發電機，38條線路，總裝機容量 3 405 MW，年負荷峰值2 850 MW，電氣接線如圖4所示，測試系統的線路、發電機的強迫停運率和負荷數據見文獻[1]。風電場布局見文獻[14]，相鄰風機水平距離為350 m，垂直距離為850 m。每個風電場包含風電機135臺，分為9組，每組為一行，一組15臺風電機。每臺風電機額定功率取1.2 MW，停運率取0.05，降額率取0.05，停運修復率58.4，降額恢復率43.8，葉輪高60 m，葉片半徑37 m。威布爾分布的形狀參數取2.02，尺度參數取8.03。切入風速3 m/s，切出風速25 m/s，額定風速12 m/s。風電場接入節點設置為系統的23節點。評價指標選取為電量不足期望(EENS)和切負荷概率(LOLP),收斂條件為EENS的方差系數η。

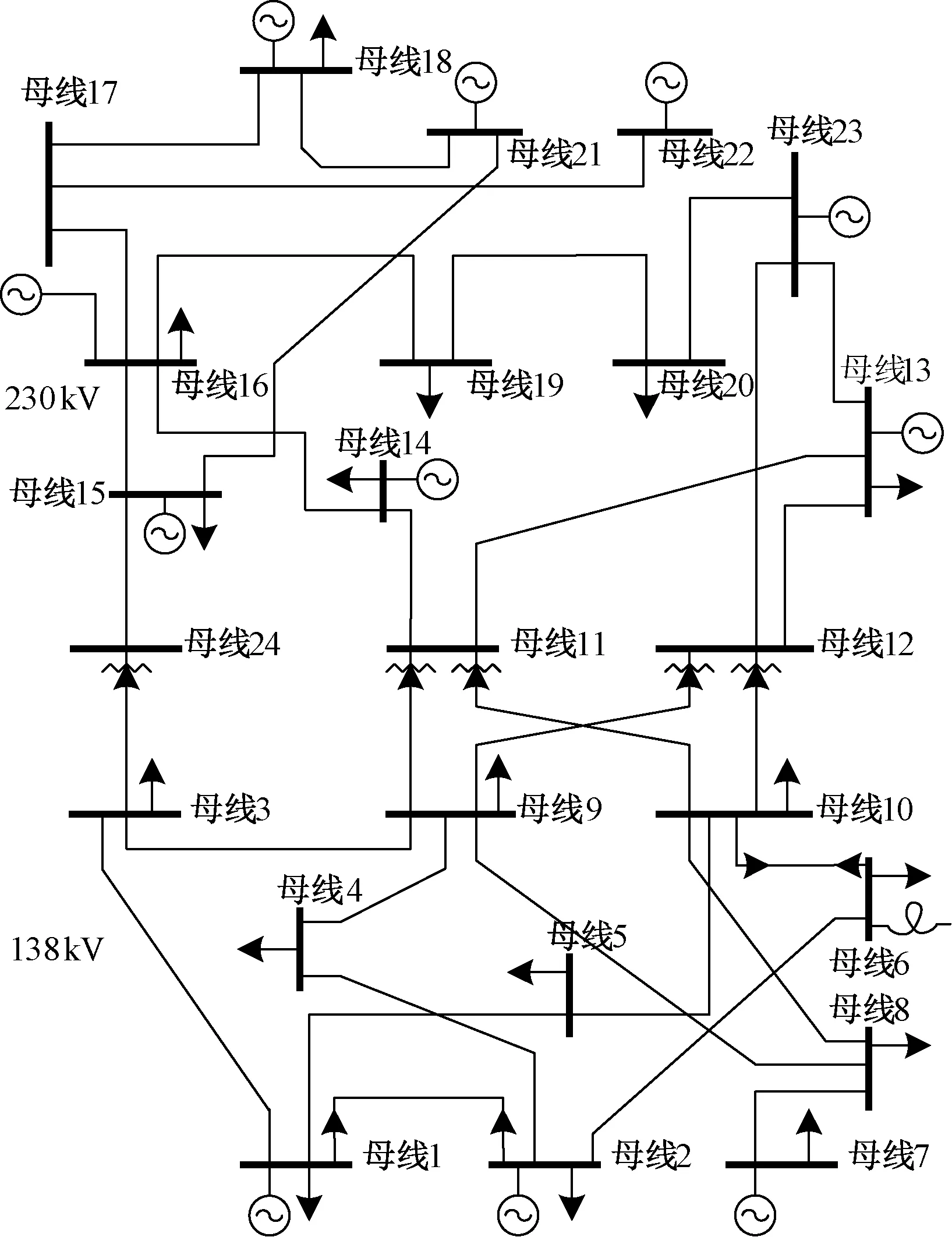
圖4 IEEE-RTS79電氣接線圖

4.1 3種方法的評估結果和計算時間對比

表1所用系統的風電場數量為1、風電場出力等效狀態數為5，η為0.1，將未采用動態故障集的MCS方法和采用紅黑樹、散列表的方法進行對比，分析在迭代次數、指標、計算時間上的差異。由表1可知，在約20 000次左右的抽樣次數下，采用紅黑樹后的計算時間僅為MCS的22.89%，采用散列表后的計算時間僅為MCS的21.02%，可見使用動態故障集后，顯著提高了可靠性評估的速度。紅黑樹的指標EENS相對MCS方法的指標偏離了4.37%，散列表偏離了5.39%，均小于方差系數的10%，都在可接受的范圍之內。紅黑樹的指標LOLP相對MCS方法的指標偏離了5.02%，散列表偏離了5.19%，也相差不大。因此，在合適的條件下，采用紅黑樹或采用散列表的動態故障集均能夠有效改善含風電電力系統的可靠性評估速度，并對評估指標的誤差影響不大。

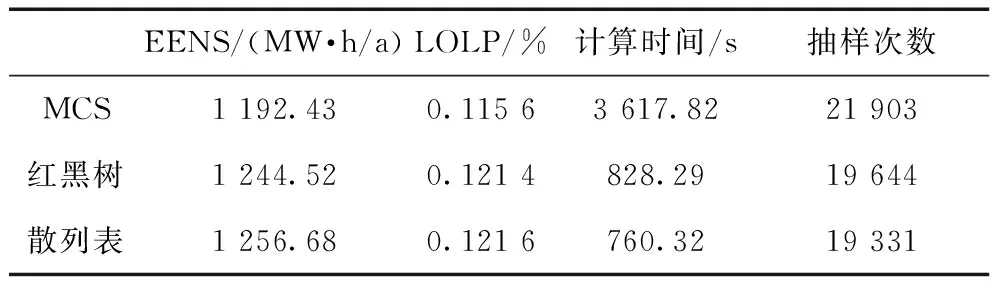
表1 3種方法的評估指標和計算時間

4.2 風電場數量對計算時間的影響

增加風電場的數量，系統的23節點上變為3個同樣規模的風電場，風電場等效狀態數保持為3個，η保持為0.1，結果見表2。

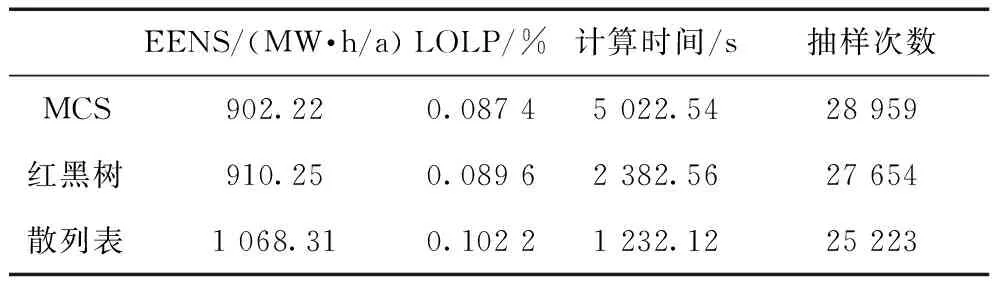
表2 有3個風電場時的評估指標和計算時間

在表2中，散列表的時間為MCS的24.53%，比表1中的21.02%大，這是由于風電場數量增加的影響，轉換得到的字符串變長，相應的散列函數的計算時間也更長。對比表1的結果，能發現隨著風電場數量的增加到3個，MCS的時間增加了38.83%，紅黑樹的時間增加了87.65%，散列表的時間增加了62.05%。紅黑樹的計算時間增幅最大。主要原因是：紅黑樹在查找時需要根據Data為新舊節點排序，隨著Data中風電場出力向量PW長度的增加，使得大量時間耗費在風電場出力大小的比較上，而散列表的散列函數受此影響更小。

雖然散列表的時間更短，但是表2散列表的結果中，指標EENS偏離MCS達到18.41%，LOLP的偏離也達到16.93%，可能的原因為Data到key的轉換函數和散列函數在設計上存在不足。隨著樣本規模擴大，散列沖突愈發嚴重。因此，在包含風電的電力系統可靠性評估中，隨著所需記錄的數據種類與數量變多，設計合適的散列表和散列函數可以比需要排序的紅黑樹實現更快的查詢，但也面臨著無法預知采用何種key轉換函數和散列函數更優的問題。

本文考慮的是大型風電場，因此數量不會太多，只討論到單個節點上最多10個風電場。圖5為隨著風電場數量增加，紅黑樹方法和MCS的計算時間的變化，以及紅黑樹方法占兩者總時間比例的變化，圖6為兩者抽樣次數的變化。由圖5中兩種方法各自的變化趨勢可見，風電場總數越多，則計算時間的增幅越大；在風電場數量增加到4個或更多之后，紅黑樹相對MCS的時間優勢基本上保持在60%到70%，沒有繼續劣化。

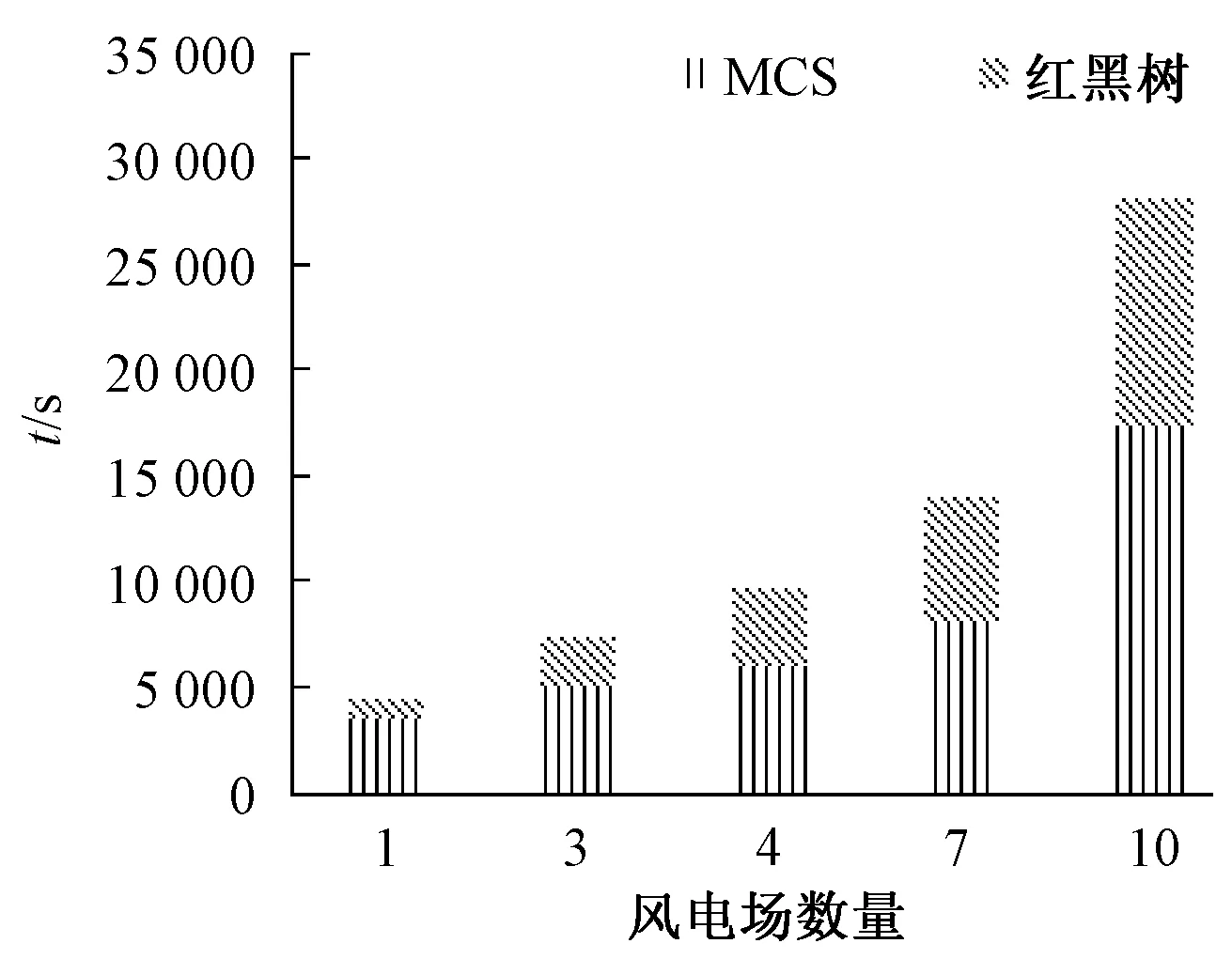
圖5 風電場數量對紅黑樹計算時間的影響

由圖6可知，當風電場數量增加到4個以上，紅黑樹相比MCS總是以更少的抽樣次數就能滿足方差系數，因此盡管之前的分析中紅黑樹性能明顯受到風電場數量增加的影響，但MCS抽樣次數的增速大于紅黑樹，因此最終紅黑樹的計算時間占總時間的比例穩定在60%～70%。

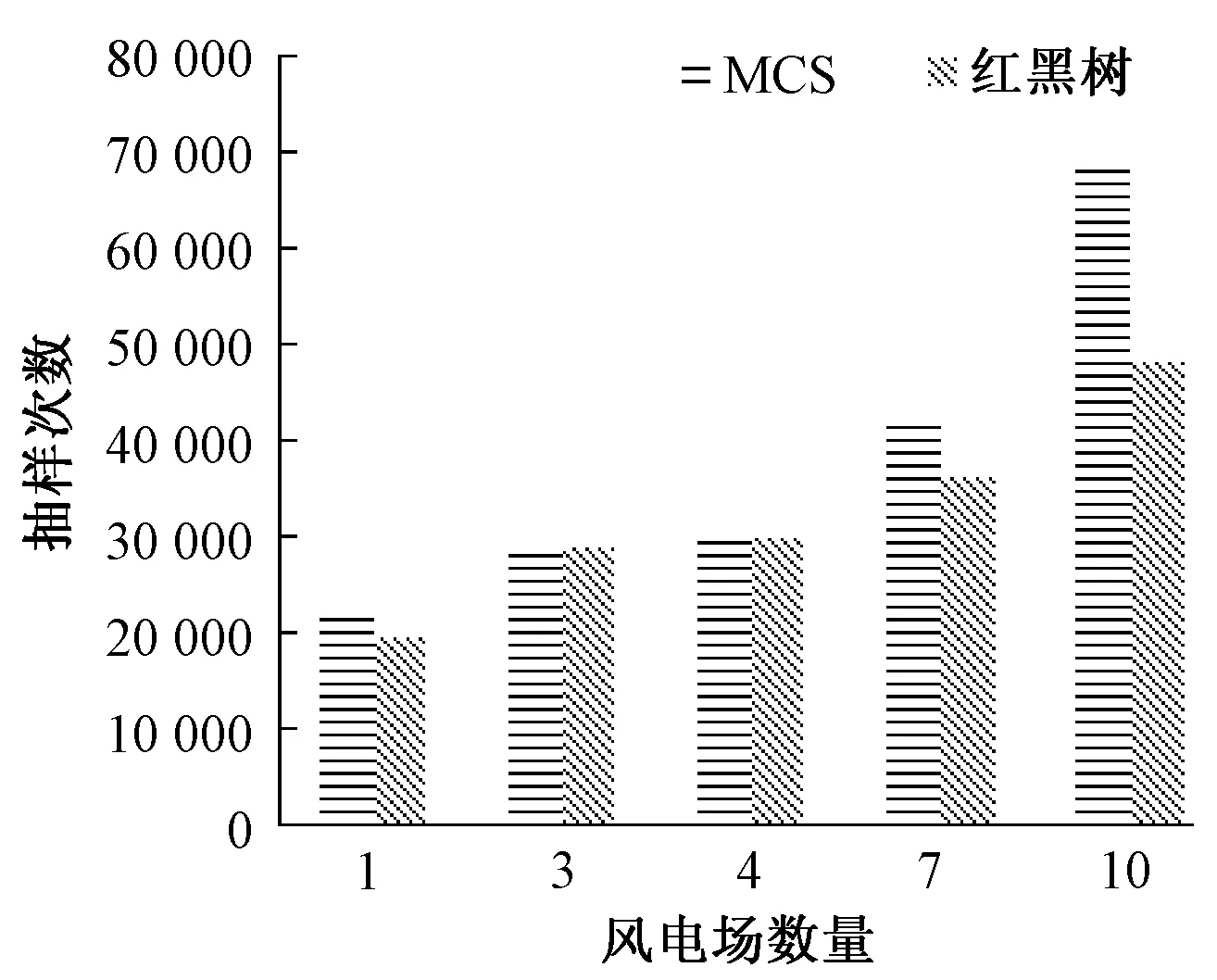
圖6 風電場數量對紅黑樹抽樣次數的影響

4.3 風電場狀態數對計算時間的影響

表3中，η保持為0.1，風電場數為1。對比表1，在風電場等效狀態數增加后，抽樣次數顯著較少，使得3種方法的計算時間均顯著減少。紅黑樹、散列表相對MCS的時間分別為24.22%、23.81%，與表1中的結果相差很小。與風電場數量增加時不同，風電狀態數并沒有使紅黑樹性能明顯下降，風電狀態數與紅黑樹和散列表的性能關系不大。

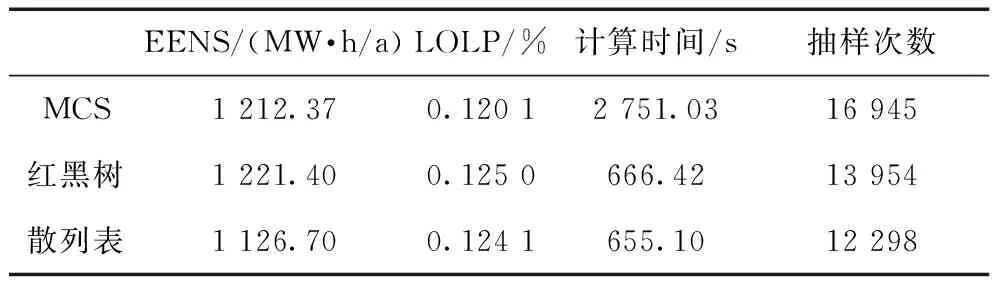
表3 風電場狀態數為10的評估指標和計算時間

4.4 精度對計算時間的影響

對不同精度下的計算時間進行比較，風電場數量為1，風電場出力等效狀態數為5，結果見表4。表4列出了不同精度下，紅黑樹、散列表各自相對MCS的時間比。在抽樣次數上，3種方法相差不多。在方差系數減小到0.075時，紅黑樹和散列表的時間比最高，接近30%。而當方差系數減小到0.05時，紅黑樹和散列表的時間比減少到20%。可見，在由計算精度導致的規模增大時，紅黑樹和散列表都能夠維持不錯的減時的效果。散列表的散列沖突依然存在，且在不同的精度下，EENS偏離程度不一，精度0.1時偏離了5.39%；精度0.075時，偏離了23.27%；精度0.05時偏離了3.84%。

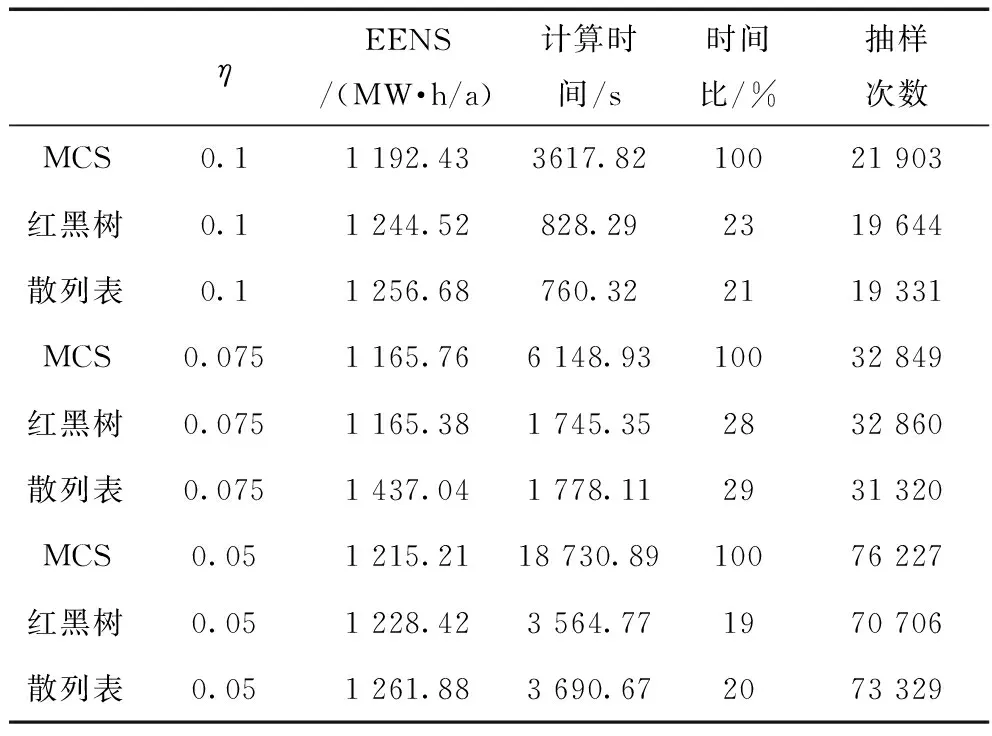
表4 不同精度下的評估指標和計算時間

當計算精度繼續增加，故障集的規模迅速擴大，精度小于0.05時，需要數十萬次以上的迭代。散列表和紅黑樹的計算時間在不同的故障集規模下始終保持一致。從計算時間的絕對值差上看，相對于MCS，紅黑樹和散列表節省的時間會隨著故障集規模的增大愈發突出。

5 結論

本文提出采用紅黑樹優化的動態故障集，加速傳統非序貫蒙特卡洛法的計算速度。同時對比了采用散列表優化的動態故障集。在包含數個風電場的IEEE-RTS79測試系統中進行算例分析，得到以下結論：

(1)采用了紅黑樹的動態故障集與采用散列表的動態故障集在蒙特卡洛模擬中的應用使得計算時間顯著下降80%左右；

(2)當風電場數量較多時，紅黑樹的加速效果會明顯下降，但依然優于MCS，散列表的加速效果保持不變；

(3)風電場等效狀態數對紅黑樹、散列表加速效果的影響不明顯。風電場等效狀態數增加能夠顯著減小抽樣次數，使得MCS的計算時間減少。

(4)散列表雖然理論查找性能強于紅黑樹，但是受到散列函數的制約，散列函數的計算時間使得散列表的實際查找性能不一定優于紅黑樹。當預先設計的散列函數和key轉換函數不合適時，會導致難以預期的散列沖突，使可靠性指標偏離正確值。

參考文獻：

[1]蔣程，劉文霞，張建華，等．含風電接入的發輸電系統風險評估[J]．電工技術學報，2014，29(2)：260-270．

[2]黃旭．含異步化同步發電機的電網可靠性評估模型研究[D]．重慶：重慶大學，2012．

[3]杜江．基于蒙特卡洛法的電力系統可靠性評估算法研究[D]．杭州：浙江大學，2015．

[4]張巍峰．基于蒙特卡洛法的電力系統可靠性評估算法研究[D]．天津：天津大學，2014．

[5]王立雪，孫聚波，徐平峰．蒙特卡羅方法及其方差縮減技術比較分析[J]．長春工業大學學報，2015，36(5)：485-490．

[6]陳文婕，劉晉，周云海，等．基于等分散抽樣法的配電系統可靠性評估[J]．陜西電力，2010，38(6)：23-27．

[7]謝紹宇，王秀麗，王錫凡，等．自適應重要抽樣技術在發輸電系統可靠性評估中的應用[J]．電力系統自動化，2010，34(5)：13-17．

[8]黃江寧，郭瑞鵬，趙舫，等．電力系統可靠性評估中的分層均勻抽樣法[J]．電力系統自動化，2012，36(20)：19-24．

[9]張巍峰，車延博，劉陽升．電力系統可靠性評估中的改進拉丁超立方抽樣方法[J]．電力系統自動化，2015，39(4)：52-57．

[10]王景辰，李孝全，楊洋，等．基于蒙特卡洛法和最小二乘支持向量機的復雜電力系統可靠性評估[J]．華東電力，2013，41(5)：1001-1004．

[11]龔蘭芳，張昱．電網可靠性評估的PSO-SVR評估模型[J]．計算機仿真，2011，28(7)：196-199．

[12]李孝全，黃超，徐晨洋，等．基于改進PSO-LSSVM和蒙特卡洛法的電力系統可靠性評估[J]．河海大學學報(自然科學版)，2016，44(5)：458-464．

[13]許鵬程，陳啟，劉文霞，等．引入交叉熵與動態故障集的含風電大電網可靠性評估[J]．電力系統自動化，2016，40(13)：28-34．

[14]張碩，李庚銀，周明．含風電場的發輸電系統可靠性評估[J]．中國電機工程學報，2010，30(7)：8-14．

[15]仇國兵．基于聚類的復雜地形下風電場輸出功率概率分布建模[D]．北京：華北電力大學，2014．

[16]鄧俊輝．數據結構:C++語言版．第2版[M]．北京：清華大學出版社，2012．