基于海量用電數據的用戶負荷模式快速提取方法研究

盧錦玲， 馬 沖， 馮翠香

(華北電力大學 電氣與電子工程學院，河北 保定 071003)

0 引言

隨著智能電表的普及和數量的日益增多，由大規模智能電表采集得到的用電數據不僅具有大數據的4 V特點(volume, variety, velocity and value),還具有電力系統特有的3E特點(energy, exchange and empathy)[1]。對海量用戶用電數據的有效分析不僅可以滿足負荷預測、風險預警、異常檢測、負荷模式提取、優化生產調度、需求響應分析等[2-4]的基礎工作，還可以科學地提高電網自動化水平，從而實現電網可靠、安全、經濟、高效、和諧友好和用電安全的環境。

對負荷模式的有效提取對應用于負荷控制、負荷預測、風險預警、分時電價的制定與實施、用電異常檢測等[5-10]具有重要的指導作用，負荷模式提取的準確性很大程度上影響后續工作的穩定進行。目前國內外對用電大數據的負荷模式提取研究，已成為當下熱點課題[11-14]。文獻[6]利用云計算強大的數據存儲及并行計算能力，進行Map-Reduce并行處理模型下基于改進K-means算法的海量用戶用電數據并行挖掘。文獻[7]針對單一聚類算法的不足，研究基于經典聚類算法的集成算法，并將其應用于負荷曲線聚類，最后結合主成分分析降維方法對高維數據進行降維。文獻[12]利用K-means算法具有收斂速度快、效率高的優勢，采用了改進K-means算法對用戶進行聚類，并根據模型對負荷需求進行預測。文獻[15]提出了一種函數型聚類分析方法，利用K-means聚類算法，對海量電力用戶稀疏、不規律的日耗電量數據進行特征分析，并對用戶進行分類。文獻[16]利用基于聚類有效性修正的德爾菲方法配置特性指標權重，提出一種特性指標降維的日負荷曲線聚類方法。但在聚類過程中，由于聚類中心點的隨機選取使得聚類結果穩定性不高。文獻[17]利用改進K-means聚類算法，并結合有效指標準則，能夠有效地提取出日負荷曲線，但該方法需要遍歷所有聚類數K，以得到最優聚類數，使得算法效率不高。

由此可以看出，國內外對海量負荷模式的提取主要集中在對算法的改進和大數據處理效率方面[8-12]，其聚類可靠性高，處理大數據時有顯著優勢，但是對數據清理方面所做工作較少，往往使得修正后數據準確率有待提高，此外，在對用戶更細粒度的聚類研究較少，當用戶種類較多時提取最優負荷模式所用時間較長。

針對上述問題，本文首先考慮到用電大數據的分布特點，將四分位法與3σ法相結合，提出一種“橫向—縱向”法來對異常用電數據檢測與修正，以提高數據修正的速率與準確率；其次，綜合對比了幾種典型的數據降維方法，得出用主成分分析法對海量用電數據進行降維后將極大地提高負荷模式提取效率；最后，在傳統K-means算法簡單快速優勢的基礎上改進得到Fast K-means(FK-means)算法，該算法利用二分法思想來減小聚類時間，將聚類有效性指標DBI與CHI相結合來提高聚類結果可靠性，該算法不僅具有魯棒性好，對負荷模式提取速率快的優勢，并且隨著電力用戶種類的增多，效果提升更明顯。

1 負荷模式提取流程

本文將從負荷模式提取的各個步驟來詳細介紹，具體流程如圖1所示。對負荷模式提取的步驟如下：

(1)對采集得到的用戶用電數據進行異常值處理：包含離群點和空缺值，并對處理后的數據進行歸一化處理。

(2)對數據進行降維處理。

圖1 FK-means算法對負荷模式提取流程圖

(3)采用FK-means算法進行聚類，快速確定最優聚類數所在區間，并計算最優聚類數所在區間中DBI與CHI指標，從而得到max{CHIK-DBIK}，K即為對應的最優聚類數。

(4)對數據還原，從而得到聚類后的用戶用電特性曲線。

2 數據處理

2.1 數據預處理

由于用電數據在橫向上具有相似性，短時間間隔內(本文處理的用電數據采集時間間隔為30 min，每個用戶采集30天)在縱向上具有無突變性的特點，而且用電數據為單一屬性數據。本文根據用電數據的分布和屬性特點，提出一種“橫向—縱向”法來辨別修正異常用電數據。

由于用電數據的橫向相似性，在橫向上利用四分位法簡單快速的優勢來對異常用電數據進行初步定位，其定義如下。

(2)其中前25%為上四分位用FL表示，后25%處于下四分位用FU表示。四分位數間距為：dF=FU-FL，上截斷點為：Q1=λdF-FL，下截斷點為：Q2=FU+(1-λ)dF。

(3)其中小于Q1或者大于Q2的數據將其初步定為異常用電數據。

上式參數λ取值0.5～1，本文λ取為0.85。

在橫向上用四分位法對用電數據進行粗辨識后，利用短時間間隔內用電數據在縱向上無突變性的特點，對初步篩選出的異常用電數據在縱向上用3σ法的精確性對其進一步辨別并修正，其定義如下。

(1)

(2)

(3)

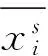
凡滿足式(3)的均為異常用電數據，將異常用電數據用其所在時刻的其他樣本點的平均值來代替。

2.2 數據歸一化

對用電數據進行處理后，取各用戶月數據(不含周末)平均值作為典型日負荷曲線，每條負荷曲線表示為xi={xi,j,j=1,2,…,n}，由于每個負荷樣本具有不同的最大最小負荷，為了后續方便分析，采用如下的方法進行數據歸一化:

(4)

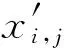
3 降維處理

對用電數據進行處理后得到的用戶典型日負荷曲線仍具有維度高的特點，使得后續聚類耗時較長。為了對海量用戶進行負荷模式提取時能夠進一步提高效率，有必要對高維數據進行降維處理，降維的目的是用較低維數的向量來表示負荷曲線。降維不僅能夠節約數據的存儲空間，還能夠減少計算時間，提高算法效率。本節對當下主流的無監督降維方法進行對比分析，從而選取一種最優降維方法。

3.1 降維方法

常用的無監督降維方法有主成分分析PCA、局部保持投影LPP、特征值提取FE[18]等。

(1)主成分分析PCA(Principal Component Analysis, PCA)

PCA的目標是通過某種線性投影，將高維的數據映射到低維的空間中表示，并期望在所投影的維度上數據的方差最大，以此使用較少的數據維度，同時保留住較多的原數據的特性。目標函數定義如下：

E(S)=STPTS

(5)

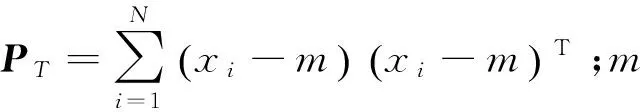
考慮到約束條件STS=1，利用拉格朗日乘子法，構造拉格朗日函數為：

L(S,φ)=STPTS-φ(STS-1)

(6)

式中：φ為拉格朗日乘子；對式(6)中S求偏導，令偏導數為零，之后便轉化為求ST特征值的問題，將前d個最大的特征值組成投影矩陣，從而將高維數據通過投影矩陣映射到d維上。

(2)局部保持投影LPP(Locality Preserving Projections, LPP)

LPP是能夠保護數據中的簇結構的線性降維方法。設yi為xi的一維描述，其目標函數如下：

(7)

式中：A為投影降維矩陣；相似度矩陣W=[Wij]N×N為對稱陣，矩陣內部元素定義為：

(8)

式中：參數δ0等于總體樣本方差；xi∈N(xj)表示xi與xj相鄰。

從該方法的權值矩陣S的設置中可以看出，其在對應近鄰樣本的位置上賦了一個非零權值，而對于相距較遠的樣本則賦零。這樣就可以在投影中，達到保留樣本的近鄰結構的目的。

(3)特征值提取FE(Feature Extraction, FE)

特征值提取法是對每條負荷曲線提取特性指標，本節采用6種特性指標，分別為：日負荷率、最高利用小時率、日峰谷差率、峰期負載率、平期負載率、谷期負載率。

3.2 降維結果分析

在原始數據保留度相同的情況下，對部分樣本采用上述降維方法進行降維，對比結果如圖2所示。

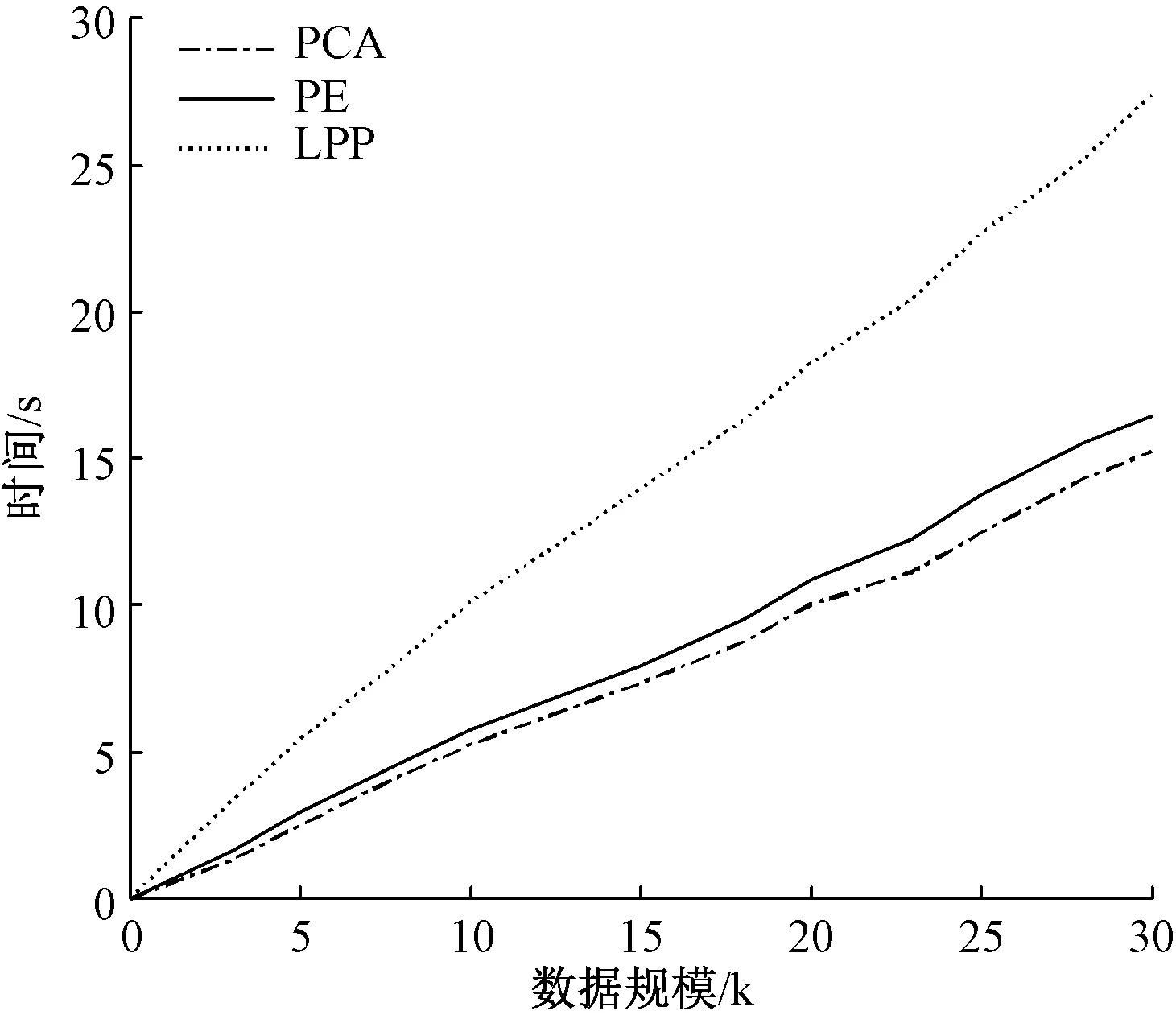
圖2 各種降維算法計算時間

從圖2可以看出，隨著數據量的增加，LPP用時最多，PCA用時最少，且數據量越大越明顯，故選用主成分分析PCA來對樣本數據進行降維。

4 負荷模式提取

傳統K-means算法具有簡單、收斂速度快的優勢，其時間復雜度為O(KNT),其中K為聚類數，N為樣本總數，T為迭代次數。但傳統K-means算法有兩點不足：聚類數K與初始聚類中心需要事先確定。本節將介紹FK-means算法如何減小聚類時間并提高穩定性。

4.1 聚類有效性指標

聚類有效性是通過建立有效性指標，評價最佳聚類質量并得到最佳聚類數的過程，當數據的原始正確劃分未知時，采用內部評價指標。常用的內部評價指標有DBI(Davies-Bouldin Index)指標、XBI(Xie-Beni Index)指標、CHI(Calinski-Harabasz Index)指標和PBM指標[19]。其定義分別如下。

(1)DBI指標

(9)

式中；Ci為類簇i所構成的集合；Wi表示類Ci中的所有樣本到其聚類中心的平均距離；∣Cij∣表示類Ci與Cj中心之間的距離?？梢钥闯鯠BI指標越小表示類與類之間的相似度越低，同一類內的相似度越高，從而對應的聚類數越佳。Wi與∣Cij∣表達如下：

(10)

式中：ni表示類Ci中樣本數據xi的個數；Zi為類Ci中心點。

(11)

(2)XBI指標

(12)

式中：μij是一個布爾值。當xj屬于第i類時，μij為1，否則為0。分子表示屬于同一類簇的樣本到其類簇中心的距離，衡量緊密性；分母表示不同類簇中心之間的距離，衡量分離性，因此XBI值越小，聚類效果越好。

(3)CHI指標

(13)

式中：類內離差WGSS定義如下：

(14)

類間離差BGSS定義如下：

(15)

式中：Z為整個樣本集的中心。

該指標分母衡量類內緊密性，分子衡量類間分離性，因此CHI指標越大聚類效果越好。

(4)PBM指標

(16)

式中：DB表示樣本中類簇中心間的最大距離，即：

(17)

式中：EW表示樣本中每個類簇內的所有點到該簇質心的距離之和，即：

(18)

式中：ET表示樣本中所有點到整個樣本集中心的距離之和，即：

(19)

PBM指標越大，聚類效果越好。

4.2 聚類指標分析

本次實驗數據取自SEAI發布的愛爾蘭智能電表實際量測數據，采集頻率為30 min，實驗數據包含24 611條負荷曲線。對實驗數據進行處理并聚類，聚類所得的各聚類指標與聚類數的關系如如圖3所示。

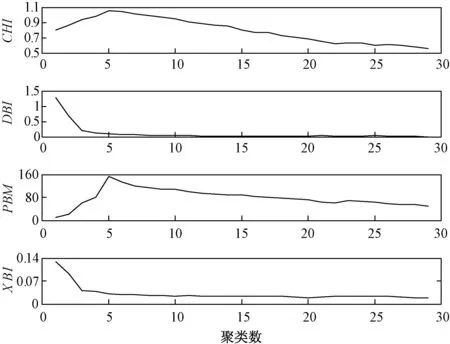
圖3 各聚類指標與聚類數的關系

從圖3可以看出，4種聚類指標隨著聚類數目的增加都有一個最大轉折點，即為對應的最優聚類數。不同的是，PBM指標數值較大，而XBI指標數值較小，若作為評價指標使用則對比效果不明顯，此外，若采用單一聚類指標評價聚類結果，則可靠性不高。由于CHI與DBI指標特點具有互補性，且指標數值較為接近。故本文采用CHI與DBI指標相結合的方法，以提高聚類結果的準確性和穩定性。

4.3 聚類數的確定

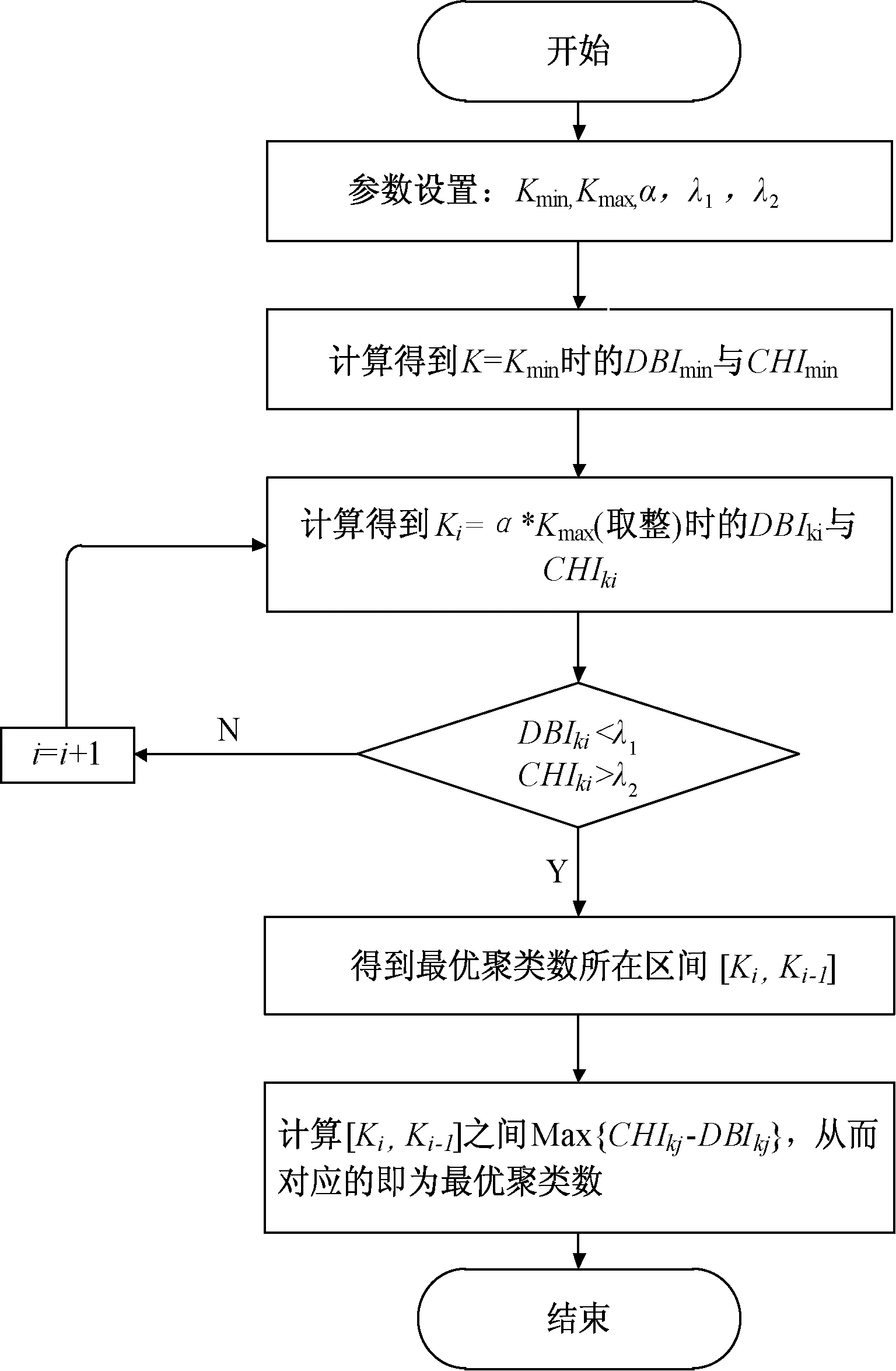
圖4 FK-means聚類

根據CHI與DBI指標的特點，λ1取0.5,λ2取0.9。本文α取0.8。

4.4 聚類中心的確定

由于隨機確定初始聚類中心，使得傳統K-means穩定性不高。為了解決上述問題，本文采用基于“最大最小距離”法來確定初始聚類中心，即初始聚類中心相距盡可能遠，避免了初始聚類中心過于臨近而陷入局部最優，從而獲得更高質量的聚類。“最大最小距離”法原理如下：

(1)先從總樣本數據集X={x1,x2,…,xN}中隨機挑選一個xi作為初始中心點A。

(2)計算余下數據集中每個樣本點與初始中心點A的距離，選取距離最大的樣本點作為中心點B。

(3)再計算余下數據集中每個樣本點與各個中心點的距離distiA與，得到兩個中心距離中最小的點min{disti,A,distiB}，再從所有樣本點的距離中找到最大的距離,此樣本點作為下一個中心點C。迭代條件滿足：

式中：distiA為樣本點xi與中心點A之間的距離；distiB為樣本點xi與中心點B之間的距離；distiC為樣本點xi與中心點A、B距離的最小值；DistiC為樣本點xi中所有最小距離中的最大值。

(4)重復步驟3，直到選取K個中心點。

以上是初始聚類中心的選取原則，在之后迭代中，聚類中心取聚類后類間距離的平均值作為新的聚類中心。當聚類中心不再發生變化時，則迭代結束算法收斂。

5 算例分析

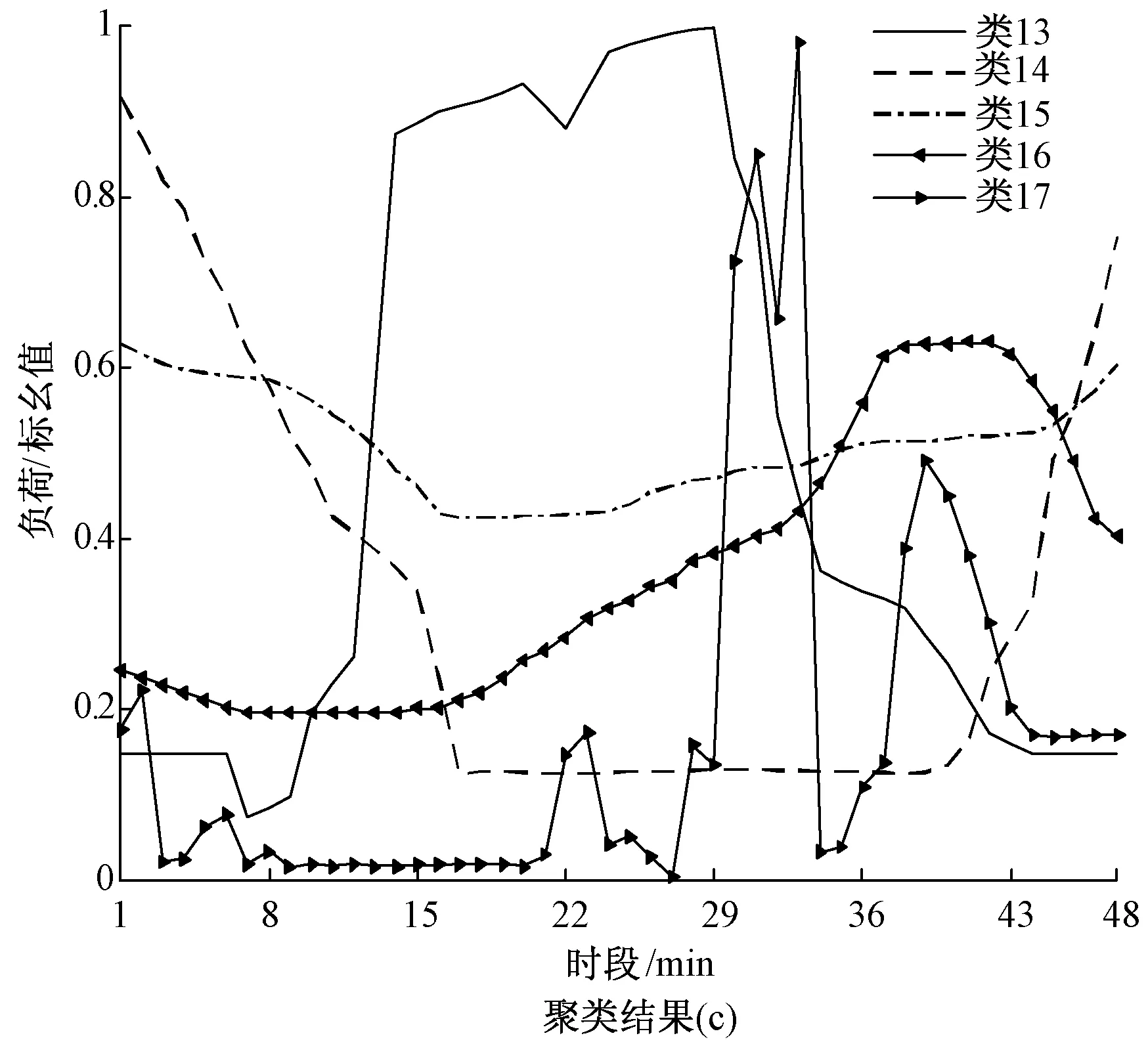
圖5 用戶日用電模式結果

5.1 負荷模式提取效率分析

為便于直觀分析，用典型用電曲線代表所在類簇的負荷，將典型用電曲線進行類比，得到的用戶日用電模式結果如圖5所示。

從圖中可以看出，類1、類7、類8、類9、類11、類14和類16在晚間用電量大，此類用戶多為娛樂消費場所或寫字樓等；類2、類4、類5午和類13午間用電量大，此類用戶多為居民用電或醫院學校等；類3,、類6、類10和類15用電較為平緩，但是用電量有所差異，此類用戶多為商業或工業等用電，并根據用電量的大小可以劃分商業或工業規模的大??；類12和類17用電波動較大，此類用戶多為農業用電。

用FK-means算法對數據集聚類所用的時間為1 104.59 s。而將最大聚類數Kmax設定為80時，采用傳統K-means法來進行負荷模式提取，用傳統K-means算法對數據集進行聚類后所用時間為 4 634.83 s。可以看出，FK-means算法相較于傳統K-means算法計算時間大幅降低，并且隨著用戶種類的增多，FK-means算法這一優勢越明顯。

用FK-means算法分別對降維前后的用電數據進行負荷模式提取，其中對降維后的負荷模式提取耗時306.37 s，而對未降維的用電數據進行聚類所需時間為1 104.59 s，可見結合降維技術的FK-means算法在對負荷模式提取時效率更高。

5.2 負荷模式提取可靠性分析

K-means算法對負荷模式進行提取時異常用電數據直接進行刪除，而FK-means算法采用“橫向—縱向”檢測法來對異常用電數據進行修正。從37 611個用戶數據中選取部分數據進行對比驗證。兩種情況下的聚類差異性如表1所示。

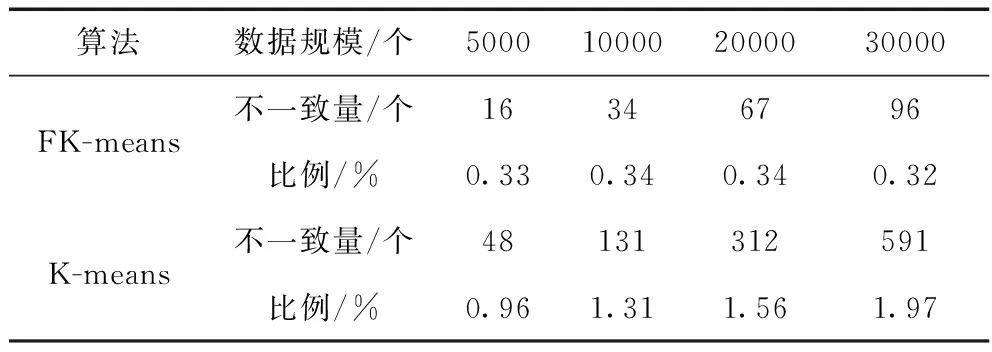
表1 FK-means算法與K-means算法聚類結果差異比較

從表1可知，FK-means算法比K-means算法聚類所得結果可靠性更高，由于K-means算法對異常用電數據直接進行刪除，隨著異常用電數據的增加，其對聚類產生的影響越明顯，得到的結果越不可靠，此外，由于傳統K-means是隨機產生初始聚類中心，使得聚類結果易陷入局部最優，無法得到高質量的聚類。而FK-means算法在經過“橫向—縱向”法對異常用電數據修正之后，其對整體聚類結果所產生的影響可以忽略，并且消除了初始聚類中心的隨機性問題，從而使得聚類結果更穩定，算法魯棒性好。

6 結論

本文提出了一種FK-means算法的電力用戶用電特性快速提取法。

(1)本文采取一種“橫向—縱向”檢測法，來檢測并糾正異常用電數據，首先利用四分位法簡單快速的優勢，初步確定異常用電數據點，然后利用3σ法的精確性，對初步確定的異常用電數據進一步檢測并修正。

(2)對于海量的高維負荷曲線，本文對比了幾種常用的降維方法，從而得出主成分分析法用時最短，效率最高。

(3)為了降低負荷模式提取所用時間，本文利用二分法思想來快速確定最優聚類數范圍，極大地減小了聚類時間。為了提高負荷模式提取結果的可靠性，本文對比了幾種常用的聚類有效性指標，采用DBI與CHI指標相結合的方法，兩種指標相結合使得聚類結果更穩定更準確。

(4)本文提出的FK-means算法能夠快速準確的確定最優聚類數，相較于傳統的K-means算法，FK-means算法能夠顯著減小聚類時間，魯棒性好，并且對處理大數據具有很大優勢。

參考文獻：

[1]DEFU C. Electric power big data and its applications[A]. Science and Engineering Research Center. Proceedings of 2016 International Conference on Energy, Power and Electrical Engineering (EPEE2016)[C]. Science and Engineering Research Center, 2016: 4.

[2]王桂蘭, 周國亮, 趙洪山, 等. 大規模用電數據流的快速聚類和異常檢測技術[J]. 電力系統自動化, 2016, 40 (24): 27-33.

[3]宋亞奇, 周國亮, 朱永利. 智能電網大數據處理技術現狀與挑戰[J]. 電網技術, 2013, 37 (4): 927-935.

[4]張素香, 趙丙鎮, 王風雨, 等. 海量數據下的電力負荷短期預測[J]. 中國電機工程學報, 2015, 35 (1): 37-42.

[5]馮麗, 邱家駒. 基于電力負荷模式分類的短期電力負荷預測[J]. 電網技術, 2005 (4): 23-26.

[6]趙莉, 候興哲, 胡君, 等. 基于改進k-means算法的海量智能用電數據分析[J]. 電網技術, 2014, 38 (10): 2715-2720.

[7]張斌, 莊池杰, 胡軍, 等. 結合降維技術的電力負荷曲線集成聚類算法[J]. 中國電機工程學報, 2015, 35 (15): 3741-3749.

[8]王德文, 周昉昉. 基于無監督極限學習機的用電負荷模式提取[J/OL]. 電網技術， 1-8[2017-12-24].https://doi.org/10.13335/j.1000-3673.pst.2017.1644.

[9]趙巖, 李磊, 劉俊勇, 等. 上海電網需求側負荷模式的組合識別模型[J]. 電網技術, 2010, 34 (1): 145-151.

[10]陸俊, 朱炎平, 彭文昊, 等. 智能用電用戶行為分析特征優選策略[J]. 電力系統自動化, 2017, 41 (5): 58-63.

[11]馮曉蒲, 張鐵峰. 基于實際負荷曲線的電力用戶分類技術研究[J]. 電力科學與工程, 2010, 26 (9): 18-22.

[12]VIEGAS J L, VIEIRA S M, SOUSA J M C. Electricity demand profile prediction based on household characteristics [C]//European Energy Market. IEEE,2015:1-5.

[13]張素香, 劉建明, 趙丙鎮, 等. 基于云計算的居民用電行為分析模型研究[J]. 電網技術, 2013, 37 (6): 1542-1546.

[14]朱文俊, 王毅, 羅敏, 等. 面向海量用戶用電特性感知的分布式聚類算法[J]. 電力系統自動化, 2016, 40 (12): 21-27.

[15]張欣, 高衛國, 蘇運. 基于函數型數據分析和k-means算法的電力用戶分類(英文)[J]. 電網技術, 2015, 39 (11): 3153-3162.

[16]劉思, 李林芝, 吳浩, 等. 基于特性指標降維的日負荷曲線聚類分析[J]. 電網技術, 2016, 40 (3): 797-803.

[17]劉莉, 王剛, 翟登輝. k-means聚類算法在負荷曲線分類中的應用[J]. 電力系統保護與控制, 2011, 39 (23): 65-68.

[18]譚璐. 高維數據的降維理論及應用[D]. 北京:國防科學技術大學, 2005.

[19]謝娟英. 無監督學習方法及其應用[M]. 北京:電子工業出版社, 2016.