引導學生從整體的角度理解數(shù)學概念
——《認識小數(shù)》教學設(shè)計及解讀
朱國榮 王 揚
【教學內(nèi)容】
蘇教版三年級下冊第100頁。
【課前思考】
本課是學生第一次認識小數(shù),是對數(shù)系認識的一次重要擴展。它與整數(shù)相比,在意義、書寫形式、計數(shù)單位、計算法則等方面有某些相同的地方,但也有一定的差異。教材先安排認識整數(shù)部分是0的小數(shù),再認識整數(shù)部分不是0的小數(shù),最后介紹小數(shù)各部分的名稱。雖說是初步認識,但我們就僅僅停留于會認、會讀、會寫小數(shù)這些零碎的知識“點”嗎?我們知道,沒有正式學過小數(shù)的學生,在生活中或多或少對小數(shù)知識已有了一定的感性認知。面對這樣的情形,如果目光僅僅局限于這些知識點的認知,學生所獲得的也不過是些基礎(chǔ)性的知識,其豐厚的數(shù)學內(nèi)涵會大大縮水。我們可以更深入地思考,為什么要學習小數(shù)?它與分數(shù)、整數(shù)有什么聯(lián)系與區(qū)別?小數(shù)本身的特點與價值在哪里呢?
帶著這樣的思考,我們重新審視這節(jié)課的教學設(shè)計,對教材現(xiàn)有內(nèi)容進行取舍與改造,將本節(jié)課分為三個板塊:“分”,小數(shù)出現(xiàn)了;“合”,小數(shù)變大了;“分分合合”,小數(shù)變多了。這三個板塊,成為教者雕琢、展開的基點,避免浮于表面的知識點流程的教學。這些點在情境設(shè)置、師生交流、問題突破中逐漸豐滿成一個個板塊,板塊名稱從學生角度擬定,通俗易懂。
這三個教學環(huán)節(jié)層層遞進、自然流暢,呈現(xiàn)了知識發(fā)生、發(fā)展的過程,展現(xiàn)了一個豐富而完整的知識鏈條。與此同時,在教學的過程中,教師引導學生感悟了整體的思想,學會了從整體的角度去審視問題、分析問題、解決問題,從而使他們的思維得到了拓展,智慧得到了增長。
【教學過程】
板塊一:“分”,小數(shù)出現(xiàn)了。
1.整數(shù)→分數(shù)→小數(shù)。
師:(出示長方形)這是什么圖形?(出示直尺)長是多少?寬呢?
師:(出示另一個長方形)老師這兒還有一個長方形。你還能像剛才那樣一口報出它的準確長度嗎?
師:為什么不能?(因為長不足一分米)
師:借助我們以往的學習經(jīng)驗,不足1分米時,我們可以用什么辦法表示出它的準確長度呢?
生:用厘米作單位。
生:可以用分數(shù)來表示。
師:不管是用厘米作單位,還是用分數(shù)來表示,我們都是把這1分米怎樣?
師:(出示板塊標題“分”)怎么分?(把1分米平均分成10份)
師:為什么平均分成10份?(1分米等于10厘米)
師:長是多少?如果用分米作單位呢?可以用我們學過的哪個數(shù)來表示?寬呢?
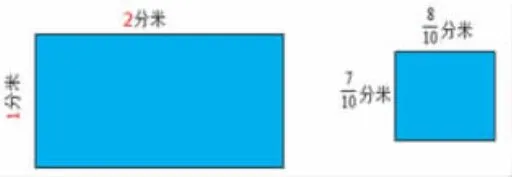
(1)比較:剛才我們測量了兩個長方形的長和寬,都是用分米作單位,為什么第一個長方形的長和寬可以用整數(shù)表示,而第二個長方形的長度卻要用分數(shù)來表示?
(2)小結(jié):當不足1分米的時候,我們就把1分米分一分,用分數(shù)來表示。除了分數(shù),還可以用新的數(shù)——小數(shù)來表示。
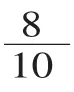
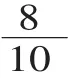
(繼續(xù)出示板塊名稱:,小數(shù)出現(xiàn)了)
師:今天我們就一起來認識小數(shù)。
【設(shè)計解讀:教學中只有引發(fā)心理沖突,讓學生在解決問題中感受到認知矛盾,才能體會小數(shù)出現(xiàn)的必然性。學生根據(jù)自己的經(jīng)驗會想到繼續(xù)更小地分,突出了關(guān)鍵詞“分”。學生發(fā)現(xiàn)在實際生活中還需要比單位1更小的計量。透過“分”,我們因需要而看到數(shù)的擴展、認知的遷移。】
2.小數(shù)的讀寫、意義。
(1)讀寫。
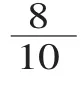
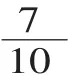
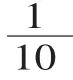
(2)意義。
師:0.4分米表示哪一個分數(shù)?你能畫圖表示出0.4分米嗎?
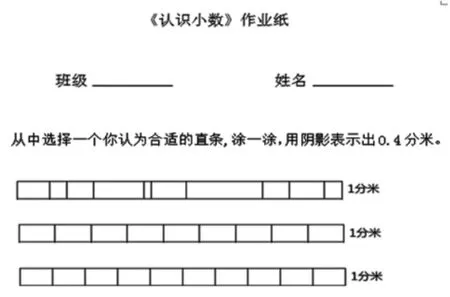
(學生上展臺反饋)
師:為什么不選圖一?(小數(shù)和分數(shù)一樣都必須建立在平均分的基礎(chǔ)上)
師:為什么不選圖二?(我們今天學習的小數(shù)都是把“1”平均分成了10份)
師:(PPT去除圖一圖二,保留正確的圖三)像這樣把1分米平均分成10份,1份是多少?(0.1分米)現(xiàn)在呢?十分之四分米,也就是0.4分米。
師:0.4分米是怎么來的?(把1分米平均分成10份,取其中的4份)
師:原來0.4和十分之四的意義是一樣的。誰再來說一說?0.4里有幾個0.1?
【設(shè)計解讀:本環(huán)節(jié)教者設(shè)計了3個別具匠心的直條圖,讓學生用已學過的分數(shù)知識,對3個直條圖的特征進行重新審視,從“平均分”到“平均分成10份”,學生在不知不覺中逐步建構(gòu),接近了0.4的本質(zhì),完善了認知體系。】
(3)分數(shù)與小數(shù)的聯(lián)系。
師:現(xiàn)在我們一起把剛剛用到的分數(shù)和小數(shù)整理在一起。

比較:仔細觀察,左邊的分數(shù)和右邊的小數(shù)有什么聯(lián)系?同桌討論一下。
師:你能再舉出一組這樣的例子嗎?
小結(jié):十分之幾就是零點幾,零點幾也可以寫成十分之幾。清楚道出了今天所學的小數(shù)和分數(shù)之間緊密的關(guān)系。帶著我們的發(fā)現(xiàn),玩?zhèn)€搶答游戲。
看圖說小數(shù)。
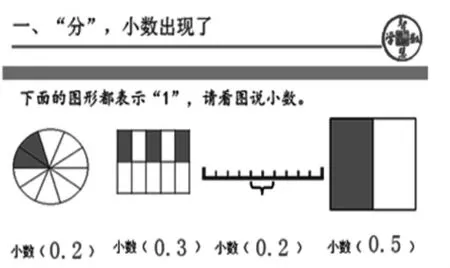
師:這幾幅圖分別用哪些小數(shù)表示呢?
師:圖1和圖3有些不一樣,為什么陰影部分都表示0.2?有什么相同點?
生:圖1是把一個圓看作“1”平均分成10份,圖3的”1”表示一條線段。
師:1還會是什么樣?(所有圖形)除了圖形,物體可不可以?比如蛋糕?
小結(jié):不管什么樣子的“1”,只要平均分成了10份,取出幾份就是零點幾。
師:最后一幅圖用哪個小數(shù)表示呢?為什么是0.5? 表示0.1的圖又是哪個?

【設(shè)計解讀:本環(huán)節(jié)教者精心創(chuàng)設(shè)了“看圖說小數(shù)”的游戲活動,將小數(shù)、分數(shù)知識有機地融為了一體。通過數(shù)形結(jié)合,學生在對圖形的比較、爭論中,慢慢逼近小數(shù)的本質(zhì),深刻感受到小數(shù)與分數(shù)間的聯(lián)系。】
板塊二:“合”,小數(shù)變大了。
師:0.8、0.2 都小于 1,小數(shù)都比1小嗎?
1.認識比1大的小數(shù)。
出示:

固體膠是多少元?你能試著用小數(shù)表示嗎?
師:2角為什么是0.2元?
小結(jié):1元和0.2元合起來就是1.2元。你看他在用一種新方法找到小數(shù)了。
師:(課件出示:合)他把整數(shù)1元和小數(shù)0.2元合起來得到一個新的小數(shù)1.2元。
師:1.2還比1小嗎?你能用畫圖表示出來嗎?
師:(出示1個正方形)如果這個正方形表示1元,用它能表示出1.2元嗎?夠嗎?(出示第2個正方形)你打算怎么涂色表示1.2,和你的同桌商量一下。
師:根據(jù)圖,誰再來說一說1.2是怎樣合成的? 現(xiàn)在變成了什么小數(shù)?(課件演示逐個增加一份,讓學生說出小數(shù):1.3、1.4、1.5、1.6……2,10個 0.1 又合成了1,加上前面的整數(shù)1,所以是2)
師:如何用涂色部分表示出2.1元呢?(圖形表示:整數(shù)2和小數(shù)0.1又合成一個小數(shù)2.1)
2.介紹小數(shù)各部分的名稱。
出示:

師:文具盒是多少元呢?怎么想的?
師:剛才我們合成了小數(shù)1.2和3.5,小數(shù)小數(shù),是不是都很小
啊?看一看。
出示:

師:2999元9角=2999.9元。它是小數(shù)嗎?它小嗎?一起來讀一讀。
師:它是怎么合成的呢?誰來說一說。(2999.9元是由2999元和0.9元合成的)
小結(jié):看來通過“合”,我們也可以得到一個比較大的小數(shù)。
師:這些小數(shù)中間都有個小圓點,我們把它叫做小數(shù)點,小數(shù)點左邊的部分叫做整數(shù)部分,小數(shù)點右邊的部分叫做小數(shù)部分。
小結(jié):整數(shù)與小數(shù)是相通的。合起來,小數(shù)變大了。
【設(shè)計解讀:小數(shù)和整數(shù)都符合“十進制記數(shù)法”的計算規(guī)則。分數(shù)和小數(shù)都是以平均分為基礎(chǔ)的,可以說整數(shù)、分數(shù)、小數(shù)之間有著千絲萬縷密不可分的聯(lián)系。第二板塊中突出關(guān)鍵詞“合”。教學中緊扣分數(shù)和小數(shù)對應(yīng)改寫,突出對小數(shù)意義的概括性理解。學生自主發(fā)現(xiàn),把整數(shù)和純小數(shù)“合”起來,小數(shù)有時也不小呀。在這個板塊,學生發(fā)現(xiàn)“合”也是一種新的表示小數(shù)的方法,通過“合”,從純小數(shù)到帶小數(shù),進一步豐富了學生對小數(shù)的認識,讓學生感受到數(shù)學的統(tǒng)一與和諧,逐步展現(xiàn)了一個全面而豐富的客觀世界,在這其中,學生開闊了視野,提升了認識,明辨了思想,生發(fā)了智慧。】
板塊三:“分分合合”,小數(shù)變多了。
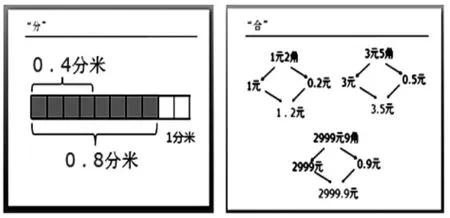
師:回憶一下,課一開始,我們怎樣選用直條來表示0.4分米?
生:把這個直條看作1分米,平均分成10份,其中的4份表示0.4分米,8份表示0.8分米,我們通過“分”得到了小數(shù)0.4、0.8。
師:1元2角我們又是怎么把它寫成小數(shù)的呢?
生:我們通過“合”的方式把1和0.2合起來就是小數(shù)1.2元。
小結(jié):通過分,我們得到了這些小數(shù);又通過合的方法,找到了這樣的小數(shù)。分分合合,小數(shù)變多了。
師:老師帶來一條神奇的直線。這些數(shù)是小數(shù)嗎?

師:像 1、2、3、4、5 等表示物體個數(shù)的數(shù)是自然數(shù),0也是自然數(shù)。它們都是整數(shù)。
師:在這條直線上,你看到了幾個數(shù)?直線上只有5個數(shù)嗎?
師:你能用數(shù)學的眼光找到小數(shù)嗎?比如0—1之間?

(先把0—1之間平均分成10份)
(學生上臺演示:找出0.1—0.9)
師:通過“分”,在 0-1 之間可有序地找到這么多的小數(shù),真棒!他找到的都比1小,誰能找的比1大的小數(shù)嗎?
師:怎樣可以快速找到2.9的位置。(2-3之間,接近3)100.9在哪兩個整數(shù)之間?
小結(jié):雖然屏幕上看不見,但我們想象可以推理出來,越往右數(shù)越來越大。
師:下面玩?zhèn)€猜數(shù)游戲。
這個數(shù)在3-4之間,可能是多少?(3.6)
師:這個數(shù)還在3-4之間,比3.6大,可能是多少?(3.7)
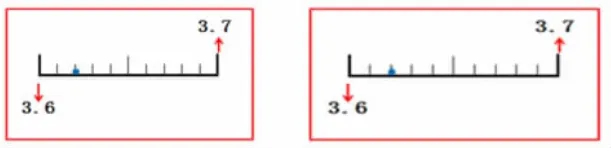
師:(出示一個點)這里是幾?這里能用3.6表示嗎?能用3.7表示嗎?
師:有什么辦法可以準確表示它的位置呢?
師:就要把3.6-3.7這段怎么辦?(再平均分成10份)
師:3.6-3.7這段平均分成10份,現(xiàn)在可以準確表示了嗎?在3.6和這個數(shù)之間還有小數(shù)嗎。還有很多很多呢。
小結(jié):像這樣,我們還可以繼續(xù)分下去,得到的計數(shù)單位越來越小,精確的程度也越來越高。整數(shù)、分數(shù)、小數(shù)都可以在這條直線上找到自己的位置,它們之間有著緊密的聯(lián)系。分分合合,有小有大,我們發(fā)現(xiàn)數(shù)越來越多,越來越密了。
【設(shè)計解讀:這個板塊中突出關(guān)鍵詞“分分合合”。從小數(shù)的產(chǎn)生,體驗數(shù)系的擴充過程;從小數(shù)這一特定的內(nèi)容,溝通整數(shù)、分數(shù)和小數(shù)之間的內(nèi)在聯(lián)系;從發(fā)現(xiàn)3.6和3.7之間的“空隙”使我們得到的計數(shù)單位越來越小,精確的程度也越來越高,小數(shù)使我們的計數(shù)更精確。“分”,小數(shù)出現(xiàn)了;“合”,小數(shù)變大了;“分分合合”,小數(shù)變多了。環(huán)環(huán)相扣,層層遞進。這一系列看似平常的學生活動,卻將知識脈絡(luò)清晰地鋪陳開來,引發(fā)學生自由思考、自覺起疑,促進學生思維向深度發(fā)展。從零散到完整,從朦朧走向清晰,從清晰走向深刻,展示了人類認識事物的過程,蘊含了數(shù)學學習中逐步提升的智慧。本課設(shè)計早已跳出了以往的教學模式,將問題開放化,有很大的包容性和可選擇性,讓人不由想起康托的話“數(shù)學的本質(zhì)是自由的”。】

