三角換元破解數學競賽題*

●　　(常熟市中學,江蘇 常熟　215500)

現行的《高中數學課程標準》已降低了對不等式的要求，且將不等式證明納為《數學(選修4-5)》中的理科內容，因此大部分學生在高中階段不能系統學習和掌握一些重要的不等式(如均值不等式、柯西不等式、排序不等式、伯努利不等式等)以及不等式證明的方法和技巧.一些數學學科優秀的學生，有志于參加高校的自主選拔和各類數學競賽考試，而這些考試中涉及不等式知識的試題較多且考查要求較高.那么如何來解決這個矛盾呢？考慮到三角函數是高中數學的基礎知識，也是高考重點考查的內容之一，學生普遍掌握得比較扎實.為此，筆者用全國高中數學聯賽各省市預賽題的三角解法為例，整理出一類以三角換元為手段，將競賽題轉化為三角函數問題來處理的解題模式，供讀者學習與參考.

1　正弦與余弦的換元

1.1正余弦換元

例1已知圓x2+y2=1與拋物線y=x2+h有公共點，求實數h的取值范圍.

(2011年全國高中數學聯賽江蘇省預賽試題)

h=y-x2=sinθ-cos2θ=

sin2θ+sinθ-1=

評注利用公式sin2θ+cos2θ=1進行正弦與余弦換元是最常用的一種三角換元手段.

例2實數x,y滿足x2+y2+xy=3，求x2+y2的取值范圍.

(2016年全國高中數學聯賽河北省高二預賽試題)

分析將已知條件配方，得

故x2+y2的取值范圍為[2,6].

評注通過配方進行正弦與余弦換元是一種比較有效的三角換元手段，這里配方是要領.需要指出的是利用不等式知識解題，一般只能解決一個方向.

本題用不等式來處理時，學生可能會這樣來解：

從而得到錯誤結果[2,+∞).當然用不等式來解答本題，只要運用得當，也能得出準確結論的.事實上，只要考慮另一個方向，再增加一個不等式即可.其正確解答過程為：一方面，

另一方面，

由此可知，利用不等式解題，靈活性較強，技巧性較高.另外應該指出，若改變條件或所求式子，例如：改求2x2+3y2的取值范圍，則借助不等式來解答的難度大大增加，沒經過不等式系統訓練的學生是難以完成的，而用上述三角換元手段可以同樣完成解答.

1.2單弦換元(正弦或余弦)

(2015年全國高中數學聯賽山西省預賽試題)

從而

ysinθ-cosθ=-2y，

于是

即

故

說明本題中用到了一個重要變換——“合一公式”：

(2013年全國高中數學聯賽安徽省預賽試題)

分析函數的定義域為[-2,2],可設x=2cosθ,其中θ∈[0,π]，則

y=|2cosθ+1|+|2cosθ-1|+2sinθ.

y=4cosθ+2sinθ=

y=-4cosθ-2sinθ=

評注根據正弦或余弦函數的值域,結合已知條件可進行正弦(或余弦)換元，將問題轉化為三角函數問題，再利用三角知識解決.利用單個正弦或余弦換元時,用正弦或余弦一般可以任選，但限制角的范圍必須滿足題設要求.

2　正余切與正余割的換元

2.1切割換元

(2017年全國高中數學聯賽四川省預賽試題)

從而

于是

|k|≥1，

即

|x-y|≥2,

評注利用sec2θ-tan2θ=1，可進行正切與正割的三角換元，可將競賽題轉化為三角問題.

2.2正切(余切)換元

(2014年全國高中數學聯賽內蒙古自治區預賽試題)

即

從而

于是

即

y2≥8,

2.3正割(余割)換元

(2013年全國高中數學聯賽湖北省預賽試題)

分析由于函數的定義域為(-∞,-1]∪[1,+∞)，因此可設

評注根據題目的結構特征，結合正切(余切)與正割(余割)的值域可以進行正切換元或正割換元.

3　引參后三角換元

例8已知x,y∈R，且2x2+3y2≤12，求|x+2y|的最大值.

(2017年全國高中數學聯賽河北省預賽試題)

分析令2x2+3y2=r2，則

0≤r2≤12.

例9若a，b，c∈R，a2+b2≤c≤1,求a+b+c的最大值和最小值.

(2013年全國高中數學聯賽江蘇省復賽試題)

a+b+c=r(cosθ+sinθ)+c=

評注對于條件式為不等式的問題，可以通過引入參數、三角換元，利用平方關系進行正余弦換元或切割換元.

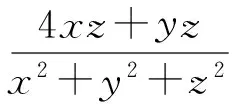
(2017年全國高中數學聯賽福建省預賽試題)

4　先構造再換元

4.1直接構造

(2016年全國高中數學聯賽新疆維吾爾自治區高一預賽試題)

評注根據條件x>0,y>0且x+2y=2，可將條件構造為二元二次問題，從而可利用三角換元的方法來解答.

4.2間接構造

(2016年全國高中數學聯賽新疆高一預賽試題)

u2=2-x，v2=3x+12,

得

3u2+v2=18.

評注通過整體換元，將原問題構造為可進行三角換元的問題，從而完成問題的解答.

綜上可知，“三角換元”是解決范圍(如最值、定義域、不等式)問題的一把利器，借助上述4種三角換元手段可實現代數(幾何)問題向三角函數問題的有效轉化.采用“三角換元”解題可規避應用不等式知識解題時靈活多變的方法和高難技巧，強化三角函數的應用意識；解題有明確的指向和固有的定式，思維流暢自然，使很多復雜的競賽題都能手到擒來，迎刃破解.

在本文中，筆者所選取的均是競賽試題，事實上，對高考試題的解答，三角換元法也具有廣泛的適用性.三角換元法解題既適應新課改的需求，又符合“淡化特殊技巧，注重通性通法”的新高考理念，且能有效訓練和提高學生的思維能力與洞察能力，促進數學的高效學習，值得我們進行深入研究并熟練掌握.