體驗數(shù)學(xué)概念教學(xué)的生成過程*
——基于“指數(shù)函數(shù)及其性質(zhì)”概念教學(xué)的反思與認識

●　　　　(杭州高級中學(xué),浙江 杭州　321008)

最近在浙江省杭州市優(yōu)質(zhì)課評比中，筆者開設(shè)了一堂公開課“指數(shù)函數(shù)及其性質(zhì)”.下面將筆者的想法、教學(xué)過程和反思分享給大家，供參考.

1　情景引入

情景1對折一張足夠大的紙，對折一次，厚度變成原來的2倍，對折兩次，厚度變成原來的4倍，對折3次，厚度變成原來的8倍，……，如果對折x次，厚度變成原來的y倍，如何描述這兩個變量之間的關(guān)系？如果紙張的厚度為0.1 mm，對折30次，總厚度為多少？對折50次呢？

生1:y=2x(其中x∈N*).

師：我們檢驗一下，對任意x∈N*,是否都有唯一確定的y與之對應(yīng).

生(全體)：是.

師：我們把x與y的對應(yīng)關(guān)系叫做函數(shù)關(guān)系，x是自變量，y是函數(shù)值,定義域為N*.接下來，我們看第二個問題：對折30次，總厚度為多少？

生2：y=0.000 1×230=107 374.182 4 (m).

師：107 374.182 4>8 844.34.如果能折30次，那么紙的厚度將超過珠穆朗瑪峰的高度，那折50次呢？

視頻播放資料根據(jù)科學(xué)愛好者的說法：

對折3次=你指甲的厚度;

對折7次=128頁的筆記本的厚度;

對折10次=一只手的寬度;

對折23次=1公里，大約3 280步;

……

對折30次=100公里,這樣的厚度已經(jīng)足夠帶你上天了;

對折42次=這樣的厚度可以到達月球；

對折51次=這樣的厚度可以拜訪太陽；

對折81次=127 786光年，大概就是一個仙女座星系；

對折103次=930億光年，大于已知宇宙的厚度.

師：這出乎我們的意料，令人震撼.因為x越大，函數(shù)值上升的速度越快，我們將這種上升速度，形象地稱為“指數(shù)爆炸”.

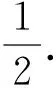
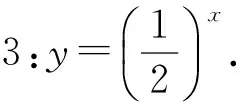
師：很好，還有其他想法嗎？

生4：其中x∈N*.

師：x是正整數(shù)嗎？請問時間有沒有1.5年、1.25年的說法？

生(全體):有.

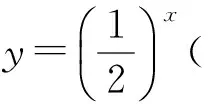
教學(xué)反思情景引入讓學(xué)生體會數(shù)學(xué)來源于生活，大量的數(shù)學(xué)模型都是以生活實例為現(xiàn)實原形的.

本環(huán)節(jié)中有2個亮點：

1)情景1中的一段素材資料(教學(xué)時是一段視頻)，深深地吸引了學(xué)生，喚起了學(xué)生的學(xué)習(xí)熱情和強烈的求知欲.

2)在設(shè)計上，情景1和情景2層層遞進，定義域從N*到全體正數(shù)，將兩個函數(shù)抽離實際背景，巧妙地把兩個函數(shù)的定義域推廣到R,起到了承上啟下的作用.

2　概念建構(gòu)

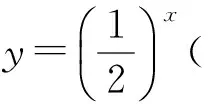
生5：都是指數(shù)冪形式.

生6：底數(shù)都是常數(shù).

生7：自變量都在指數(shù)位置.

生8：定義域都為R.

師：很好!1)都是指數(shù)冪形式;2)自變量在指數(shù)位置;3)底數(shù)是常數(shù);4)定義域為R.類似這樣的函數(shù)，還能再舉幾個例子嗎？

生9：y=6x,y=(0.6)x.

師：綜合這些函數(shù)的共同點，能用一個統(tǒng)一的形式來表示嗎?

生10：y=ax.

師：這是一般的函數(shù)模型，其中x是自變量，y是函數(shù)值，底數(shù)a不同就得到不同的函數(shù).那么，若要滿足x∈R，底數(shù)a的取值有什么要求呢？

生11：a≠1.

師：為什么？

生12：因為當(dāng)a=1時,y=1是常數(shù)函數(shù)，不具備單調(diào)性.

師：還有什么要求呢？

生14：a≠0，因為00沒有意義.

師：大家分析得非常好.我們得到a的取值范圍a>0且a≠1，此時，y=ax的定義域為R.

(教師PPT投影指數(shù)函數(shù)的概念:一般地，函數(shù)y=ax(其中a>0且a≠1)叫做指數(shù)函數(shù)，其中x是自變量，定義域為R.)

例1判斷下列函數(shù)中哪些是指數(shù)函數(shù)？

1)y=(-2)x；2)y=2x+1；3)y=3·4x；

4)y=x4；5)y=0.3x；6)y=2x+1；

7)y=πx；8)y=xx.

教學(xué)反思概念建構(gòu)就是告訴學(xué)生要從實際例子中抽象概括出指數(shù)函數(shù)模型，啟發(fā)學(xué)生運用函數(shù)模型表述、思考和解決現(xiàn)實世界中蘊含的規(guī)律[1].

本環(huán)節(jié)中有2個亮點：

1)讓學(xué)生歸納出一些具體函數(shù)的共同特征，再讓學(xué)生舉出一些類似函數(shù)，最后進行歸納概括得一般形式.讓學(xué)生經(jīng)歷由部分到整體、由個別到一般的歸納推理過程.

2)學(xué)生能輕松自然地得到a>0且a≠1，得益于教師在情景引入中巧妙地將指數(shù)函數(shù)的定義域變成R..

3　性質(zhì)探究

師：到此我們得到了一個新的函數(shù)模型，那么按照基本初等函數(shù)的研究思路，接下來我們要研究函數(shù)的什么性質(zhì)呢？

生15：單調(diào)性、最大值、最小值、奇偶性等.

師：對，很好！這些就是我們要研究的函數(shù)性質(zhì)，而我們通常根據(jù)什么載體去研究函數(shù)的性質(zhì)呢？

生16：函數(shù)圖像.

師：很好，畫函數(shù)圖像可用什么方法?

生17：描點法.

師：描點法的具體步驟是什么？

生18：列表、描點、連線.

師：研究基本初等函數(shù)性質(zhì)的基本方法和步驟:形成函數(shù)定義→作出函數(shù)圖像→研究函數(shù)性質(zhì)→運用函數(shù)性質(zhì).

師：接下來我們用描點法畫出指數(shù)函數(shù)的圖像，但是畫哪一個呢？畫y=ax嗎？

生19：y=ax的圖像一下子畫不出來，但可以畫y=2x.

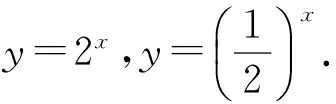
(學(xué)生開始動手列表畫圖，教師巡邏，然后將其中一位學(xué)生的作圖情況進行投影，并在此強調(diào)畫圖需要列表、描點、連線等步驟.教師打開幾何畫板，直接演示畫圖，讓學(xué)生直接面對面感受數(shù)形結(jié)合之美.)

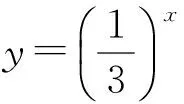
(學(xué)生畫好后，教師再對學(xué)生所畫的圖像作出評價.)

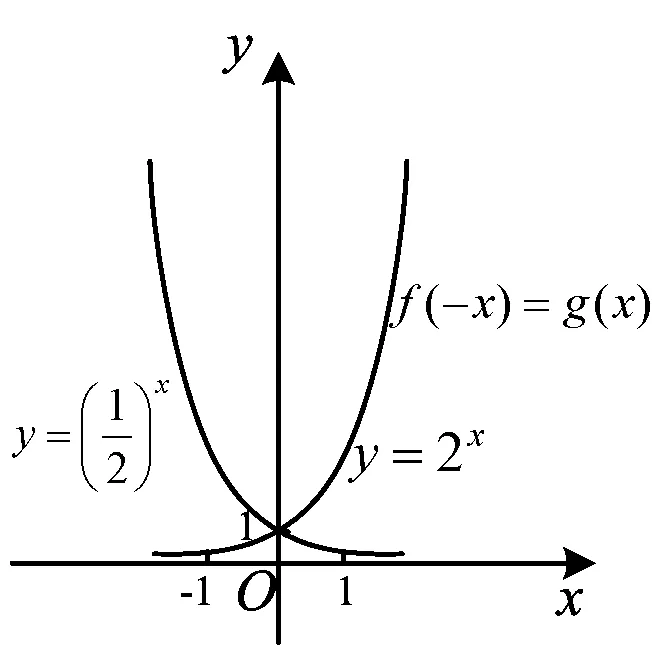
圖2

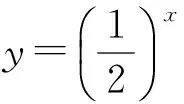
(教師用PPT演示，讓學(xué)生感受列表、描點、連線的過程.)

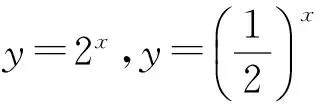
生20：這兩個函數(shù)圖像關(guān)于y軸對稱.

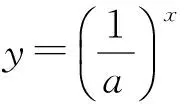
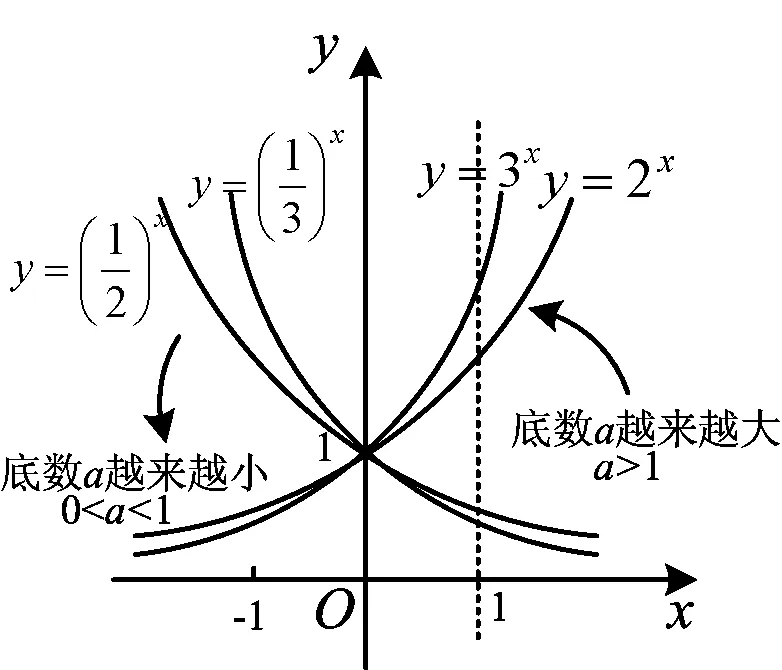
圖2

生21：如圖2，可以按照底數(shù)a分成兩類：1)當(dāng)a>1時，y=ax單調(diào)遞增；2)當(dāng)0

生22：它們的共同點是過點(0,1)，并且始終在x軸上方.

生23：當(dāng)a>1時，a越大，圖像越靠近y軸；當(dāng)0

師：把這些圖像特征分別對應(yīng)相應(yīng)的函數(shù)性質(zhì)，我們一起把函數(shù)性質(zhì)表格填完(填表過程略).

教學(xué)反思1)教師雖然畫出圖像，并用函數(shù)圖像來研究函數(shù)性質(zhì)，但是因為設(shè)計的問題比較分散、零碎、封閉，沒有形成問題串的形式，所以沒能讓學(xué)生從一個基礎(chǔ)問題出發(fā)層層遞進并展開討論,教師上課過程就顯得比較凌亂.如果把問題變成：請大家自己選擇a的值，畫幾個具體函數(shù)的圖像，然后分小組討論圖像有什么特征.用這樣一個問題引領(lǐng)，顯得開放，既有學(xué)生的獨立思考，又有小組合作學(xué)習(xí)，從整體上把握函數(shù)研究的一般方法[2].

2)這一環(huán)節(jié)可以很好地體現(xiàn)“從具體問題出發(fā)→觀察、分析→歸納、類比→提出猜想→演繹證明”這個數(shù)學(xué)發(fā)現(xiàn)的一般過程.雖然教師努力想體現(xiàn)“從具體到抽象、從特殊到一般的歸納推理形式”，但僅由幾個特殊函數(shù)圖像得到函數(shù)性質(zhì)，沒有大量用幾何畫板演示當(dāng)a在(1,+∞)和(0,1)兩個范圍內(nèi)變化時的圖像變化的一般情況及函數(shù)性質(zhì)，不利于學(xué)生形成從特殊到一般的歸納推理模式[3].

3)推理與證明是本節(jié)課需要重視的一個問題，這正是數(shù)學(xué)有別于其他學(xué)科的顯著特點，數(shù)學(xué)結(jié)論的正確性必須通過邏輯推理的形式加以證明.但本環(huán)節(jié)僅由幾個具體函數(shù)的圖像歸納出相關(guān)結(jié)論，并未對結(jié)論給出證明或者說明.

4　鞏固應(yīng)用

鞏固應(yīng)用就是內(nèi)化新知，深化對指數(shù)函數(shù)的理解，極大地提高了學(xué)生靈活運用圖像和性質(zhì)的能力.

師：指數(shù)函數(shù)及其性質(zhì)可以應(yīng)用在哪里呢？

圖3

例2已知指數(shù)函數(shù)f(x)=ax(其中a>0,且a≠1)的圖像經(jīng)過點(3,π)，求f(0)，f(1)，f(2).

(教師投影一位學(xué)生的解題情況，并在此強調(diào)解題的規(guī)范.)

師：由題意得f(1)=a，說明函數(shù)y=ax圖像也經(jīng)過點(1,a)，這不僅可以幫我們結(jié)合(0,1)簡單畫出指數(shù)函數(shù)y=ax的圖像，還可以解釋a越大，圖像越向上升(如圖3).

例3比較下列各題中兩個值的大小：

1) 1.72.5與1.73；2) 0.8-0.1與0.8-0.2；

(教師投影一位學(xué)生的解題情況，并在此強調(diào)解題歸納和總結(jié).)

師：總結(jié)比較大小的方法:1)當(dāng)?shù)讛?shù)相同且明確底數(shù)a與1的大小關(guān)系時，直接用函數(shù)的單調(diào)性來解；2)當(dāng)?shù)讛?shù)相同但不明確底數(shù)a與1的大小關(guān)系時，要分情況討論;3)當(dāng)?shù)讛?shù)不同時，可以轉(zhuǎn)化成同底數(shù)或借助中間值來比較兩個數(shù)的大小.

例4解下列關(guān)于x的不等式：

1)3x≥30.5；2)0.2x<25；3)ax2-2x≥a3.

這是挑戰(zhàn)題，對學(xué)生來說有點難度，教師可從思想、方法上加以提升和總結(jié).

教學(xué)反思本課是指數(shù)函數(shù)第一課，教學(xué)重點應(yīng)在指數(shù)函數(shù)模型的建構(gòu)及其性質(zhì)探究，不宜花過多時間用于例題講解，例題不能選得太難，不可以把概念課上成習(xí)題課.

5　歸納小結(jié)

師：本節(jié)課我們從知識點、數(shù)學(xué)思想、數(shù)學(xué)方法等方面學(xué)會了什么?

教學(xué)反思教師能夠從知識、思想方法層面加以小結(jié)，非常好，但最好加上學(xué)生的情感體驗，如:你體驗到了什么,感悟到了什么,等.

以上是筆者參加這次優(yōu)質(zhì)課比賽的一點感悟，在上課時筆者也注意到需對學(xué)生的回答及時肯定，以及規(guī)范自己的板書.重新回顧教學(xué)過程，并及時查找教科書及教學(xué)參考書，對概念課有了更深層次的理解，以下是筆者對概念課教學(xué)的一點體會：

1)結(jié)合一節(jié)課的重點和難點，以及教師對教材的分析，設(shè)計問題串，用問題驅(qū)動教學(xué)，將教師的三維目標(biāo)融入教學(xué)過程中.

2)仔細推敲數(shù)學(xué)概念中每個字的含義，如指數(shù)函數(shù)的定義域為R，為什么底數(shù)a有a>0且a≠1的要求.通過對概念的探索，加強學(xué)生對概念的理解和記憶.

3)《新課程標(biāo)準(zhǔn)》強調(diào)學(xué)生對知識的探求和發(fā)現(xiàn)的過程，不再像傳統(tǒng)教學(xué)那樣注重教師的教，因此教師要教會學(xué)生發(fā)現(xiàn)新知的方法.在教學(xué)過程中，教師設(shè)計生活情景，用一些具體函數(shù)的圖像特征和性質(zhì)歸納推理出一般結(jié)論，最后證明這些結(jié)論.讓學(xué)生在探索中尋找樂趣，學(xué)會用數(shù)學(xué)方法解決實際問題.

5)一定要注意數(shù)學(xué)符號的正確使用與轉(zhuǎn)化.概念的文字?jǐn)⑹觥⒎柋硎尽D形表示要轉(zhuǎn)化到位，如本節(jié)課中先是概括出指數(shù)函數(shù)的文字概念，進一步形成符號表示y=ax(其中x∈R)，最后畫出圖像進行性質(zhì)研究.

概念課的重要功能就是可以讓學(xué)生學(xué)會從數(shù)學(xué)角度看生活中的各種問題，培養(yǎng)學(xué)生的數(shù)學(xué)思想，并用數(shù)學(xué)知識解決生活中的實際問題，體現(xiàn)數(shù)學(xué)的生活美及抽象美[4].

[1]馬茂年.快樂教學(xué)改善心育領(lǐng)悟本

質(zhì)——從“教書匠”走向“名教師”[J].中學(xué)教研(數(shù)學(xué))，2013(7)：4-7.

[2]周仕榮．?dāng)?shù)學(xué)課堂規(guī)范的討論和分析[J]．?dāng)?shù)學(xué)教育學(xué)報，2012，21(1):80-81．

[3]王光明,刁穎.高效數(shù)學(xué)學(xué)習(xí)的心理特征研究[J]．?dāng)?shù)學(xué)教育學(xué)報，2009，18(5)：51-56.

[4]馬茂年，俞昕.課堂教學(xué)回歸“數(shù)學(xué)化”的討論和分析——以高中“數(shù)學(xué)歸納法”的教學(xué)為例[J].數(shù)學(xué)教育學(xué)報，2013，22(6)：83-84.