活躍在不等式證明中的調整法*

●　　(宏實中學，安徽 樅陽　246700)

1　試題呈現與解法探究

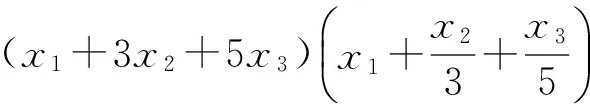
這是2017年全國高中數學聯賽一試第10題.從公布的參考答案來看，求最小值的方法比較常規，主要是柯西不等式的應用；求最大值的方法比較靈活，技巧性較強，解題的關鍵在于相關參數的配湊.在教學中，筆者得到另外一種解題方法.因為

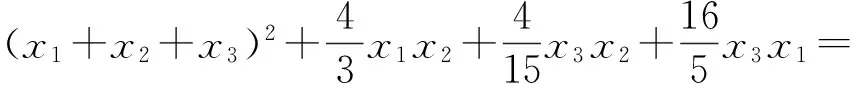
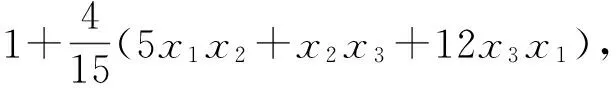
所以原問題可轉化為下面的例2：

例2設x1,x2,x3是非負實數，滿足x1+x2+x3=1，求P=5x1x2+x2x3+12x3x1的最大值和最小值.

解設x1,x2,x3是非負實數，P=5x1x2+x2x3+12x3x1的最小值顯然為0，當且僅當x1,x2,x3中有兩個值為0、一個值為1時，等號成立.問題的關鍵在于求P的最大值.

P=5x1x2+x2x3+12x3x1=

x1x2+x2x3+4x1x2+12x3x1=

(x1+x3)x2+x1(4x2+12x3)=

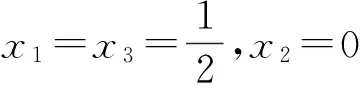
這是一種什么解題方法？解題方法的依據是什么？還有沒有其他的變形？事實上這是不等式證明中經常使用的調整法[1].在本題中，首先給出第一步調整“固定x2，使x1+x3為定值”，再給出第二步調整“讓x2在區間[0,1]上變動”，從而求出最大值.

2　什么是調整法

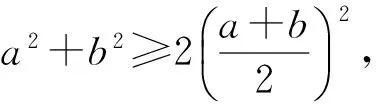
例4設a1≤a2≤a3≤…≤an,b1≤b2≤b3≤…≤bn為兩組實數，c1,c2,c3,…,cn是b1,b2,b3,…,bn的任一排列，則

分析這是人教A版《數學(4-5)》“不等式選講”中的一個著名的例子.它的證明比較簡單，主要運用了逐步調整法.注意到不等式A≥a,B≥b,(A-a)(B-b)≥0?AB+ab≥Ab+Ba，它表明：對于任意兩組數A,B;a,b,且A≥a,B≥b，總有AB+ab≥Ab+Ba.

也可以將它們調整到最小值

3　調整法的應用

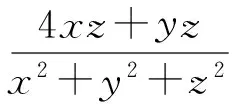
(2016年全國高中數學聯賽福建省預賽試題第10題)

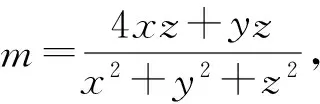
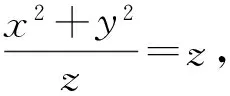
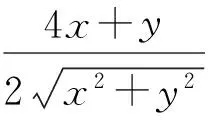
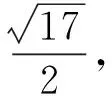
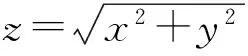
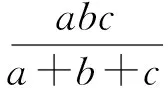
(2017年全國高中數學聯賽陜西省預賽試題第11題)

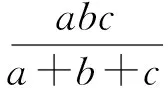
所以

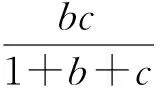
所以

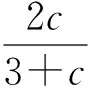
所以

g(c)min=g(3)=1，

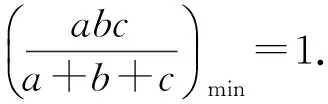
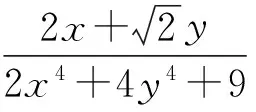
(2017年全國高中數學聯賽江蘇省復賽試題第5題)

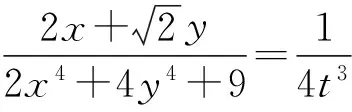
(1)

固定式(1)中的y，把x當作變量，構造函數

則

f′(x)=8x3-8t3,

(2)

由題意，函數f(x)有零點，即f(x)min≤0.

在式(2)中，把y當作變量，構造函數

由f(x)min≤0，知函數g(y)有零點，則

由題設t>0，從而t≥1，于是

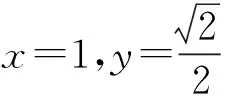
數學的本質就是用數學的眼光認識世界，揭示數學規律，總結數學方法，形成數學思想.在平時的解題過程中，師生要重視對問題和方法的追溯，刨根問底，追本求源，挖掘試題的數學本質，從中提煉出數學解題方法，這樣才能知其然，更知其所以然[3].

[1]羅增儒.數學解題學引論[M].西安：陜西師范大學出版社，2008.

[2]波利亞.怎樣解題[M].涂泓，馮承天，譯．上海：上海教育出版社，2001.

[3]葉會新.提高探究實效培養思維能力[J].中學教研(數學)，2017(6)：41-44．