淺談一類旋轉問題*

●　　(龍港高級中學,浙江 蒼南　325802)

1　試題再現，引發思考

例1如圖1，在正方形ABCD中，點E,F分別為邊BC,AD的中點，將△ABF沿BF所在直線進行翻折，將△CDE沿DE所在直線進行翻折，在翻折的過程中

()

A.點A與點C在某一位置可能重合

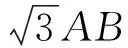
C.直線AB與直線CD可能垂直

D.直線AF與直線CE可能垂直

(2016年浙江省寧波市一模數學試題第10題)

按照筆者所任教班級學生的水平，此題的難度應該不是很大，而實際情況是4個選項出現的幾率差不多，這說明了學生在做這道題時，很多是猜的.那么問題出在哪里呢，問題的突破點又在哪里呢？

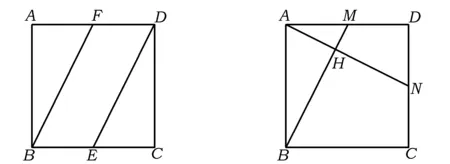
圖1　　　圖2

2　本源探索，形成結論

例1的本質是一個旋轉問題，可以歸納如下：

如圖2，已知正方形ABCD，M為邊AD的中點，△ABM繞BM旋轉，在翻折過程中：

問題1點A的軌跡是什么？

問題2點A在面BCDM內的射影所在曲線的軌跡是什么？

分析過點A作AH⊥BM，垂足為H，交直線CD于點N.在翻折的過程中，始終有BM⊥AH，BM⊥HN，即BM⊥面AHM.因此問題1的結論為：以H為圓心、AH為半徑的圓.問題2的結論為：直線HN.

我們把直線BM定義為旋轉軸，AH定義為軸垂線，平面AHM定義為軸垂面，則有如下結論及其推論：

結論1點A的軌跡為以垂足H為圓心、垂線段AH為半徑的圓；點A在面BCDM內的射影所在曲線的軌跡是直線HN.

推論1在翻折的過程中，點A在面BCDM內的射影為O，則點O必在軸垂線HN上.

推論2記點A在旋轉軸BM和面BCDM上的射影分別為H,O，則點A,H,O在展開圖中必定共線，且在軸垂線上.

3　變式拓展，變形應用

3.1點在棱上的射影

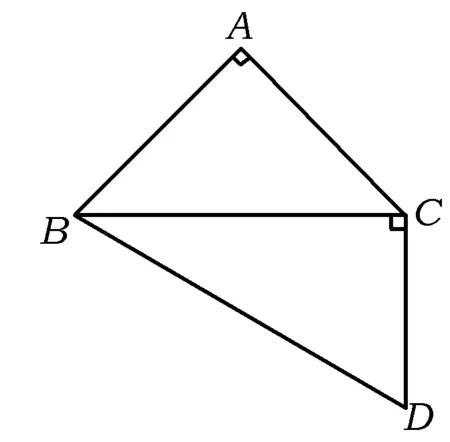
圖3

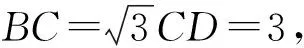
(2016年浙江省杭州市一模數學試題第13題)

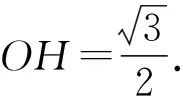
于是

得

此題的難點不在于計算，而在于如何找出題目中涉及到的相關點的位置，即動點的軌跡.若能準確無誤地找到，則能輕松地解決問題.

3.2點在面上的射影必在軸垂線上

例3如圖4，在長方形ABCD中，AB=2，BC=1,E為DC的中點，F為線段EC(端點除外)上一動點.現將△AFD沿AF折起，使平面ABD⊥平面ABC.在平面ABD內過點D作DK⊥AB，K為垂足.設AK=t，則t的取值范圍是______.

(2009年浙江省數學高考理科試題第17題)

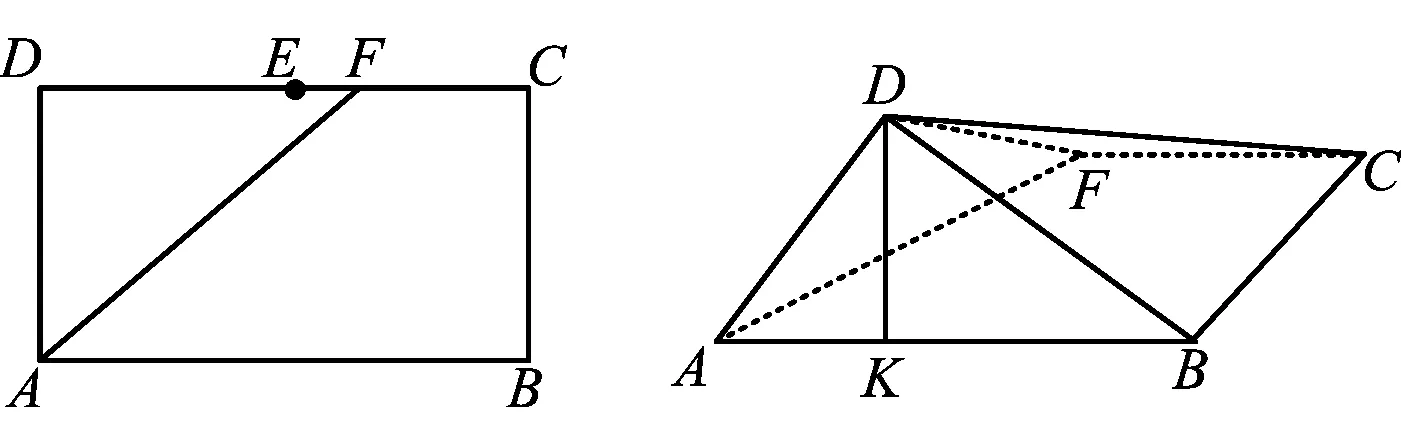
圖4　　　圖5

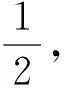
3.3三點必定共線，且在軸垂線上

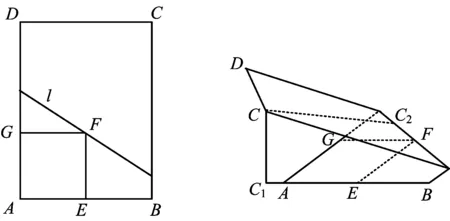
圖6　　　圖7

()

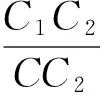
(2017年浙江省臺州市一模數學試題第10題)

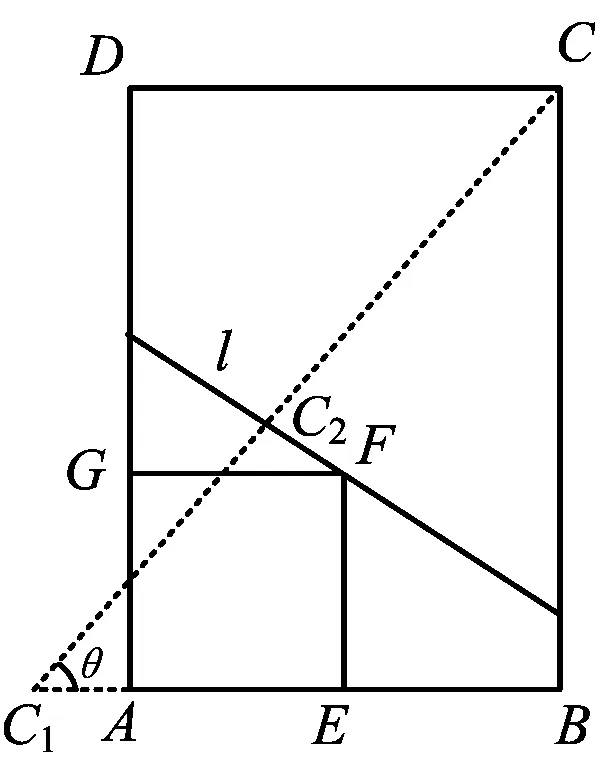
圖8

分析本題的條件比較復雜，難度較大，其本質是一個旋轉問題.利用推論2知點C,C2,C1共線，且與旋轉軸l垂直.過點C作l的垂線，垂足為C2，與AB的交點則為C1(如圖8).

設∠CC1B=θ，則

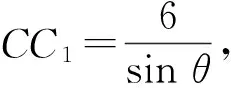
CC2=4sinθ+2cosθ,

本題最大的難度在于：如何化立體為平面，把空間的問題轉化為平面的問題.若知道如上結論和兩個推論，則能很容易想到作輔助線的方法，從而輕松地解決問題.

4　歸納總結，思想提升

實際上，任何一個旋轉問題都有旋轉軸、軸垂線、垂足和軸垂線與面內的線的交點，以及在旋轉過程中形成的軸垂面等問題，我們總能得到垂足和交點都是在一條直線上，即在軸垂線上，還有軸垂面與旋轉軸始終是垂直關系，進而得到旋轉點在已知面內的射影總在軸垂線上.若能很好地抓住這幾個關系，則能使問題簡單化、明朗化、本質化.