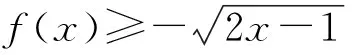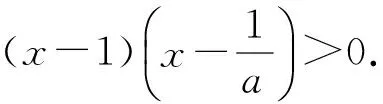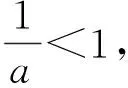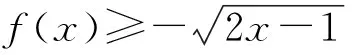例談“不等式恒成立問題”的幾種優化處理方式*
● (阜陽市第三中學,安徽 阜陽 236000)
“不等式恒成立問題”是高中數學中一個非常重要的問題,受到高考命題者的青睞,在試題中高頻考查.究其原因,主要是在探求這類問題的解題途徑時,通常需要運用函數、方程、不等式等中學數學核心知識以及數形結合、分類討論、轉化化歸等基本數學思想,其綜合性和靈活性都較強.筆者經過探究發現,若能在利用常見方法解決“不等式恒成立問題”的基礎上,結合一些優化處理,則可以使問題解決變得更簡潔、自然.下文為筆者探究的一點心得體會,與同行們交流,不當之處,敬請批評指正.
1 尋找不等式恒成立的必要條件進行優化[1]
不等式恒成立問題常見的形式為:如果對任意x∈I,都有f(x)≥0(或f(x)≤0),那么若x0∈I,則一定有f(x0)≥0(或f(x0)≤0).通過這個必要條件縮小了所含參數的范圍,優化了解題過程.現舉例一則,加以說明.
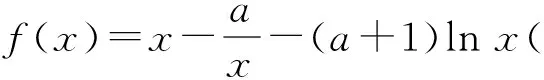
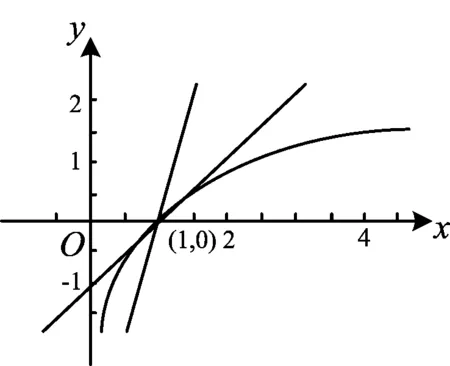
1)當0 2)是否存在實數a,使f(x)≤x恒成立?若存在,求實數a的取值范圍;若不存在,說明理由. 1)略. 2)解法1f(x)≤x恒成立可轉化為a+(a+1)xlnx≥0恒成立.令 φ(x)=a+(a+1)xlnx, 解法2f(x)≤x恒成立可轉化為a+(a+1)xlnx≥0恒成立,則 (a+1)xlnx≥-a. 因為a+(a+1)xlnx≥0對任意x∈(0,+∞)恒成立,所以x=1滿足上述不等式,即a≥0,從而 (a+1)xlnx≥-a, 于是 通過以上兩種解法不難發現:在題目沒有明確給出參數a的范圍時,只能先認為a∈R,這樣就要運用分類討論的思想.因為恒成立的不等式對所給變量范圍內的任意一個數都滿足,所以可先利用一些特殊值去縮小參數a的范圍,即尋找其成立的一個必要條件,從而在求函數最值時不需要或者減少分類討論的情況. 練習1設函數f(x)=a2lnx-x2+ax,其中a>0. 1)求f(x)的單調區間; 2)求所有實數a,使e-1≤f(x)≤e2對x∈[1,e]恒成立. (2011年浙江省數學高考文科試題第21題) 練習2設函數f(x)=(x-a)2lnx,其中a∈R. 1)若x=e為y=f(x)的極值點,求實數a; 2)求實數a的取值范圍,使得對任意的x∈(0,3e],恒有f(x)≤4e2成立. (2011年浙江省數學高考理科試題第22題) 定理1可推廣到x→a-0,x→a及x→∞的情形. 定理2也適用于x→a-0,x→a及x→∞的情形. 例2設函數f(x)=ex-1-x-ax2. 1)若a=0,求f(x)的單調區間; 2)當x≥0時,f(x)≥0,求實數a的取值范圍. (2010年全國數學高考新課標卷Ⅰ理科試題第21題) 1)略. 2)解由f(x)≥0得 ex-1-x-ax2≥0. 記h(x)=(x-2)ex+x+2,則 h′(x)=ex(x-1)+1. 設φ(x)=ex(x-1)+1,則φ′(x)=xex,因為x∈(0,+∞),所以φ′(x)>0,即φ(x)在x∈(0,+∞)上單調遞增,從而φ(x)>0,于是h(x)在x∈(0,+∞)上單調遞增,故h(x)>0,即g′(x)>0,進而g(x)在x∈(0,+∞)上單調遞增.此時可以發現函數g(x)在x=0處沒有意義,而 由洛必達法則知 即 由于學生在處理不等式恒成立問題時更青睞于選擇分離參數,構造一個不含有參數的函數,從而避免在求函數最值時的分類討論,但是經常會遇到這樣的問題:所構造的函數在定義域內是單調的,但是函數在定義域端點處沒有意義,此時需要借助洛必達法則進行優化處理. 1)求a,b的值; (2011年全國數學高考新課標卷Ⅰ理科試題第21題) 練習4設函數f(x)=x(ex-1)-ax2. 2)當x≥0時,f(x)≥0,求實數a的取值范圍. (2010年全國數學高考新課標卷Ⅰ文科試題第21題) 推論1若f′(a)>0,則存在δ>0,對任意x∈(a,a+δ)(或任意x∈(a-δ,a)),都有f(a) 推論2若f′(a)<0,則存在δ>0,對任意x∈(a,a+δ)(或任意x∈(a-δ,a)),都有f(x) 證明過程同推論1. 2)若f(x)≥g(x)恒成立,求實數a的取值范圍. (2013年遼寧省數學高考理科試題第21題) 1)略. 2)解令 其中x∈[0,1],則F(0)=0.由推論2知:若F′(0)<0,則存在δ>0,對任意x∈(0,δ),都有F(x) 所以 a≤-3, h′(x)=-x+2sinx, 記φ(x)=-x+2sinx,則 φ′(x)=-1+2cosx. 當x∈(0,1)時,φ′(x)>0,從而φ(x)在x∈[0,1]上單調遞增,進而 φ(x)≥φ(0)=0, 即當x∈(0,1)時,h′(x)>0,于是h(x)在x∈[0,1]上單調遞增,即 h(x)≥h(0)=0, 亦即 G(x)≥xh(x)≥0, 故實數a的取值范圍為(-∞,-3]. 此題的難度較大,得分率很低,學生解決“不等式恒成立問題”主要有以下兩種方法: 1)先采取分離參數的方法,將不等式轉化為 然后構造函數 其中x∈(0,1],從而轉化為求函數h(x)的最小值. 2)直接構造函數 其中x∈[0,1],從而把問題轉化為F(x)≥0恒成立,即求函數F(x)的最小值問題. 上述兩種解法由于所構造的函數形式過于復雜,直接求其最值的難度很大,因此難以順利解決問題,例3的參考答案利用多次分類討論、放縮以及構造函數,從學生層面上說,很難想到.若利用函數極限的局部保號性定理,可以縮小參數a的取值范圍(很多情況下已是所求答案),再通過構造函數就可以順利解決問題,起到了很好的優化作用. 筆者發現在各省市高考題中經常出現類似的不等式恒成立問題:“對任意x∈I,都有f(x)≥0(或f(x)≤0),并且區間I的某個端點x0滿足f(x0)=0,求所含參數的取值范圍”,這類問題都可以利用函數極限的局部保號性定理,使解決過程變得更自然. 例4設函數f(x)=ax+cosx,其中x∈[0,π]. 1)討論f(x)的單調性; 2)設f(x)≤1+sinx,求a的取值范圍. (2012年全國數學高考大綱卷理科試題第21題) 1)略. 2)解令g(x)=ax+cosx-1-sinx,其中x∈[0,π],則g(0)=0.由推論1知:若g′(0)>0,則存在δ>0,對任意x∈(0,δ),都有g(x)>g(0)=0,不符合題意,故g′(0)≤0.因為 其中x∈[0,π],所以a≤1. 上述解法利用函數極限的局部保號性定理縮小了參數a的取值范圍,把“a>-1”縮小為“-1 (2013年遼寧省數學高考文科試題第21題) 1)求曲線y=f(x)在點(0,f(0))處的切線方程; (2015年北京市數學高考理科試題第18題) 不等式恒成立問題常通過構造函數再求其最值解決,難點是所構造的函數形式過于復雜,在處理過程中需要多次運用分類討論和轉化與化歸的數學思想.基于這個難點,筆者通過以上3種優化“不等式恒成立問題”的處理方式,使解題過程變得更簡潔、自然,也更符合學生的認知水平. [1]夏炳文.縮小參數范圍優化“恒成立問題”的處理[J].中學數學研究,2016(4):38-40. [2]歐陽光中,朱學炎,金福臨,等.數學分析(上冊)[M].3版.北京:高等教育出版社,2007. 1.2恰當分類依據 1.2.1依據邏輯關系進行分類 必須要知道是依據什么,才能進行恰當分類. 1)根據數學的定義、性質、運算步驟、定理和公式進行分類討論,如負數定義、集合的含義和表示、函數的定義域和函數的單調性、0的任何次冪都是0、負數和0沒有對數、方程的兩邊同乘或除以同一個數方程仍然成立. 2)根據平面幾何圖形中點、線、面位置的不確定進行分類討論;根據不同情況下參數的不同進行分類討論,有些問題中存在參數,但是情況不同參數會發生變化,參數所代表的數值不同結果也會不同(在幾何習題中,參數的變化可能會改變圖形的形狀,結果自然也就隨之變化). 3)根據實際問題找出隱藏條件,然后進行分類討論,如分組問題、實際應用題等.討論是要有原因的,有些實際問題就是分段的,因此解決這類問題就要分類討論.分類是客觀存在的,但不是絕對的,分類的方法不是唯一的,只需要考慮所有的情況就可以. 1.2.2準確找分界點,“扁平化”處理[3] 有時討論的對象不是一個,而是多個,或者在分類討論時,分類的情況中還需要分類,這樣的解題過程就會極其繁瑣冗長.解決這樣的題目,就需要進行正確的分類討論,而如何讓分類討論的層次最少,是我們要努力去發掘的.第一步,就是確認一個正確恰當的分界點,把題目分為幾個部分,逐步進行解決;第二步就是在分類里再分類討論.我們要牢記:同級討論是平等的,沒有等級之分,不能遺漏,更不能重復,才是真正的恰當分類. 恰當分類討論,首先要搞清楚根據什么進行分類,只有明白了分類的原因,才能正確分類,再根據分類中的主要和次要方面進行討論. 1)略; 2)用min{m,n}表示m,n中的最小值,設函數h(x)=min{f(x),g(x)}(其中x>0),討論h(x)零點的個數. (2015年全國數學高考卷Ⅰ理科試題第21題) 分析該題第2)小題分類討論的第一層是主元素x,第二層是參數a. ①當x>1時,g(x)=-lnx<0,從而 h(x)=min{f(x),g(x)}≤g(x)<0, 此時h(x)無零點. ②當x=1時, h(x)=min{f(x),g(x)}=0, 則h(x)無零點. ③當0 f′(x)=3x2+a, 因為0 評注當分類比較明確時,第一步是把相同的地方先計算出來,否則分類討論后就會需要進行重復計算,分清分類討論的主次關系,分類分不好會大大加大計算量,使題目復雜化. 當題目較復雜時,應該進行多次多層分類討論,在進行并列多次多層討論時,首先應該找到分類的分界點,再采用合適的方法對各分界點進行分析討論,注意討論的范圍和條件,才能進行正確的分析和討論. 例2設f(x)=xlnx-ax2+(2a-1)x,其中a∈R. 1)令g(x)=f′(x),求g(x)的單調區間; 2)已知f(x)在x=1處取得極大值,求實數a的取值范圍. 1)分析求導得f′(x)=lnx-2ax+2a,從而 g(x)=lnx-2ax+2a,其中x∈(0,+∞), 于是 討論a≤0,a>0這兩種情況下導函數的正負號,確定函數的單調區間. 評注若一道題目較復雜,需要進行多層次多角度的分類討論時,則要根據題目涵蓋的條件找出分界點,從不同的層次、不同的角度進行分類討論,盡可能找到分類較少的層次,做到簡化討論,快速而準確地答題.若需要解決的是單個參數問題,則分界依據以選擇數軸為最佳;若需要解決的是含有兩個參數的問題,則以平面區域來分界為最佳. 著名數學家華羅庚說過:“數缺形時少直觀,形少數時難入微,數形結合百般好,隔離分家萬事休.”在解題過程中,要注意培養自己數形結合方法的使用和挖掘,把問題簡化. 2)分析因為f′(1)=0,所以f(x)=lnx+2a(1-x)>0在(0,1)上恒成立,g(x)=lnx+2a(1-x)<0在(1,+∞)上恒成立,即 圖1 評注當含有變量的問題很難直接進行分類討論時,可從參數角度考慮解決,運用參數分離思想常常可以減少甚至避免分類討論.對于單變量問題,常直接變量分離;對于多變量問題,常利用幾何特征進行“相對變量分離”,運用其幾何特征求解. 例3已知函數f(x)=a·9x-2a·3x+1-b(其中a>0)在區間[0,1]上有最大值5以及最小值1. 1)求a,b的值; 2)若不等式f(x)-k·9x≥0在x∈[-1,1]上有解,求實數k的取值范圍. 分析1)a=1,b=-2(過程略). (1-k)·t2≥2t-2, 亦即 h(m)=-m2+m, 則 從而 h(m)min=h(3)=-32+3=-6, 于是 1-k≥-12, 故 k≤13. 評注變量分離法應該避開分類討論的鋒芒,“相對變量分離法”要求靈活利用幾何模型,轉換成立體模型進行解答. 分類討論應盡可能地減少層次甚至一步到位,讓人對結果一目了然,結構分明,分類簡單清楚,邏輯性強.抓住題目中給出的條件進行分析,合理使用題目中隱含的限制條件,合理使用合理分類,最大程度地簡化分類范圍,簡化解題過程.這樣對于快速解題、提高正確率至關重要. 1.已知函數y=x2-4x+1的定義域為[1,t],在該定義域內函數的最大值與最小值之和為-5,則實數t的取值范圍為 () A.(1,3] B.[2,3] C.(1,2] D.(2,3) 2.一個工人照看3臺機床,在一小時內,甲、乙、丙這3臺機床需要照看的概率分別為0.9,0.8,0.85,在一小時內,至少有一臺機床不需要照看的概率為______. 4.設k為實數,求方程x4-2kx2+k2+2k-3=0的實數x的取值范圍. 5.解關于x的不等式:ax2-(a+1)x+1<0. 6.已知函數f(x)=-ln(x+b)+a(其中a,b∈R). 1)若y=f(x)的圖像在(2,f(2))的切線方程為y=-x+3,求a,b的值; 參考答案 4.分析將原方程整理為關于k的二次方程k2+2(1-x2)k+x4-3=0.因為k是實數,所以 Δ=4(1-x2)2-4(x4-3)≥0, 即 2-x2≥0, 解得 5.分析1)當a=0時,原不等式化為-x+1<0,故x>1. 2)當a≠0時,原不等式化為 ②若a>0,則原不等式化為 6.分析1)由f(x)=-ln(x+b)+a,得 從而 得 a=1,b=-1. 從而 即 故 [1]梁莎.湖南省高考數學(理科卷)試題研究[D].長沙:湖南師范大學,2014. [2]李裕青.高考數學分層復習的實踐研究[D].廣州:廣州大學,2013. [3]馮海容,江強.恰當分類與減少討論層次的策略[J].中學教研(數學),2017(5):32-37.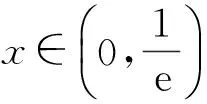
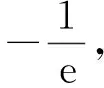
2 利用洛必達法則進行優化
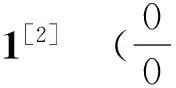
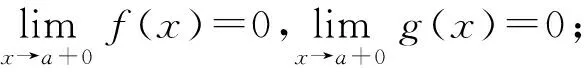
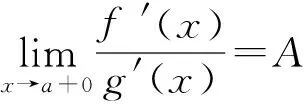

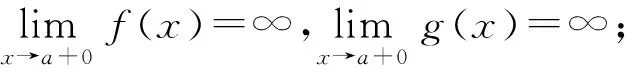
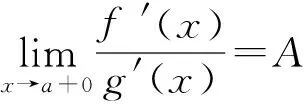
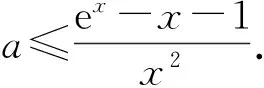
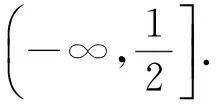
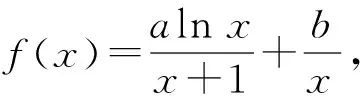
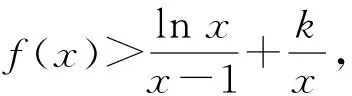
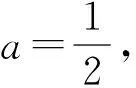
3 利用函數極限的局部保號性進行優化
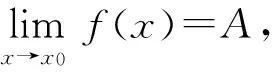
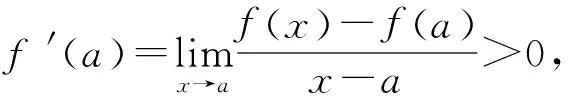

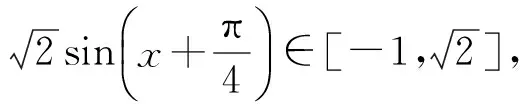
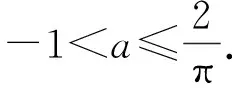
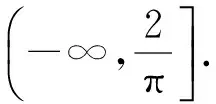
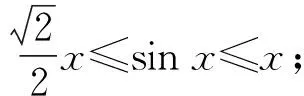
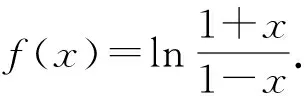
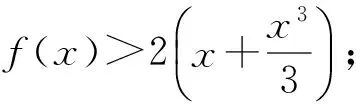
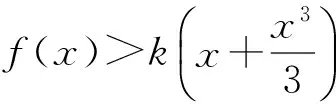
2 典題剖析
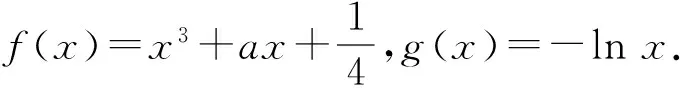
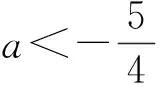
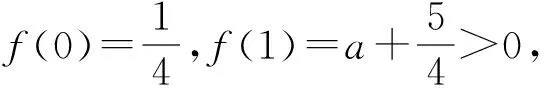
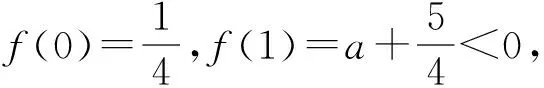
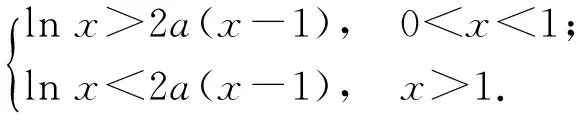
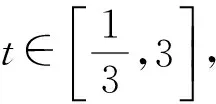
3 精題集萃