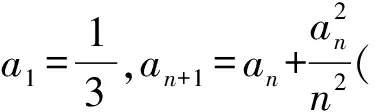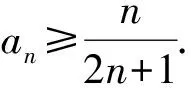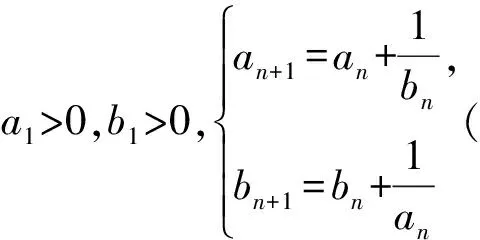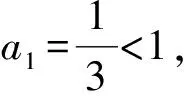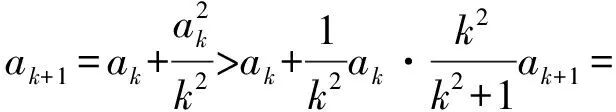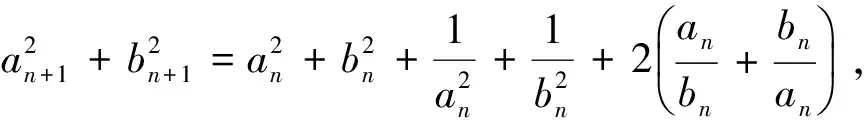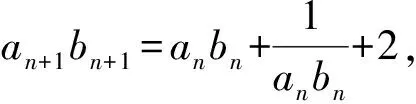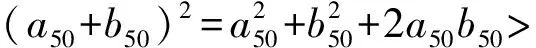數(shù)列與數(shù)學(xué)歸納法
●
(杭州市基礎(chǔ)教育研究室,浙江 杭州 310003)
數(shù)列與數(shù)學(xué)歸納法
●王紅權(quán)
(杭州市基礎(chǔ)教育研究室,浙江 杭州 310003)
數(shù)列是歷年數(shù)學(xué)高考重點(diǎn)考查的內(nèi)容之一,浙江省的數(shù)列試題既重視基礎(chǔ)又強(qiáng)調(diào)關(guān)聯(lián),客觀題立意概念的本質(zhì),綜合性試題對學(xué)生的素養(yǎng)要求很高,不僅要有較強(qiáng)的估算和運(yùn)算能力,還要求有敏銳的判斷力.文章舉例分析近幾年浙江省數(shù)學(xué)高考對數(shù)列的考查,列舉所考查的內(nèi)容、常用方法和命題方向等.
復(fù)習(xí)備考;數(shù)列;數(shù)學(xué)歸納法;不等式
1 知識內(nèi)容
數(shù)列和數(shù)學(xué)歸納法內(nèi)容涵蓋:數(shù)列的概念和表示法;等差和等比數(shù)列的概念、通項(xiàng)公式和求和公式、與一次函數(shù)和指數(shù)函數(shù)的關(guān)系、簡單應(yīng)用;可以利用錯位相減法求和的數(shù)列;數(shù)學(xué)歸納法等.
2 命題分析
2012—2017年數(shù)列試題題量、總分值和知識點(diǎn)的分布如表1所示.
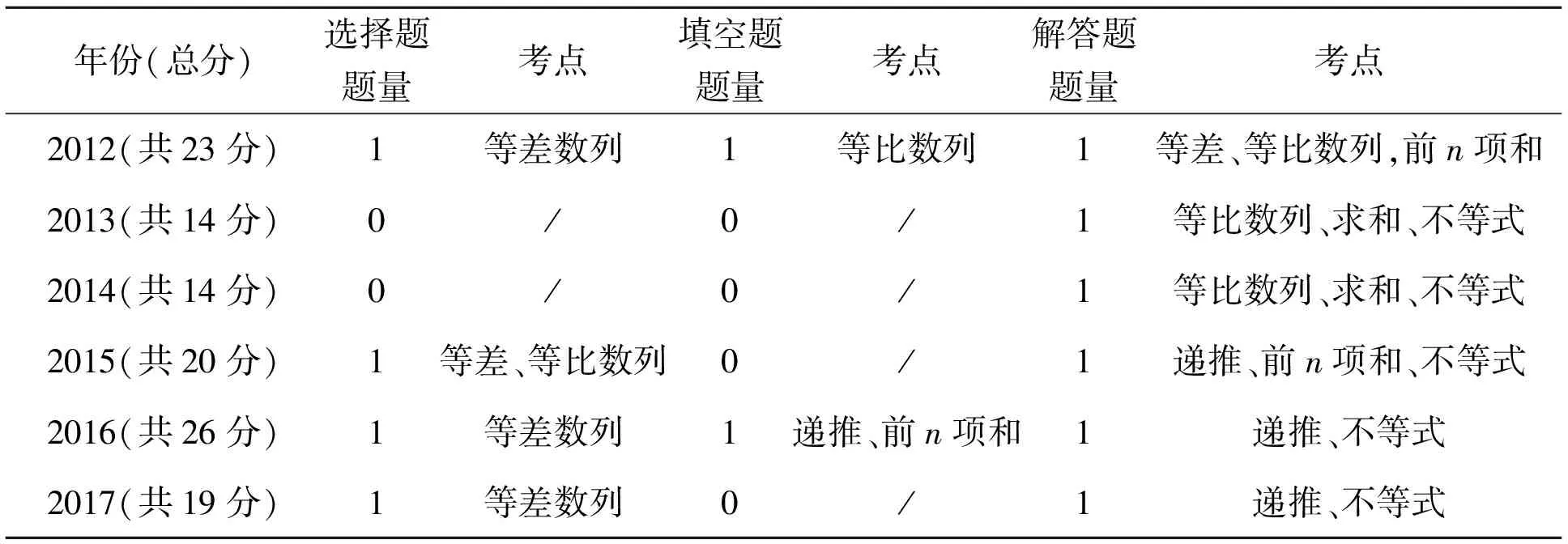
表1 2012—2017年數(shù)列試題題量、總分值和知識點(diǎn)的分布情況
從表1觀察,數(shù)列試題考查內(nèi)容較為穩(wěn)定,涉及等差和等比數(shù)列的定義、通項(xiàng)公式和求和公式,可化為等差或等比數(shù)列的數(shù)列求和、數(shù)列的遞推公式以及不等式相關(guān)的綜合性問題等.但從總分值分布的角度看,隨年份的波動較大;從題型分布看,也具有較大的不確定性.
從題目功能看,選擇題一般考查對概念的理解,要求考生判斷出正確的選項(xiàng),不需要做過多的運(yùn)算;填空題則要求在理解概念的基礎(chǔ)上,選擇適當(dāng)?shù)乃惴ú⒄_求解;解答題則強(qiáng)調(diào)綜合,但2012—2014年和2015—2017年的試題存在顯著的差異,前者命題的立意以數(shù)列基本性質(zhì)的綜合為主,后者則以遞推公式為基礎(chǔ),主要考查的是不等式的性質(zhì),綜合性和難度顯著提高.
3 典題剖析
考點(diǎn)1等差和等比數(shù)列的基本問題.
以等差和等比數(shù)列的概念、通項(xiàng)公式和求和公式為基礎(chǔ),利用基本量法求解,是高考考查數(shù)列內(nèi)容的方向之一.這類問題要求考生熟悉定義,合理選擇,計(jì)算準(zhǔn)確.
例如:復(fù)習(xí)等差數(shù)列的通項(xiàng)公式、求和公式,理解等差數(shù)列基本問題的求解策略:“知三求二”.例1以表格的形式給出問題,可以更直觀地感知基本量是求解等差數(shù)列問題的基本方法.等比數(shù)列類似.
例1[1]已知數(shù)列{an}是等差數(shù)列,根據(jù)表2中已有的信息完成其他信息.
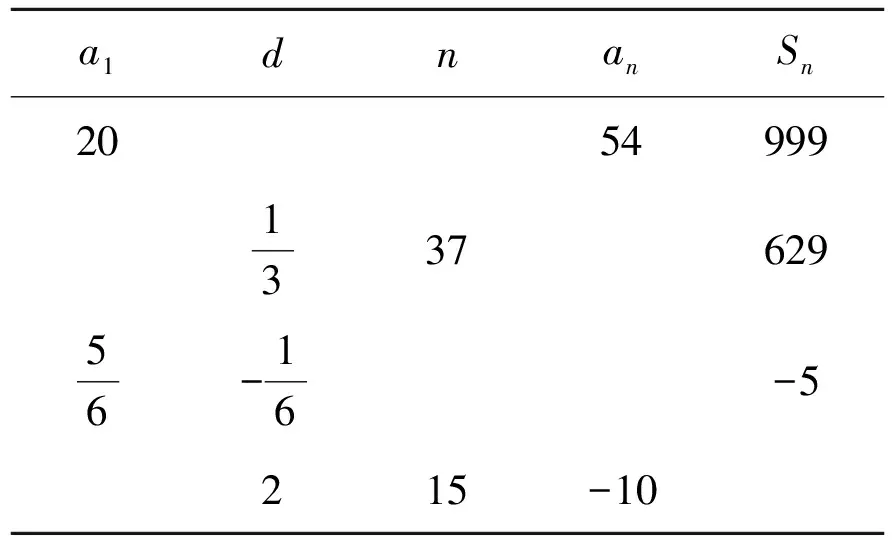
表2 等差數(shù)列{an}的相關(guān)信息
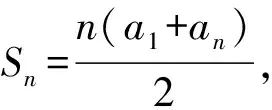
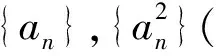
( )
A.60 B.62 C.63 D.66
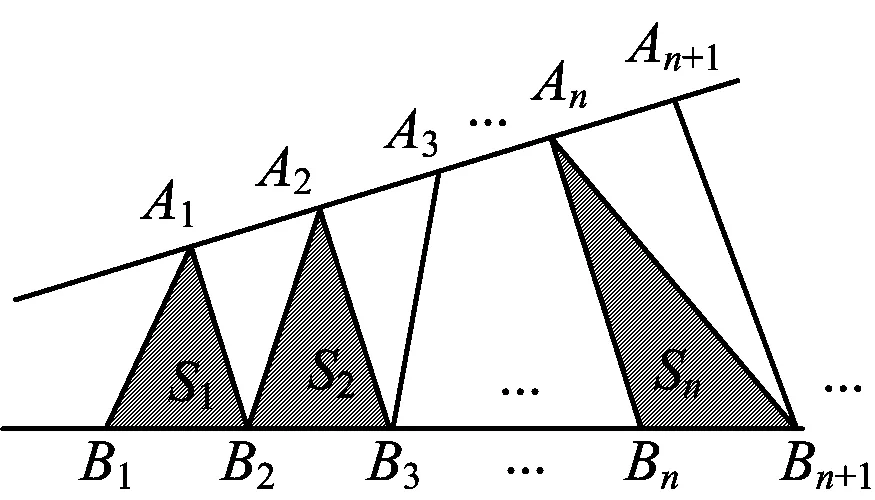
圖1
(2014年浙江省高中數(shù)學(xué)學(xué)考試題第22題)
2)如圖1,點(diǎn)列{An},{Bn}分別在某銳角的兩邊上,且|AnAn+1|=|An+1An+2|,An≠An+2,其中n∈N*;|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,其中n∈N*,P≠Q(mào)表示點(diǎn)P與點(diǎn)Q不重合.若dn=|AnBn|,Sn為△AnBnBn+1的面積,則
( )
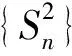
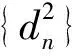
(2016年浙江省數(shù)學(xué)高考理科試題第8題)
3)已知等差數(shù)列{an}的公差為d,前n項(xiàng)和為Sn,則“d>0”是“S4+S6>2S5”的
( )
A.充分不必要條件 B.必要不充分條件
C.充分必要條件 D.既不充分也不必要條件
(2017年浙江省數(shù)學(xué)高考試題第6題)
分析這類問題可以選擇利用定義和基本量計(jì)算進(jìn)行解決,但性價比不高.
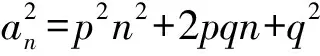
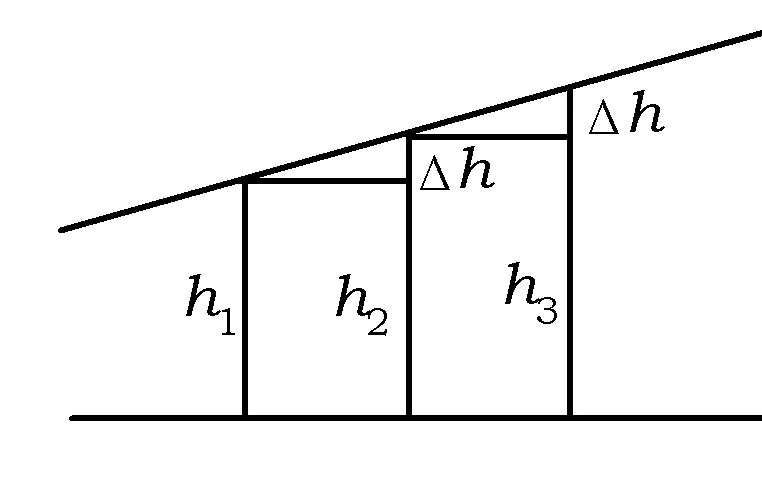
圖2
2)由三角形的面積想到高線,由于所有的三角形都等底,因此只需要考查圖2中的高線hn組成的數(shù)列{hn},根據(jù)圖2,顯然{hn}是等差數(shù)列,這便是等差數(shù)列的幾何模型,直觀而且本質(zhì).
3)思路1已知條件可變形為
S4-S5>S5-S6,
即
a5 從而d>0,反之亦然.故選C. 思路2已知條件可變形為 學(xué)習(xí)數(shù)列當(dāng)從數(shù)入手,利用代數(shù)手段精準(zhǔn)刻畫其變化規(guī)律,利用其函數(shù)背景揭示數(shù)列的本質(zhì),特別是等差數(shù)列還可以輔之以幾何直觀幫助理解,揭示知識間的內(nèi)在聯(lián)系[2].第1)小題和第2)小題較好地考查了等差數(shù)列通項(xiàng)公式的線性特征,其中第1)小題從函數(shù)的角度給出了刻畫,第2)小題用幾何直觀加以刻畫,深刻而本質(zhì);第3)小題用函數(shù)對等差數(shù)列的前n項(xiàng)和公式給出了函數(shù)刻畫,揭示其非線性特征.只要深刻理解其本質(zhì),并不依賴計(jì)算,這也是浙江卷選擇題的最大特點(diǎn). 考點(diǎn)2可化為等差和等比數(shù)列的問題. 由遞推公式得出數(shù)列變化規(guī)律是解決數(shù)列問題的常見方法之一,若題干中出現(xiàn)了一般數(shù)列的遞推公式,則可以考慮轉(zhuǎn)化為等差或等比數(shù)列的遞推公式.常見的有兩類:一類是低階線性遞推關(guān)系;另一類是以分式形式出現(xiàn)的遞推關(guān)系,通過適當(dāng)?shù)淖冃危苫癁榫€性遞推或直接轉(zhuǎn)化為等比數(shù)列. 例31)已知數(shù)列{an},{bn}滿足:a1=-1,b1=2,an+1=-bn,bn+1=2an-3bn(其中n∈N*),則b2 015+b2 016=______. bi+2+bi+1=-2(bi+1+bi), 從而數(shù)列{bi+1+bi}是以b1+b2=-6為首項(xiàng)、-2為公比的等比數(shù)列,于是 b2 015+b2 016=-6×(-2)2 015=3×22 016. 2)由已知得到 從而 即 類似地,有 即 兩邊取對數(shù),得 因此 即 故取jn=2n-1即可. 注適當(dāng)?shù)淖冃问墙鉀Q這類問題的關(guān)鍵,往什么方向變形,心中要有基本的模型,如線性遞推an+1=an+p可以構(gòu)造等比數(shù)列,分式形式兩邊取倒數(shù)可以構(gòu)造等差或等比數(shù)列,指數(shù)形式an+1=panq(其中p>0,an>0)兩邊取對數(shù)可以構(gòu)造等比數(shù)列. 考點(diǎn)3數(shù)列與不等式相關(guān)的問題. 數(shù)列是特殊的函數(shù),函數(shù)的很多性質(zhì)需要用不等式加以刻畫,數(shù)列和不等式結(jié)合的相關(guān)問題在近3年浙江省數(shù)學(xué)高考命題中均作為壓軸題出現(xiàn),考查的重心由數(shù)列常用性質(zhì)轉(zhuǎn)移到遞推公式的復(fù)雜變形和不等式的證明. (2016年浙江省杭州市第二次質(zhì)量檢測數(shù)學(xué)試題第18題) (2015年浙江省數(shù)學(xué)高考理科試題第20題) 所以數(shù)列{an}單調(diào)遞增,從而an≥a1=1,于是 即 事實(shí)上, (1) 即 (a1-a2)+…+(an-an+1)= 同第1)小題分析可知 所以 累加得 從而 an-an+1≥anan+1, 即 累加得 即 由第①小題得an≤2an+1, 從而 即 累加得 于是 即 注1第1)小題和第2)小題雖然都是構(gòu)建“差結(jié)構(gòu)”,但兩個問題之間還是有區(qū)別的:第1)小題是通過恒等變形建構(gòu)“差結(jié)構(gòu)”;第2)小題既可以通過恒等變形建構(gòu),也可以通過放縮獲得中間結(jié)構(gòu),然后化為“差結(jié)構(gòu)”,其實(shí)這樣的放縮更接近浙江省數(shù)學(xué)高考試卷中的數(shù)列不等式證明的本質(zhì),如2008年和2017年的浙江省數(shù)學(xué)高考壓軸題是完全一樣的思路.當(dāng)然第2)小題也可以用數(shù)學(xué)歸納法證明,請讀者自己完成. 注2沒有“差結(jié)構(gòu)”就沒有“前n項(xiàng)和”,換言之,在遞推公式立意的試題中,有“和”就需要關(guān)注“差結(jié)構(gòu)”. 1.若一個等差數(shù)列前3項(xiàng)的和為34,最后3項(xiàng)的和為146,且所有項(xiàng)的和為390,則這個數(shù)列有 ( ) A.13項(xiàng) B.12項(xiàng) C.11項(xiàng) D.10項(xiàng) 2.某種細(xì)菌在培養(yǎng)過程中,每20分鐘分裂一次(一次分裂為兩個),經(jīng)過3個小時,這種細(xì)菌由一個可以繁殖成 ( ) A.511個 B.512個 C.513個 D.1 024個 3.設(shè){an}是等差數(shù)列,Sn為其前n項(xiàng)的和.若正整數(shù)i,j,k,l滿足i+j=k+l(其中i≤k≤l≤j),則 ( ) A.a(chǎn)ial≤ajakB.a(chǎn)ial≥ajak C.SiSl≤SjSkD.SiSl≥SjSk 4.已知等差數(shù)列{an},等比數(shù)列{bn}的公比為q(其中n,q∈N*),設(shè){an},{bn}的前n項(xiàng)和分別為Sn,Tn.若T2n+1=Sqn,則an=______. 5.已知數(shù)列{xn},滿足(n+1)xn+1=xn+n,且x1=2,則x2 018=______. 1)證明:an 參考答案 1.A 2.D 3.A 6.證明1)易知an>0,從而 于是 進(jìn)而 因此,當(dāng)n≥2時, 故 an<1. an<1(其中n∈N*), 于是 an 2)當(dāng)n=1時,顯然成立.由an<1,知 從而 即 因此,當(dāng)n≥2時, 即 故 4+4×49=200. 200+200=400, 因此 a50+b50>20. [1] 鄔建云,王紅權(quán).“等差數(shù)列”習(xí)題課的教學(xué)實(shí)踐[J].中國數(shù)學(xué)教育,2015(12):25-30. [2] 王紅權(quán),王凱.聚焦新特點(diǎn) 研究新策略——2017年浙江省數(shù)學(xué)新高考復(fù)習(xí)備考研究[J].教學(xué)月刊,2017(5):47-52. 收文日期:2017-10-30; 2017-12-02 王紅權(quán)(1970-),男,浙江杭州人,中學(xué)高級教師.研究方向:數(shù)學(xué)教育. O122.4 A 1003-6407(2018)03-0037-05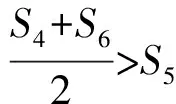
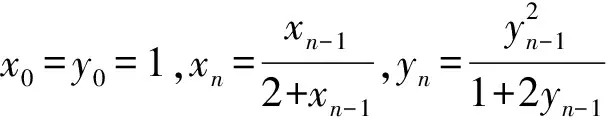
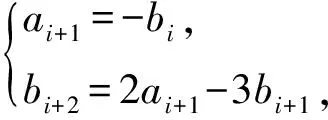
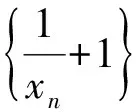
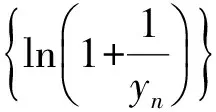
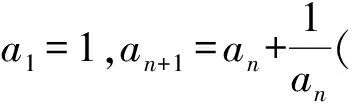
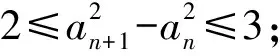
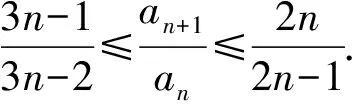
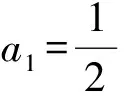
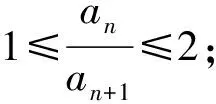
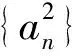
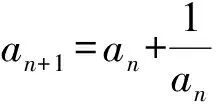
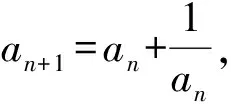
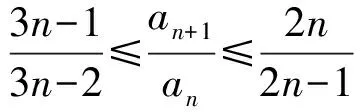
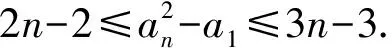
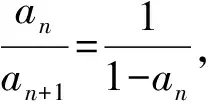
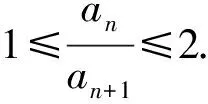
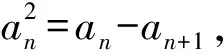
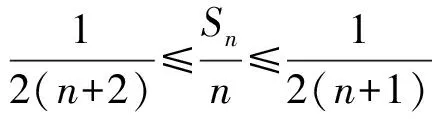
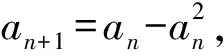

4 精題集萃