在說題中感悟 在說題中提升
——參加教師基本功大賽有感

●

(石門中學,廣東 佛山 528248)

在說題中感悟在說題中提升
——參加教師基本功大賽有感

●徐守軍

(石門中學,廣東 佛山 528248)

文章通過自身參加教師說題比賽的經歷，探討當下流行的教研方式，具體展現了“什么是說題，為什么說題，說題說什么”，以達到在說題中感悟和提升的目的.

說題;感悟;提升

教師說題是類似于說課的一種新的教研活動，是說課的延續和創新，是一種教育教研展示和討論活動.表面來看，說題是教師在“說”數學知識的前后聯系、求解題目的方法和策略，其實質展現的是教師自身數學教育的理論功底、數學知識的掌握程度、數學方法的理解能力及數學教學的理念[1].

1 說題是什么

解數學題的本質是要找到并且規范而簡明地表述出從題目的已知條件到要求目標的一系列命題轉化的一條通路.簡而言之，說題就是利用教學語言口述探尋解題通路的思維過程以及所采納的數學思想方法和解題策略[2].說題作為一種新的教研方式，正在被越來越多的教師接受.

2 為什么說題

說題可以將教研內容的范圍逐漸縮小，是一種深層次備課后的展示，提高了課堂教學的有效性，體現了以小見大、去虛務實的教研理念．說題，能促進教師對教材例習題和高考試題的研究，從而更好地把握教材和高考命題的方向，提高數學課堂教學的針對性和有效性，能更好地反映教師的基本功，啟發和引導教師深層次的備考，促進教師專業成長.

3 說題說什么

通常，說題包含以下6個方面：題目的考查目標、難度分析、題意理解和解題策略、教法和學法、題目的價值及推廣、教學反思.下面筆者結合自己參加廣東省佛山市首屆教師說題大賽的情況，談談如何說題.

3.1 說題目及考查目標

例1正項數列{an}的前n項和Sn滿足:

1)求數列{an}的通項公式；

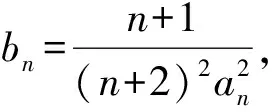
該題目源自2013年江西省數學高考理科試題第17題，考查數列通項公式與前n項和的關系、含有字母的一元二次方程解法以及特殊數列求和、證明不等式等知識.本題對學生的觀察能力、運算能力、理解能力、轉化能力和表達能力等有較高的要求，體現了猜想與論證的思想、方程思想、轉化與化歸思想等.

3.2 說重難點

本題以知識和方法立意，兼顧能力的考查，重點考查數列基礎和主干知識，屬于高考中的中高檔題.第1)小題考查了已知前n項和求通項，難點在于方程的處理；第2)小題考查特殊數列求和及不等式的證明，難點在于裂項求和的運用——如何構造裂項，如何處理復雜多項式及分式運算.

3.3 說題意理解和解題策略

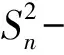
第1)小題的切入點是抓住已知式本質：關于Sn的一元二次方程，利用解方程的方法求出Sn，重點考查含字母的一元二次方程解法，考查由前n項和求通項的基本知識，關鍵點在于如何想到解方程的途徑.具體解答如下：

1)解法1(十字相乘法)已知式可化為

(Sn+1)[Sn-(n2+n)]=0.

因為Sn+1>0，所以

Sn=n2+n.

當n≥2時，

an=Sn-Sn-1=2n，

當n=1時，a1=S1=2滿足an=2n，因此

an=2n(其中n∈N*).

說明1)能否觀察到方程的特點，并用十字相乘法求解是關鍵；2)由Sn求an是對基礎知識的考查，可能會忽視當n=1時的情況.

解法2(求根公式法)由已知可得

化簡可得(略).

解法3(歸納猜想法)將n=1代入已知式,得

解得

S1=2，

從而

S2=6，S3=12,

于是

a1=2,a2=4,a3=6，…

猜想：an=2n(其中n∈N*)，并證明(略).

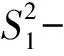
第2)小題的切入點是對bn進行變形，利用bn求出Tn，重點考查特殊數列求和方法——裂項相消法，關鍵點在于如何想到裂項、怎樣裂項，這也是大多數學生無法完成此題的最主要原因.

2)證明(裂項求和)因為an=2n,所以

說明1)想到裂項的方法是關鍵，如何裂項是難點；2)在消去相同的部分運算時極易出現多項或少項的情況，建議采取分組的方法，如

4 說教法與學法分析

美國當代數學家哈爾斯說過：“問題是數學的心臟.”沒有好的問題就沒有異彩紛呈的數學，沒有好老師用好的問題引領學生去學，就沒有精彩的數學課堂.

4.1 立足于學生答題的情況，分析學生存在的問題

從學生作答的情況來看，本題的得分并不高，值得注意的有以下問題：1)第1)小題中不懂巧妙利用十字相乘法求解；2)第2)小題中求和時不知采用哪種方法；3)運算速度和準確度普遍有待提高；4)注意解答規范和細節，如當n=1時的情況不要忘記.

4.2 教會學生如何分析題目的定位和目標

從題目的位置來看，本題處于第17題的位置，應屬于中等難度的考題；從題目的已知條件和結論來看，本題的本質是回歸課本所學核心和主干知識.因此在平時的學習過程中應立足基礎知識和基本關聯，搞清概念本質和必然聯系.如

的裂項看似巧合，實則必然.

4.3 搞清楚問題的本質和所學知識的關聯

對于數列不等式的證明問題通常分為可求和與不可求和兩大類，可求和的直接求和再比較大小，不可求和的常用放縮法(也有其他比如數學歸納法、構造控制數列法、利用加強不等式、積分法等).求和常見的方法有公式法、拆項分組法、裂項相消法、錯位相減法和倒序相加法，本題只有裂項相消法適用.

4.4 解法溯源，分析思路

這么復雜的式子如何裂項呢？1)由于分母已因式分解，實際作通分的逆運算即可，不用去擔心分子n+1如何處理，它一定有它存在的理由.如果掌握好這些知識和聯系，解好這道題就是水到渠成的事情了.2)對于分母已分解因式，除了可用通分逆運算，還可采用待定系數(配湊)，即將分子n+1，配成分母n2，(n+2)2的關系，若無法配湊，則要放縮，如

3)若分母無法分解因式，則可采用添補技巧或放縮,從而達到裂項的目的.4)根據微分中值定理實現裂項過程，如

雖然本題無需放縮，可直接裂項，但有一點我們可以確定的是裂項后是-2次式，原式是-3次的，且裂項后的式子是原式的原函數，這點也為我們以后解決裂項問題明確了方向.

4.5 問題驅動，詳細剖析解題策略

對第1)小題可設計如下問題，引導學生思考：①已知Sn求an，通常如何求解？②已知的是Sn的關系式，即Sn不直接已知，如何求解？

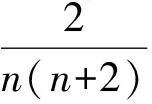
在解題的過程中要避免“會而不對，對而不全”的情況.因此，平時教學中要重點關注以下幾個方面：1)注意書寫表達規范；2)注意運算結果準確；3)注意條件與結論的等價轉換；4)注意分類討論要全面，不能想當然.

4.6 及時捕捉學生的閃光點

教學中需及時關注學生的反應，以及學生對題目的理解、解法等.比如：學生的巧妙解法，或者出發點是好的，即使沒做出來，也要借機肯定學生的想法，這對學生無疑是莫大的鼓勵，再解到此類問題時便能有信心、有毅力求出答案.

5 說題目的價值與推廣

從題目考查的深度與思維量來看，該題作為高考的中高檔題，注重考查基礎知識和基本技能，并在此基礎上有所提高，是一道好題.而作為平時教學，該題更是對教學有很好的導向作用，因此課堂教學要立足基礎，高于基礎，挖掘本質，探尋聯系，這也是素質教育的一種體現.在該題的教學中，教師可做以下幾個方面的推廣：

第1)小題中，求an的表達式，實質是考查對Sn的關系式的處理，需弄清問題的本質，關系式是方程還是遞推關系.此類題還有以下情形：

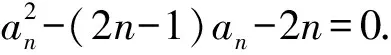
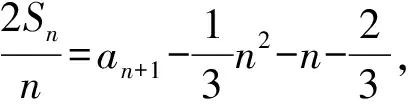
情形3已知Sn的遞推關系，如Sn+1=a2Sn+a1,其中n∈N*.

情形4已知an的遞推關系，如an+1=pan+q,其中n∈N*(這里q可改成關于n的式子).

第2)小題是裂項求和的問題，以原題為基礎可設計以下變式：

變式1(橫向變式)指數型

對數型

變式2(縱向變式)放縮型

變式3(能力提升)

充分發揮說題的功能，深入地挖掘題目、發展題目，就能更好地備考.

源于原題、高于原題，這是變式教學的重要指導思想.問題須在學生的“最近發展區”內進行拓展，以原題為源，緊扣教材，突出定義、定理、公式的重要價值，突出數學思想在分析解決問題中的重要作用，體現教材在高考中的導向性，體現對學生能力培養的重要作用.

6 說教學反思

在平時的教學中,教師要引導學生對題目進行拆解，對復雜結構進行變形，從而化繁為簡.要學會抓概念、抓本質、抓基本方法，以不變應萬變.更重要的是，應意識到教學生解題是毅力的培養，當學生求解難題時，應讓他學會敗而不餒，學會欣賞微小的進展，學會期待靈感的迸發，學會當靈感來臨后全力以赴.讓學生養成良好的思維習慣，樹立良好的思維品質，這才是真正的授人以漁.

[1] 傅瑞琦.說題，讓主題教研更精彩[J].中國數學教育，2012(3)：45-48.

[2] 成克利.中學數學教學中開展說題活動的實踐與認識[J].數學教育學報，2001，10(5)：32-34.

收文日期：2017-10-19；

2017-11-21

徐守軍(1982-)，男，江蘇南通人，中學一級教師.研究方向：數學教育.

O122.1

A

1003-6407(2018)03-0027-03