一道不等式題目的再探究

●

(洪家中學,浙江 臺州 318015)

一道不等式題目的再探究

●何再君

(洪家中學,浙江 臺州 318015)

文章以一道期末試題為例，剖析題目難點，從代數式外在的結構特征出發，聯系不等式的一些基本結構，挖掘出問題的內在聯系和解題規律,并通過類似題目和相關變式來研究此類問題中一些常見的解決方法，破解其思維過程，揭開其神秘面紗.

基本不等式;解題;結構特征;“1”的代換特征

1 問題的提出

( )

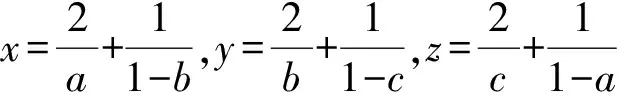
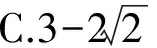
(2016年浙江省臺州市高二數學期末試題第14題)

2 解法探究

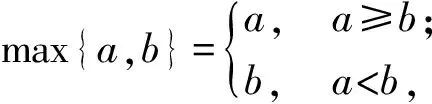
即例1實質上是求max{x,y,z}的最小值.

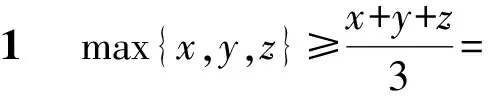
易看出分子的3個代數式結構一樣，字母的范圍一樣，因此只要分析清楚一個代數式即可.

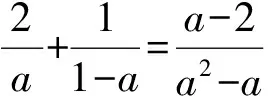
因為t∈(-2,-1)，由對勾函數的圖像得

所以

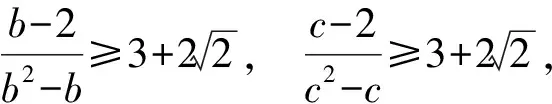
于是

故選B.

點評解法1的本質是通過換元轉化為熟悉的對勾函數，利用其函數圖像求最值.若涉及的函數比較復雜，且計算量大，則注意結合以往解題經驗，在轉化變形中識別結構模式，化繁為簡，去偽存真.

解法2max{x,y,z}≥

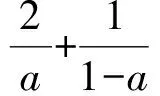
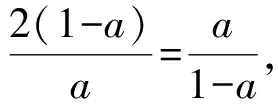
點評解法2的難點是不容易發現兩個分式的分母之和是常數1，還需聯想到“1”的代換,再利用基本不等式.

解法3可運用柯西不等式一步到位：

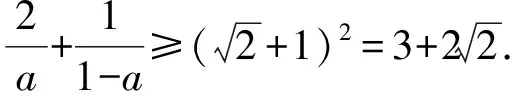
點評柯西不等式在高中選修教材中(不做要求)出現，若能適當應用，則將大大縮減解題時間.

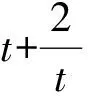
3 追根溯源，變式提升

仔細觀察代數式的形式，聯想曾經學過的知識中隱含的一些特殊結構與邏輯結構，將不熟悉的問題重組或分解成幾個小問題，然后各個擊破，找到聯系的橋梁，從而真正理解數學的內在本質.

3.1 “1”的代換特征再回首

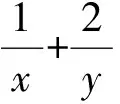
解因為

思考若把x+y=1改為2x+3y=2呢？原式可變為

后面的解法與例2相同.

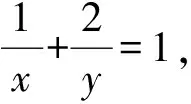
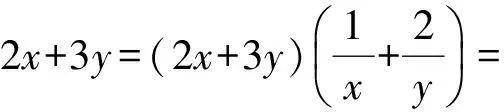
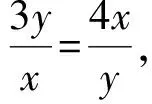
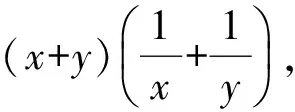
3.2 變式探究,提升思維

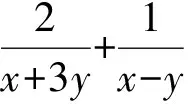
方法1觀察整式的結構特征以及分式結構的兩個分母，因為

(x+3y)+(x-y)=2(x+y)=2，

所以待求式可化為

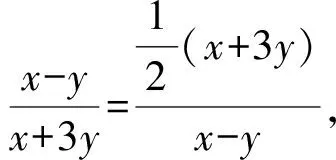
方法2受方法1啟發，可設x+y=λ(x+3y)+μ(x-y),則

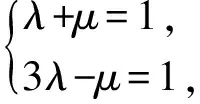
從而

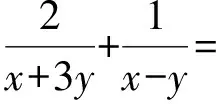
下面同方法1.

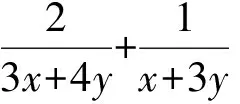
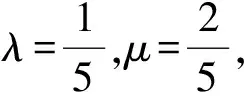
結論1當分式求和結構中分母的線性代數值和為定值,可利用基本不等式求分式和的最值.

4 識別特征，提高能力

例4已知a>0,b>0且滿足a+2b=2,若不等式abt+(t-2)a-b≤1恒成立，則實數t的取值范圍為______.

解對不等式abt+(t-2)a-b≤1進行參數分離得

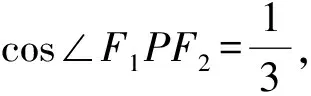
點評例4和例5的背景分別是不等式恒成立問題和圓錐曲線的離心率問題.去掉背景，可轉化為條件不等式求最值，看似復雜，實則利用常數“1”的變形與代數式結構重組，可快速解答.

總而言之，一個復雜的數學問題，當我們無從下手時，可想法設法把問題分解為幾個相關聯的小問題，各個擊破[3].在運算中善于挖掘代數式的結構特征，追本溯源，從而找到數學問題內在的邏輯鏈.

[1] 陳兒,楊亢爾.對一道統測試題的探源及拓展[J].中學教研(數學)，2017(4)：17-20.

[2] 李旺強.一道課本例題的解析、改編與變式[J].中學教研(數學)，2017(8)：27-29.

[3] 鄭良.析困難所在 覓破解良方[J].中學教研(數學)，2017(1)：26-30.

收文日期：2017-11-13；

2017-12-21

何再君(1982-)，女，浙江臺州人，中學二級教師.研究方向：數學教育.

O122.3

A

1003-6407(2018)03-0013-03