積累基本活動經(jīng)驗 提升數(shù)學(xué)核心素養(yǎng)
——由“三角函數(shù)與平面向量”測試結(jié)果引發(fā)的思考
●
(靈璧第一中學(xué),安徽 靈璧 234200)
●張 敏
(太倉高級中學(xué),江蘇 太倉 215400)
積累基本活動經(jīng)驗提升數(shù)學(xué)核心素養(yǎng)
——由“三角函數(shù)與平面向量”測試結(jié)果引發(fā)的思考
●鄭良
(靈璧第一中學(xué),安徽 靈璧 234200)
●張敏
(太倉高級中學(xué),江蘇 太倉 215400)
積累數(shù)學(xué)基本活動經(jīng)驗是培養(yǎng)學(xué)生數(shù)學(xué)核心素養(yǎng)的必由之路.文章以“三角函數(shù)與平面向量”周測題為載體,揭示學(xué)生共性現(xiàn)象的成因,同時針對教與學(xué)的現(xiàn)狀,結(jié)合教學(xué)實踐給出教學(xué)思考.
數(shù)學(xué)基本活動經(jīng)驗;數(shù)學(xué)核心素養(yǎng);比較;探究;整體
1 問題提出
近日,筆者所在學(xué)校年級組組織了“三角函數(shù)與平面向量”的周測.在隨后的學(xué)科組教研活動中,幾位年輕教師反映很多測試題(原題或變式)都在課堂上講過,但學(xué)生在測試中卻“答非所問”,并對后續(xù)的教學(xué)充滿困惑與迷茫.數(shù)學(xué)是常識的精微化,學(xué)生的共性學(xué)習(xí)行為往往是教師教學(xué)效果的外在表現(xiàn).如何讓學(xué)生理解并能靈活地運用這些常識(數(shù)學(xué)知識、思想方法等)是數(shù)學(xué)教師面臨的難題:課堂上學(xué)生參與了什么樣的活動,在活動中做了哪些觀察、操作、思考、認(rèn)識與理解;學(xué)生在體驗數(shù)學(xué)活動中產(chǎn)生的知識、技能和思想方法等是否升華為今后數(shù)學(xué)學(xué)習(xí)與問題解決的經(jīng)驗.下面僅以這次周測中部分試題為例,談?wù)劰P者對相關(guān)問題的理解,不足之處,敬請批評指正.
2 案例剖析
例11)在△ABC中,角A,B,C所對的邊分別為a,b,c,若B=60°,a=1,b=2,則sinA=
( )
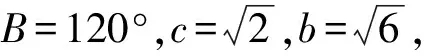
( )
分析(均為學(xué)生的想法,下同)兩個小題均為“已知三角形的兩邊和其中一邊的對角”解三角形,故可用正弦定理或余弦定理解答.
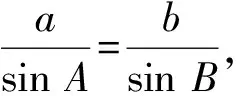
解法2由余弦定理得
c2-c-3=0,
從而
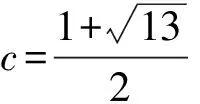
于是
得
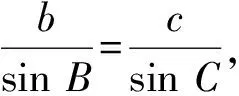
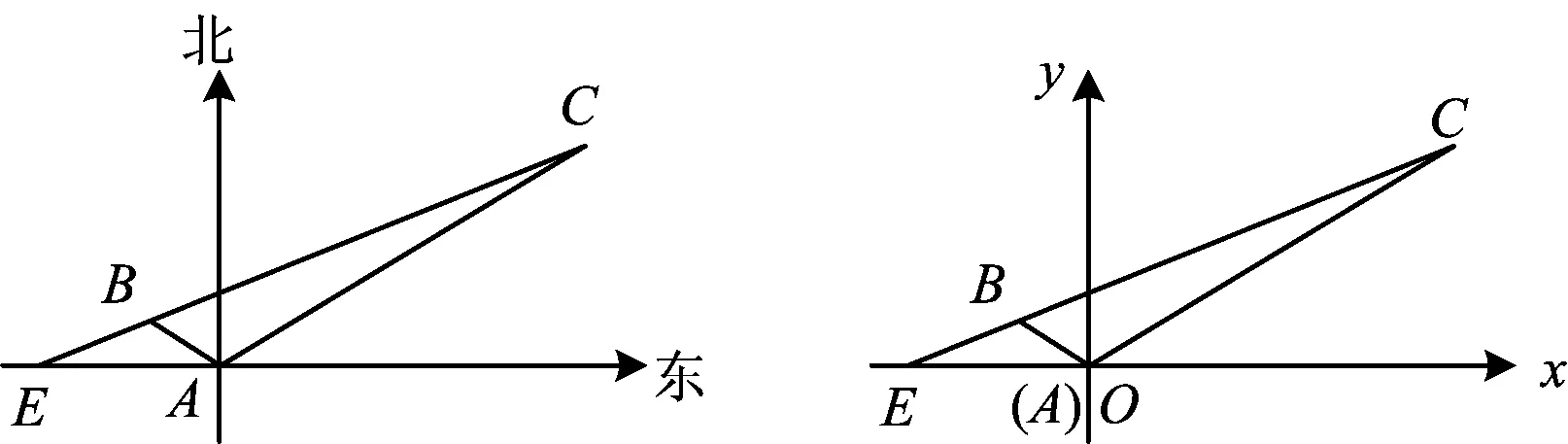
又c A=C=30°, 解法2由余弦定理得 評注雖然例1的兩個小題條件相同,但所求結(jié)論不同(分別為“另一邊的對角的正弦值”與“第三邊”).眾所周知,解決“已知三角形的兩邊和其中一邊的對角,求三角形的其他邊與角”常有兩種途徑:1)先由正弦定理求出另一邊對角的正弦,其次結(jié)合三角形中“大邊對大角”(或內(nèi)角和定理)確定該角,再確定第三個角,最后用正弦定理求出第三邊;2)根據(jù)方程思想用余弦定理求出第三邊,然后分別用余弦(或正弦)定理確定另外兩個角.教師在教授“解三角形”時常告訴學(xué)生:解三角形時,正弦定理適用于“已知兩角與任意一邊”和“已知兩邊和其中一邊的對角”,余弦定理適用于“已知三邊”“已知3個角”和“已知兩邊和其中一邊的對角”,很少引導(dǎo)學(xué)生去思考三角形的確定條件(至少3個獨立的要素)、解三角形為什么只學(xué)習(xí)正弦定理和余弦定理(兩個定理適用范圍囊括了確定三角形的各種情形)、“已知兩邊和其中一邊的對角”解三角形由哪個定理切入等問題,更沒有組織學(xué)生在數(shù)學(xué)活動中操作、體驗、思辨與提升,取而代之的是讓學(xué)生記住題型與解法,通過大量習(xí)題進(jìn)行“刺激反應(yīng)”(而非理性的模式識別),試圖在機(jī)械操練中提高運算速度. 與學(xué)生交流發(fā)現(xiàn),不少學(xué)生能夠辨識“題型”,在兩個小題中使用同樣的解題程序.對于第1)小題,運用正弦定理直達(dá)目標(biāo);對于第2)小題,運用余弦定理簡單快捷.教師要引導(dǎo)學(xué)生思考:為什么會出現(xiàn)負(fù)值;其意義是什么;還要讓學(xué)生認(rèn)識到本題的特性“A=C”,否則運用正弦定理事倍功半.學(xué)生對同一張試卷中重復(fù)(相鄰)出現(xiàn)相同問題置若罔聞,反映了學(xué)生的觀察能力、抽象概括能力、探究意識不強(qiáng),表明了學(xué)生的思維感性有余、理性不足.學(xué)生解題盲目性的根源就在于教師教學(xué)的淺表化、碎片化. 例2在△ABC中,AB=1,BC=2,則角C的取值范圍是______. 分析已知三角形的兩邊長,要構(gòu)成三角形,則第三邊必在某一范圍內(nèi),通過三邊又可表示三角形的任意一個內(nèi)角,由第三邊的取值范圍可以求出角的取值范圍. 解法1設(shè)AC=x,由構(gòu)成三角形的條件得1 x2-4xcosC+3=0. 令f(x)=x2-4xcosC+3,則f(x)=0在(1,3)之間有解,從而 f(1)·f(3)<0,(1) 由式(1),得 48(1-cosC)2<0, 無解;由式(2)得 又0 解法2設(shè)AC=x,由構(gòu)成三角形的條件得1 又0 評注“皮之不存,毛將焉附”,研究函數(shù)的性質(zhì)必先確定其定義域,解法1與解法2如是操作.解法1以x為主元研究函數(shù)f(x)的零點分布,求解過程中不少學(xué)生遺漏了f(x)的一個零點x1=1(或x1=3),另一個零點x2在(1,3)內(nèi)的情況,也有少數(shù)學(xué)生注意到x1x2=3這個特性.對于含參數(shù)的方程在某區(qū)間有解問題往往可以分離參數(shù)轉(zhuǎn)化為新函數(shù)的值域問題,解法2如是操作.由于y=cosx在(0,π)上單調(diào)遞減,從而可建立函數(shù)值與自變量之間的一一對應(yīng)關(guān)系,這也是解法1與解法2備受學(xué)生青睞的原因,正弦定理因為要驗證解的個數(shù)而無人問津,果真如此嗎?形式促使本質(zhì)外顯,本質(zhì)推動形式內(nèi)蘊;直覺誘發(fā)邏輯,邏輯反哺直覺.兩者結(jié)合,相得益彰.教學(xué)時,不應(yīng)當(dāng)犧牲一個而把另一個捧到天上去,應(yīng)當(dāng)把每一個都用到該用的地方.而要做到這一點,就只有注意它們的相互關(guān)系、它們的相互補充[1]. 事實上,正弦定理、余弦定理、射影定理是等價的,我們解題時只需“就近上車”.如在△ABC中,A>B,從正弦定理角度有 A>B?sinA>sinB?a>b; 從余弦定理角度有 A>B?cosB>cosA ?(a-b)(a+b+c)(a+b-c)>0 ?a>b. 本題中,若將A(其中A>C)視為已知,則問題可轉(zhuǎn)化為“已知三角形的兩邊和其中一邊的對角,求另一邊的對角”,由例1的分析可知用正弦定理簡單快捷.相比例2,例1的第1)小題只是三角形其中一邊對角的一種特殊情況(固定狀態(tài)),形式不同,本質(zhì)相同,相互聯(lián)系便可構(gòu)建整體,深化認(rèn)知. 解法1由正弦定理得 (3) (4) 式(3)×sinC-式(4)×cosC,得 即 于是 圖1 解法2如圖1,在邊AB上取一點D,使AD=CD=x,則 ∠DCB=∠BCA-∠A. 在△BCD中,由余弦定理得 解得x=5,從而 例4如圖2,某海島上一觀察哨A上午11時測得一輪船在海島北偏東60°的C處,12時20分時測得該輪船在海島北偏西60°的B處,12時40分該輪船到達(dá)位于海島正西方且距海島5千米的E港口,如果輪船始終勻速直線航行,則船速是多少(結(jié)果保留根號)? 圖2 圖3 分析由勻速直線運動的時間比可得其路程之比.利用解析法鎖定點B,C的位置. 則 解法2由題意得BC=4BE.設(shè)BE=x,則BC=4x,由已知得∠BAE=30°.在△AEC中,由正弦定理得 即 在△ABC中,由正弦定理得 即 在△ABE中,由余弦定理得 評注多數(shù)學(xué)生無法通過審題建立條件與結(jié)論的(三角)聯(lián)系導(dǎo)致無的放矢,只能借助解析法,將數(shù)學(xué)推理演變?yōu)閿?shù)學(xué)運算.在解法1中,不少學(xué)生沒有直接運用點B,C各自橫坐標(biāo)與縱坐標(biāo)的關(guān)聯(lián),而是先設(shè)元后再消元,使得過程冗余.少數(shù)學(xué)生結(jié)合平面幾何知識直接運用點B,C的縱坐標(biāo)之間的關(guān)系,優(yōu)化了解題過程.解法2以∠C為△AEC與△ABC的公共角建構(gòu)相互關(guān)聯(lián)的方程. 數(shù)學(xué)教學(xué)不只是教給學(xué)生數(shù)學(xué)知識、思想方法,還要教會學(xué)生如何思考,即探尋從無到有或從有到優(yōu)的思路,并能幫助學(xué)生理解數(shù)學(xué)本質(zhì).史寧中教授認(rèn)為:“通過基礎(chǔ)教育階段的數(shù)學(xué)教育,不管接受教育的人將來從事的工作是否與數(shù)學(xué)有關(guān),終極培養(yǎng)目標(biāo)都可以描述為:會用數(shù)學(xué)的眼光觀察現(xiàn)實世界;會用數(shù)學(xué)的思維思考現(xiàn)實世界;會用數(shù)學(xué)的語言表達(dá)現(xiàn)實世界.這‘三會’就是數(shù)學(xué)核心素養(yǎng).”[2]他還將“三會”具體化:數(shù)學(xué)的眼光就是數(shù)學(xué)抽象;數(shù)學(xué)的思維就是邏輯推理;數(shù)學(xué)的語言就是數(shù)學(xué)模型[2].“三會”是(信息攝入、信息加工、信息輸出)數(shù)學(xué)學(xué)習(xí)過程凝練的總結(jié).因此,積累數(shù)學(xué)基本活動經(jīng)驗是培養(yǎng)學(xué)生數(shù)學(xué)核心素養(yǎng)的必由之路. 數(shù)學(xué)活動經(jīng)驗是什么?數(shù)學(xué)教育專家及一線數(shù)學(xué)教師均提出不同的看法.如仲秀英老師認(rèn)為:學(xué)生數(shù)學(xué)活動經(jīng)驗可以理解為學(xué)生從經(jīng)歷的數(shù)學(xué)活動中獲得的感受、體驗、領(lǐng)悟以及由此獲得的數(shù)學(xué)知識、技能、情感與觀念等內(nèi)容組成的有機(jī)組合性經(jīng)驗[3].而張奠宙先生等認(rèn)為:數(shù)學(xué)活動經(jīng)驗是在數(shù)學(xué)目標(biāo)指引下,通過對具體事物進(jìn)行實際操作、考察和思考,從感性向理性飛躍時所形成的認(rèn)識[4]. 數(shù)學(xué)基本活動經(jīng)驗有助于學(xué)生數(shù)學(xué)活動的探究、數(shù)學(xué)思想方法的領(lǐng)悟、數(shù)學(xué)素養(yǎng)的提升.積累充足的數(shù)學(xué)活動經(jīng)驗是學(xué)好數(shù)學(xué)的重要基礎(chǔ).課堂是教學(xué)的主陣地,教師是學(xué)生的引領(lǐng)人.在數(shù)學(xué)教學(xué)中促進(jìn)并落實學(xué)生基本活動經(jīng)驗的積累,教師應(yīng)著眼以下方面. 教書育人,其核心是育人.體現(xiàn)在數(shù)學(xué)教學(xué)中,就是教師將數(shù)學(xué)的精髓(數(shù)學(xué)本質(zhì)、數(shù)學(xué)精神等)以易于學(xué)生理解與接受的方式傳遞給學(xué)生.章建躍博士提出“三個理解”,即理解數(shù)學(xué)、理解學(xué)生和理解教學(xué),它是數(shù)學(xué)教師專業(yè)發(fā)展的三大基石,也是教師進(jìn)行教學(xué)設(shè)計的基礎(chǔ). 如例1與例2中涉及正弦定理與余弦定理(及射影定理)的等價性,若教師沒有理解、掌握豐富的數(shù)學(xué)學(xué)科知識,則教學(xué)時只能照本宣科、淺嘗輒止;高中學(xué)生相對于教師來說,其知識匱乏、經(jīng)驗不足、精力分散(還要學(xué)其他科目)、認(rèn)知不完善,教師要在學(xué)生的最近發(fā)展區(qū)設(shè)置問題,促進(jìn)學(xué)生的理解.不少學(xué)生沒有認(rèn)識到例1與例2為同類問題,主要是因為其不能從運動變化的角度看問題,抽象思維能力有待提升;為了讓學(xué)生充分認(rèn)識到用正弦定理與余弦定理解決例1與例2的過程繁簡,教師可用思維導(dǎo)圖讓學(xué)生進(jìn)行感受、感知、感悟. 蒙臺梭利說過:“我聽過了,我就忘了;我看見了,我就記得了;我做過了,我就理解了.”著名教育家布魯納指出探究是教學(xué)的生命線.平鋪直敘的填鴨式教學(xué)只會使課堂成為一潭死水,教學(xué)效果可想而知,反之,教師設(shè)計合理的活動,讓學(xué)生在操作中思考、在合作中交流、在探究中思辨,學(xué)生的思維與認(rèn)知力必定在火熱的思考中得到完善與提升.教師可根據(jù)需要組織活動讓學(xué)生探究問題的一題多解、一題多變、多題一解,探究數(shù)學(xué)知識之間的內(nèi)在聯(lián)系,促進(jìn)構(gòu)建系統(tǒng)化的知識體系等. 探究過程需要良好的環(huán)境,“紀(jì)律和自由是一件事物不可分的兩部分——猶如一枚銅幣的兩面”[5].教師要控制良好的自由;探究目標(biāo)要適切,要根據(jù)具體情況及時把控探究的廣度、深度與高度,以免把探究變成了低效(甚至無效)活動或極個別人的表演. 《普通高中課程標(biāo)準(zhǔn)(實驗)》指出:“形式化是數(shù)學(xué)的本質(zhì)特征之一,在數(shù)學(xué)教學(xué)中,學(xué)習(xí)形式化的表達(dá)是一項基本要求,但不能只限于形式化的表達(dá),要強(qiáng)調(diào)對數(shù)學(xué)本質(zhì)的認(rèn)識,否則會將生動活潑的數(shù)學(xué)本質(zhì)淹沒在形式化的海洋里.”因此,數(shù)學(xué)教學(xué)要整合內(nèi)容,凸顯數(shù)學(xué)本質(zhì),滲透數(shù)學(xué)文化,弘揚理性精神,讓學(xué)生有充足的時間去思考、探究、感悟、評價、創(chuàng)造;數(shù)學(xué)教學(xué)要切實做到數(shù)學(xué)的形式化和數(shù)學(xué)本質(zhì)并重,形式化的表達(dá)要為揭示數(shù)學(xué)的本質(zhì)服務(wù);數(shù)學(xué)教育要充滿數(shù)學(xué)的“味道”. 例3以向量為表象,解三角形為本真,少數(shù)學(xué)生感性有余,理性不足,無法從表象中揭示本真,多數(shù)學(xué)生很難通過消元化歸得到解法1,更沒有想到構(gòu)造性解法2;例4涉及3個三角形,元素眾多,雜而不亂,更需要我們冷靜地思考、理性地謀劃;又如等差數(shù)列的通項公式an=a1+(n-1)d揭示了an的生成過程,凸顯了問題本質(zhì),而an=pn+q(其中p,q為常數(shù))是問題的形式化、一般化、抽象化.北京師范大學(xué)劉紹學(xué)教授反復(fù)強(qiáng)調(diào):“數(shù)學(xué)是自然的、數(shù)學(xué)是清楚的.數(shù)學(xué)教與學(xué)要通過追問促使理解自然、清楚、優(yōu)美.” [1] 鄭良.直覺和邏輯同行 形式和本質(zhì)并重——由一節(jié)公開課引發(fā)的思考[J].中國數(shù)學(xué)教育:高中版,2015(1/2):26-30. [2] 史寧中.高中數(shù)學(xué)核心素養(yǎng)的培養(yǎng)、評價與教學(xué)實施[J].中小學(xué)教材教學(xué),2017(5):4-9. [3] 仲秀英.促進(jìn)學(xué)生積累數(shù)學(xué)活動經(jīng)驗的教學(xué)策略[J].數(shù)學(xué)教育學(xué)報,2010(5):36-39. [4] 張奠宙,竺仕芬,林永偉.“數(shù)學(xué)基本活動經(jīng)驗”的界定與分類[J].數(shù)學(xué)通報,2008(5):4-7. [5] 蒙臺梭利.蒙臺梭利幼兒教育科學(xué)方法[M].任代文,譯.北京:人民教育出版社,2001. 收文日期:2017-09-27; 2017-10-28 鄭 良(1980-),男,安徽靈璧人,中學(xué)高級教師.研究方向:數(shù)學(xué)教育. O122 A 1003-6407(2018)03-0009-05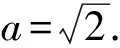
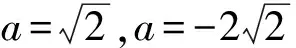
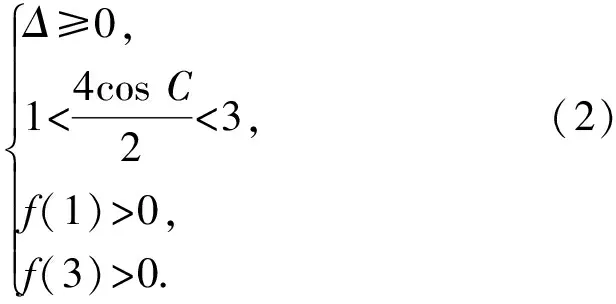
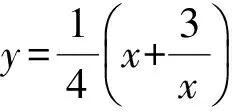
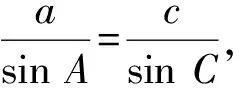
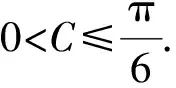
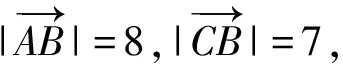
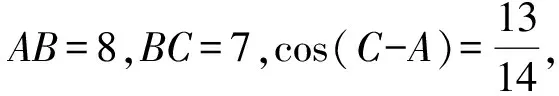
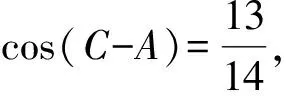
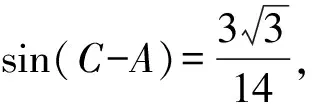
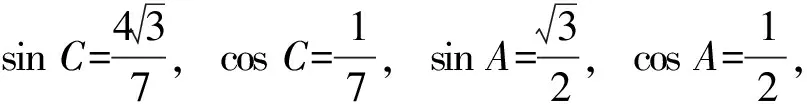
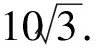
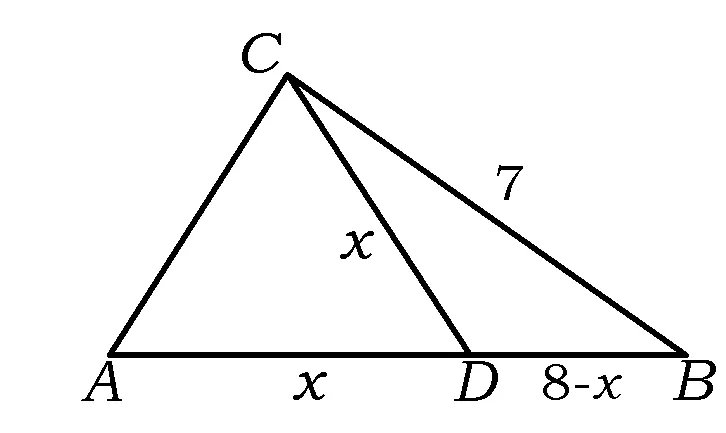
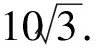
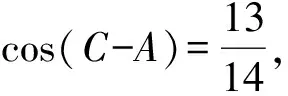
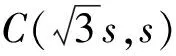
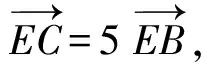

3 教學(xué)思考
3.1 深化“三個理解”,奠定教學(xué)基礎(chǔ)
3.2 強(qiáng)化數(shù)學(xué)探究,體驗數(shù)學(xué)發(fā)現(xiàn)
3.3 回歸數(shù)學(xué)理性,追求優(yōu)化創(chuàng)新

