氣柱共振對開洞結構內壓風洞試驗的影響

余先鋒， 謝壯寧， 劉海明， 張 承， 王 旭， 董 銳

(1. 招商局重慶交通科研設計院有限公司 橋梁工程結構動力學國家重點實驗室，重慶 400067；2. 華南理工大學 亞熱帶建筑科學國家重點實驗室，廣州 510640；3. 深圳市橋博設計研究院有限公司，廣東 深圳 518052)

與外壓相比，開洞結構風致內壓的一個最大特點就是氣流會在洞口處來回振動，這個氣流振動的特征頻率即為Helmholtz共振頻率。Helmhotlz共振的發生會直接提高內壓的峰值響應，在內外壓的聯合作用下，屋面板、門窗等圍護結構極易發生破壞[1-2]。

在風洞試驗中，若要正確模擬開洞結構的風致內壓，必須保證Helmholtz共振頻率得到正確模擬。Holmes[3]首次引入Helmholtz共振器模型來研究風致內壓，并指出模型內部體積必須按原型與實驗風速比的平方進行放大才能保證脈動內壓的正確模擬。余世策等[4]在對封閉式大跨屋蓋氣彈模型研究時，強調結構內部容積必須在模型自身容積的基礎上按風速比的平方進行放大，才能保證氣承剛度的相似模擬。Sharma等[5]從開洞建筑模型與原型的阻尼相似出發，亦導出了與Holmes相似的結論；他們進一步通過風洞試驗對比研究了2種相同補償體積但補償箱形狀不同(“深且窄”與“淺且寬”)時的內壓功率譜特性，結果表明補償箱形狀對風致內壓特性具有顯著的影響，“深且窄”的體積補償效果最好，它能保證脈動內壓的精確模擬，但“淺且寬”的體積補償箱會使得內壓功率譜上出現一個額外的共振峰，這與單腔內壓共振理論不符，試驗時不宜采用。

綜上可知，在進行開洞結構內壓風洞試驗時，不僅要保證模型內部體積按風速比的平方進行放大，還必須保證補償箱是“深且窄”的形狀，而非“淺且寬”的。值得注意的是，一般情況下，結構設計風速與實驗風速之比約為3∶1，對于單腔結構，補償后的體積為原結構容積的9倍，由于補償體積所形成的管道長度依然較小，此時氣柱共振頻率位于內壓功率譜的高頻區，對脈動內壓均方根的影響可忽略不計，但對于雙腔或多腔結構，體形補償箱形成的管道長度加倍，氣柱共振對脈動內壓的影響則較為顯著，必須在內壓信號處理時，通過濾波等手段消除氣柱管道共振的影響。

文中首先闡述開洞雙腔結構內壓風洞試驗的相似定律以及氣柱共振機理，然后通過開洞結構的多參數對比風洞試驗驗證氣柱共振現象的存在以及它對風致內壓特性的影響。

1 內壓風洞試驗相似定律及體積補償要求

對于圖1所示的兩空間結構，余先鋒等[6]導出其風致內壓響應的非線性控制方程組，如式(1)，(2)所示。

圖1 兩空間結構風致內壓模型Fig.1 Model of internal pressures for a two-compartment building

(1)

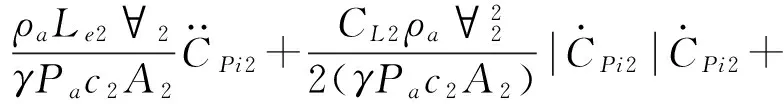
(2)

為保持試驗模型與結構原型之間的內壓動力響應相似性及正確獲得試驗模型的Helmholtz共振頻率，徐海巍等[7]對上述內壓控制方程組進行相似理論分析，得到兩空間結構內壓模型風洞試驗應滿足的條件為：

(3)

對于單空間結構內壓模型試驗，式(3)即簡化為：

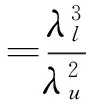
(4)

式中：λ?1、λ?2分別為子空間1、2的模型與原型之間的體積縮尺比，λl和λu分別為模型與原型的長度與風速縮尺比。由此可見，無論是單空間還是雙空間結構，在進行內壓風洞試驗時，模型的內部體積必須按設計風速與實驗風速比的平方進行放大補償。

值得注意的是，Sharma指出在進行開洞結構內壓風洞試驗時，體積補償箱必須是“深且窄”的[5]，見圖2(a)，而不宜采用圖2(b)所示的“淺且寬”的補償方式。他給出了不同體積補償方式下的內壓功率譜，見圖3，由圖可知：若不進行體積補償，所測得的Helmholtz共振頻率會被顯著放大；若采用淺且寬的體積補償方式，所測得的內壓功率譜上會出現兩個共振峰，而采用深且窄的補償方式，則所得的內壓功率譜是正確的，且Helmholtz共振頻率與理論值吻合良好。

圖2 體積補償箱的放置方式Fig.2 Additional cavities to effect volume distortion

圖3 不同體積補償方式下的內壓功率譜[5]Fig.3 Internal pressure spectra versus frequency for different additional cavities

2 氣柱共振頻率的計算

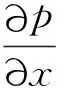
(5)

采用牛頓第二定律對流體微團進行受力分析，可得運動方程為：

(6)

圖4 等截面直管道中的流體微團受力分析Fig.4 Force analysis for the fluid in a prismatic and straight pipe

由式(5)，(6)可得經典的平面波動方程[8]為：

(7)

式中：a為聲速；ρ為流體密度。采用分離變量法可得式(7)的理論解為：

(8)

將式(8)代入式(6)，可得：

(9)

式中：ω為脈動圓頻率；A，B為復數常數，可由管道的邊界條件確定。

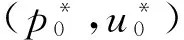
(10)

對于一端封閉、一端開啟的等截面直管道，管道長度為l，據封閉端的邊界條件(速度為0，壓力不為0)及開啟端的邊界條件(速度不為0，壓力為0)，可得管道的氣柱固有頻率方程為：

(11)

(12)

式(12)即為等截面直管道的氣柱共振基頻的計算公式，式中a為聲速，取為340 m/s，l為管道長度。

3 內壓風洞試驗驗證

上文指出，為保證試驗模型與結構原型之間的內壓動力響應相似性以及正確模擬結構的Helmholtz共振頻率，試驗模型內部體積必須按設計與實驗風速比的平方進行放大，且體積補償箱必須是“深且窄”的。然而，當體積補償箱形成的管道過于深長時，則會出現氣柱共振現象而導致內壓測量結果不準。

3.1 風洞試驗概況

為驗證氣柱共振現象的存在并分析其對內壓響應的影響，下文對一開洞兩空間結構進行了內壓風洞試驗。試驗模型按 TTU(Texas Tech University)實測房以1∶25縮尺并采用5 mm有機玻璃板制作而成，試驗模型尺寸(長×寬×高)為548 mm×364 mm×160 mm，隔墻位于模型長度方向的中央，使得兩子空間的體積均占總體積的50%，模型迎風墻面中央共有4種開洞尺寸，分別為110 mm×110 mm，80 mm×80 mm，60 mm×60 mm，40 mm×40 mm；沿模型長度方向設置一隔墻，在隔墻中央開有一方孔，尺寸為40 mm×40 mm。在兩個子空間的內墻面上各布置了2個內壓測點。

模型測壓試驗是在華南理工大學風洞試驗室進行的，大氣邊界層流場按建筑結構荷載規范(GB50009—2012)模擬了B類地貌風場，模擬的平均風速、湍流度剖面見圖5。

風洞試驗中皮托管高度40 cm(對應原型10 m)處的平均參考風速為10 m/s，假定原型結構的設計風速為30 m/s，故風速比為3∶1，則據式(3)所示的相似律要求，補償后的總體積須為原體積的9倍，而且補償箱必須是“深且窄”的。為作比較，文中還制作了一個相同的試驗模型，但補償后總體積為原體積的2倍。不同體積補償后的內壓試驗模型見圖6，其中模型1、2補償后總體積分別為原體積的2倍和9倍。試驗采樣頻率為331 Hz，采樣時間為61.8 s。

圖5 模擬的B類風場特性Fig.5 Simulated velocity profile and turbulence profile in the wind tunnel

圖6 不同體積補償后的內壓試驗模型Fig.6 Internal pressure experimental models for different additional cavities

3.2 試驗結果分析

對于模型1，補償后的總體積是原體積的2倍，當其隔墻開洞尺寸為40 mm×40 mm時，不同迎風墻面開洞面積下的兩子空間內壓系數功率譜如圖7所示。從圖中可知：①不同開洞面積下的內壓系數功率譜圖中均出現兩個共振峰值，分別對應于開洞兩空間結構的兩個Helmholtz共振頻率。②當迎風墻面開洞面積較大時(如圖7(a)，7(b))，內側子空間2的低頻共振峰能量明顯高于外側子空間1，但子空間2的高頻共振峰能量卻低于子空間1，這與文獻[9]的結論是一致的。③隨著迎風開洞面積的減小，子空間2的低頻共振峰能量呈減弱趨勢，但子空間2的高頻共振峰值能量卻呈增大趨勢。

對于模型2，補償后的總體積是原體積的9倍，當其隔墻開洞尺寸為40 mm×40 mm時，不同迎風墻面開洞面積下的兩子空間內壓系數功率譜如圖8所示。從圖中可以看出：①不同開洞面積下的內功系數功率譜上除了出現兩階Helmholtz共振峰之外，還出現了氣柱共振峰值，三種迎風墻面開洞面積下的氣柱共振頻率約為30～32 Hz，這與由式(12)求得的氣柱共振頻率理論解f1=a/(4l)=30.4 Hz基本吻合，式中a為速340 m/s，l為氣柱長度，文中l為2倍的補償箱高度，即2.8 m。②各種迎風開洞面積下，內側子空間2的低頻Helmholtz共振峰能量依然高于外側子空間1，但子空間2的高頻Helmholtz共振峰能量卻低于子空間1。③由于外側子空間1直接受迎風開洞外壓激勵，其氣柱共振現象明顯，但內側子空間2僅受隔墻開洞氣流的激勵，由于激勵源較弱，其氣柱共振頻率及第2階Helmholtz共振頻率均不明顯。

圖7 不同開洞面積下的內壓系數功率譜(2倍體積補償)Fig.7 Internal pressure spectrum for different dominant opening areas in model 1

圖8 不同開洞面積下的內壓系數功率譜(9倍體積)Fig.8 Internal pressure spectrum for different dominant opening areas in model 2

對比分析模型1和2可知，補償后的模型1總體積為原體積的2倍，風速比僅為1∶1.41，由于實驗參考風速約為10 m/s，按風速比換算得到原型結構設的計風速約為14 m/s，對應50年重現期基本風壓約為0.12 kPa，遠低于大部分地區的基本風壓值。而對于模型2，由于補償后的總體積為原體積9倍，風速比達到3∶1，換算后的原型結構設計風速為30 m/s，對應的50年重現期基本風壓約為0.6 kPa，此時的試驗結果對大部分地區的開洞結構抗風設計均有參考價值，因此補償體積8倍(總體積9倍)使得風速比達到3∶1，此時測得的風致內壓是合理的且具有參考價值。然而，依據體積補償箱必須是“深且窄”的原則進行模型內部容積補償，則會出現氣柱共振現象，從而使得脈動內壓出現畸變，這與實際情況不符。為此，在進行開洞結構內壓風洞試驗時，首先要確定合理的風速比，并按風速比的平方進行體積放大補償；其次，體積補償箱必須是“深且窄”的；最后，補償箱不宜過于深長(一般出現于連通的兩空間或多空間結構)，以免出現氣柱共振現象而給試驗結果帶來誤差。

4 結 論

本文通過開洞結構的多參數對比風洞試驗驗證了氣柱共振現象的存在，并分析了它對風致內壓特性的影響。主要結論如下：

(1)在進行內壓風洞試驗時，首先要確定合理的風速比，使得換算后的原型結構設計風壓可覆蓋大部分地區的基本風壓值。

(2)實驗時，必須按結構設計風速與實驗風速比值的平方進行模型體積補償，且體積補償箱須遵守“深且窄”的原則。

(3)對于連通的兩空間或多空間結構，可通過式(12)估算一階氣柱共振頻率，另外補償體積箱不宜過于深長，以免出現氣柱共振現象而影響內壓的測量結果。

[ 1 ] 黃鵬, 陶玲, 全涌, 等. 浙江省沿海地區農村房屋抗風情況調研[J]. 災害學, 2010, 25(4): 90-95.

HUANG Peng, TAO Ling, QUAN Yong, et al. Inverstigation of wind resistance performance of rural houses in coastal area of Zhejiang province [J]. Journal of Catastrophology, 2010, 25(4): 90-95.

[ 2 ] 李壽科, 田玉基, 李壽英, 等. 屋蓋開孔建筑的內壓風洞試驗研究[J]. 振動與沖擊， 2016, 35(18): 1-8.

LI Shouke, TIAN Yuji, LI Shouying, et al. Wind tunnel tests on internal pressures of buildings with a roof opening [J]. Journal of Vibration and Shock, 2016, 35(18): 1-8.

[ 3 ] HOLMES J D. Mean and fluctuating internal pressures induced by wind [C]. Proceedings of the 5th International Conference on Wind Engineering, Colorado State University, 1979.

[ 4 ] 余世策, 孫炳楠, 樓文娟. 封閉式大跨屋蓋氣彈模型風洞試驗的氣承剛度模擬[J]. 浙江大學學報(工學版), 2005, 39(1): 6-10.

YU Shice, SUN Bingnan, LOU Wenjuan. Pneumatic stiffness simulation of wind tunnel aeroelastic model tests for closed long-span roof [J]. Journal of Zhejiang University (Engineering Science), 2005, 39(1): 6-10.

[ 5 ] SHARMA R N, MASON S, DRIVER P. Scaling methods for wind tunnel modelling of building internal pressures induced through openings [J]. Wind and Structures, 2010, 13(4): 363-374.

[ 6 ] 余先鋒, 全涌, 顧明. 開孔兩空間結構的風致內壓響應研究[J]. 空氣動力學學報, 2013, 31(2): 151-155.

YU Xianfeng, QUAN Yong, GU Ming. Study on responses of wind-induced internal pressure in a two-compartment building with a dominant opening [J]. Acta Aerodynamica Sinica, 2013, 31(2): 151-155.

[ 7 ] 徐海巍, 余世策, 樓文娟. 開孔雙空腔結構風致內壓動力特性的研究[J]. 工程力學, 2013, 30(12): 154-159.

XU Haiwei, YU Shice, LOU Wenjuan. Study on wind induced internal pressure dynamic characteristic for an opening structure with two compartments [J]. Engineering Mechanics, 2013, 30(12): 154-159.

[ 8 ] 黨錫淇, 陳守五. 活塞式壓縮機氣流脈動與管道振動[M]. 西安: 西安交通大學出版社, 1984.

[ 9 ] SHARMA R N. Internal pressure dynamics with internal partitioning [C]. Proceeding of the 11th International Conference on Wind Engineering, Lubbock Texas, 2003.