淺談高考中離心率問題的三大題型
■福建省龍巖市永定區城關中學 童其林(特級教師)
求圓錐曲線的離心率或取值范圍問題是一類較為常見的問題,也經常出現在歷年高考試題中。不少同學在處理離心率的取值范圍問題時,常常無從下手,不知道確定參數范圍的函數關系或不等關系從何而來。下面通過一些實例介紹圓錐曲線的離心率的求法,及離心率取值范圍問題形成的幾個背景及相應的解法,期望對同學們有所幫助。
一、求離心率的值
關鍵是找到含有a、b、c的一個等式,可借助圖形、圓錐曲線定義或常見結論等知識尋求解決問題的突破口。

圖1
點評:(1)畫圖很重要,要做對題,最好先畫圖。(2)此題圖形有點復雜,關鍵是要找到關于a、b、c的一個等式,需要沉著冷靜,膽大心細。

圖2
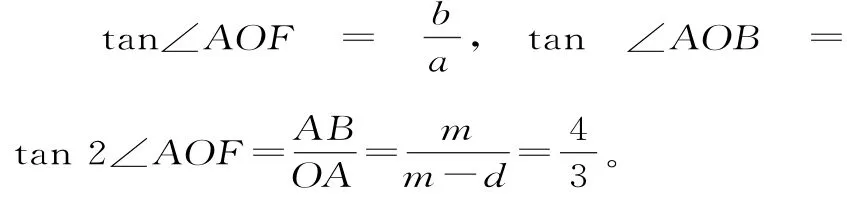
點評:求離心率有很多種方法,對本題而言,利用角度的關系,可快速溝通知識模塊之間的聯系。
已知F1、F2是雙曲線1(a>0,b>0)的左、右焦點,若雙曲線左支上存在一點P與點F2關于直線y=對稱,
則該雙曲線的離心率為____。

點評:雖然思路明確,但運算量較大。
解法2:因為點P與點F2關于直線y=對稱,所以FP被直2x垂直平分,交于A點。如圖3,可得t a nθ+|O A|2=c2,解得|A F2|=b,|O A|=a。
圖3
又O A為△F2P F1的中位線,所以|P F1|=2|O A|=2a,|P F2|=2|A F2|=2b。
由雙曲線定義可得|P F2|-|P F1|=2a,所以2b-2a=2a,b=2a,故b2=4a2。因此,c2-a2=4a2,c2=5a2

圖4
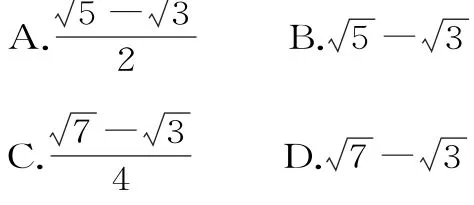
如圖4,圓O的方程為x2+y2=a2,設P點坐標為(x0,y0),則圓O的切線P F2的方程為x0x+y0y=a2。又切線過點F2(c,0),所以
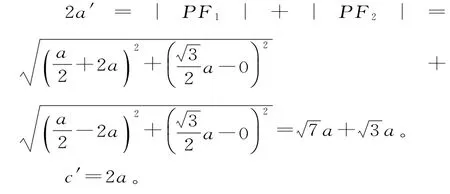
二、求離心率的范圍或最值
1.利用題目所給的條件
利用題設條件能溝通所求參數與曲線上點的坐標或曲線的特征參數之間的聯系,建立不等式或不等式組求解。
·kMA2
<2,則雙曲線C的離心率的取值范圍為( )。
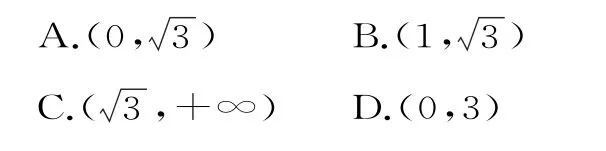
解析:由題設知A1(-a,0),A2(a,0)。假設M點坐標為(x,y),當點M在x軸上時,滿足kMA1·kMA2
<2。
當點M不在x軸上時,滿足:

2.利用已知變量的范圍
利用題中給出的某個已知變量的范圍,或由已知條件求出某個變量的范圍,然后找出這個變量與欲求的參變量之間的關系,進而求解。

解析:如圖5,因為B 和A 關于原點對稱,,所以點B 也在橢圓上。

圖5
O是R t△A B F的斜邊中點,且|O F|=c,故|A B|=2c。
又|A F|=2cs i nα,②|B F|=2cc o sα,③
把②③代入①,得2cs i nα+2cc o sα=2a。


點評:本題把橢圓的定義、幾何性質、解三角形,以及三角恒等變換都派上了用場,可見完成一個較復雜問題的解答過程需要全方位的知識運用。
3.利用曲線自身的取值范圍
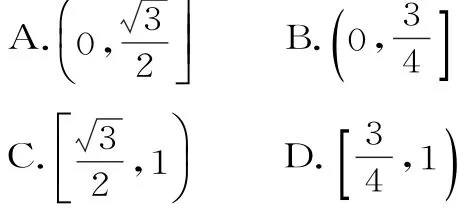
解析:如圖6,設橢圓的左焦點為F1,半焦距為c,連接A F1,B F1,則四邊形A F1B F為平行四邊形,所以|A F1|+|B F1|=|A F|+|B F|=4。

圖6
根據橢圓定義知:
|A F1|+|A F|+|B F1|+|B F|=4a。所以4a=8,a=2。因為點M到直線l的距離不小于所以橢圓的離心率的取值范圍為
點評:此題重點考查同學們的等價轉化與化歸的能力,由|A F|+|B F|=4需要推出|A F|+|A F1|=2a,另一方面要重視圖形對解題的引領作用。
4.利用二次方程有解的前提條件
判斷直線和圓錐曲線的關系是解析幾何中最常見的題型,它們聯立消元后所得的判別式為非負值是直線和圓錐曲線有公共點的充要條件。若有限制條件,則還應考慮根的分布情況,這是確定參數取值范圍的一個常見條件。

解析:設點F2坐標為(c,0)。由于F2關于直線P F1的對稱點M恰在y軸上,不妨設M在正半軸上,由對稱性可得,|MF1|=|F1F2|=2c,且|MF1|=|MF2|,故∠MF1F2=6 0°,∠P F1F2=3 0°。
1入雙曲線方程得:
(3b2-a2)x2-2c a2x-a2c2-3a2b2=0。
因為方程有兩個異號的實數根,所以3b2
點評:取值范圍問題,要尋找滿足題設的不等式,不等式從何而來?要結合圖形分析,要挖掘隱含條件。由于本題的直線P F1與雙曲線恒有兩個交點,這兩個交點在原點的兩邊,即關于x的二次方程的兩個根一正一負,所以只需滿足兩根之積小于0,問題便得以解決。
5.利用圖形的位置關系

三、與離心率交匯的其他問題
對這類問題要注意全方位、多角度地去思考,尋求多種途徑,盡可能通過分析推理得出最簡便的方法。

解法1:如圖7,設|P F1|=r1,|P F2|=r2(r1>r2),|F1F2|=2c,橢圓的長半軸長為a1,雙曲線的實半軸長為a2,橢圓、雙曲線的離心率分別為e1、e2。
由余弦定理得:

解法2:如圖7,設|P F1|=r1,|P F2|=r2(r1>r2),|F1F2|=2c,橢圓的長半軸長為a1,雙曲線的實半軸長為a2,橢圓、雙曲線的離心率分別為e1、e2。



圖7
解法3:如圖7,設|P F1|=r1,|P F2|=r2(r1>r2),|F1F2|=2c,橢圓的長半軸長為a1,雙曲線的實半軸長為a2,橢圓、雙曲線的離心率分別為e1、e2。
由余弦定理得4c2=r21+r22-r1r2=(r1+r2)2-3r1r2=4a21-3r1r2,所以e12=
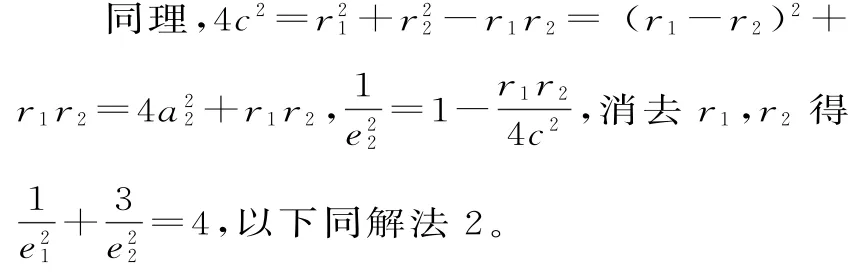
解法4:如圖7,設|P F1|=r1,|P F2|=r2(r1>r2),|F1F2|=2c,橢圓的長半軸長為a1,雙曲線的實半軸長為a2,橢圓、雙曲線的離心率分別為e1、e2。
解法5:如圖7,設|P F1|=r1,|P F2|=r2(r1>r2),|F1F2|=2c,橢圓的長半軸長為a1,短半軸長為b1;雙曲線的實半軸長為a2,虛半軸長為b2,橢圓、雙曲線的離心率分別為e1、e2。
點評:以“形”入手,借助函數、柯西不等式、三角函數、焦點三角形面積公式等,都是為了有效地架起已知與求解之間的橋梁,意在考查同學們利用知識,等價轉化問題,解決問題的能力。
總之,求圓錐曲線的離心率及取值范圍要抓住一個關鍵,兩個切入點,三個方向,四種工具,五種思想。
一個關鍵:尋找,尋求建立a、b、c(或a、b、c中的兩個)的一個等式或不等式;
兩個切入點:從“形”入手,從“數”下手;
三個方向:從圓錐曲線的定義思考,從幾何圖形的性質出發,從方程(或不等式)的角度落筆;
四種工具:平面幾何基礎知識,平面向量的知識,三角函數的運用,柯西不等式;
五種思想:數形結合的思想,方程思想,函數思想,等價轉化思想,分類討論思想。
(責任編輯 徐利杰)

