多點同步內爆炸下典型艙室的毀傷特性

2018-02-10 02:44:18翟紅波李芝絨蘇健軍張玉磊姬建榮

振動與沖擊 2018年2期

關鍵詞：變形

翟紅波，李芝絨，蘇健軍，張玉磊，姬建榮

(西安近代化學研究所，西安 710065)

多點起爆、多個彈藥同時爆炸是作戰使用中的一種常見現象[1]。炸藥點起爆后，產生的沖擊波將以起爆點為中心以球面波形式傳播，同時起爆兩個不同位置處的裝藥，形成的兩個球面波在一定時間后將相遇并相互疊加[2-3]。一定情況下的沖擊波相互疊加可使作用區域內的壓力顯著增強，有助于提高彈藥的爆炸威力，增強對目標的破壞能力[4]。因此，研究多點爆炸下的沖擊波性能對于彈藥設計和毀傷評估具有重要的應用價值。

近年來，眾多學者圍繞彈藥多點聚集爆炸效應開展了廣泛深入的研究。陳志林[5]研究了空氣中的兩點聚集爆炸，發現在裝藥當量相同時，多點聚集爆炸沖擊波的地面破壞殺傷范圍大于單點爆炸。林大超等[6]通過實驗研究了地面附近爆炸時地面豎向振動幅值特性并得到了地面豎向振動速度，國勝兵等[7]基于爆炸地震波的非平穩隨機過程模型，建立了兩點和多點(微差)爆炸地震波實用模擬方法，模擬多點爆炸后形成的復合地震效應。顧文彬等[8]對淺層水中沉底爆炸沖擊波相互作用數值模擬進行了研究，研究發現沖擊波相互作用的疊加或多次沖擊作用大大提高了爆炸威力。李旭東等[9]研究了三點同時爆炸時沖擊波在水泥砂漿板中聚集效應的特點和規律，結果表明，由于聚集效應的影響，正應變在聚集區域內發生強烈的非線性激增，并且在距離爆炸點更長的距離內維持高應力狀態。張世豪等[10]分別從爆炸應力波和爆炸能量角度研究了多點爆炸能量聚集效應，結果表明，多點爆炸應力波在裝藥對稱位置發生相互作用壓力疊加，造成混凝土變性能密度及內能密度較單點爆炸時顯著下降，從而導致多點起爆毀傷區域較單點爆炸時增大。胡宏偉等[11]研究了多點同步地面爆炸沖擊波的相互作用，計算了沖擊波相互疊加區域的壓力和沖量，研究發現多個裝藥同步爆炸時，沖擊波超壓和沖量都顯著增加，大大提高了裝藥爆炸威力。王龍侃等[12]研究了水下爆炸作用對加筋板架結構的毀傷效應，分析了加筋板架結構的破壞模式。

盡管多點聚集爆炸領域取得了很多研究成果，但多是針對爆炸效應的研究，較少涉及內爆炸環境下多點爆炸的耦合效應，關注船艙毀傷效果的研究更少。因此，研究內爆炸環境多點同步內爆炸的爆炸效應特征，為多點同步內爆炸的深入研究提供基礎，具有重要的學術價值。本文基于某艦船艙室的1∶8等效縮比模型，通過雙點裝藥同步內爆炸試驗，對比分析雙點裝藥同步內爆炸和單點裝藥內爆炸的爆炸效應特征，研究兩種條件對艙室的毀傷效果。

1 試驗設計

由于實裝目標爆炸試驗存在成本高、周期長等不足，縮比模型試驗是一個較為常用的替代方案。縮比模型設計，采用幾何統一縮比的方法，即艙室的幾何尺寸(長、寬、高、壁厚)采用相同的比例進行縮比，這帶來兩個問題：①原型艙室結構材料較難獲取；②艙壁厚度縮比后，厚度很小，既降低艙壁剛度，又增大了加工難度。因此，引入強度等效原則，在模型艙室中采用較厚的低強度鋼代替原型艙室的高強度鋼，使其結構強度一致，同時可增強艙壁整體剛度，提高其與原型艙室毀傷效應的一致性。對某艦典型艙室進行縮比，設計了縮比比例為1∶8的縮比艙室，如圖1所示。模型幾何尺寸如表1所示。

圖1 艙室結構模型Fig.1 The model of some ship cabin

表1 模型的幾何尺寸

為了分析多裝藥在艙室內爆炸的作用特點和對艙室的毀傷效果，設計兩組試驗條件，一是在艙室幾何中心處懸掛30 g藥柱，二是在幾何中心兩側0.22 m分別懸掛兩個15 g藥柱并同時起爆，如表2所示。

表2 試驗條件

試驗炸藥為TNT藥柱，密度1.58 g/cm3，如圖2所示。傳爆藥柱為JH-14炸藥，藥量為5 g，尺寸為φ15×17，用于起爆TNT裝藥，起爆雷管選用8號電雷管。

圖2 試驗用炸藥和傳爆藥柱Fig.2 The charge and the booster charge of the test

試驗包含兩種條件：A，縮比艙室單點內爆炸；B，縮比艙室雙點內爆炸。其試驗方案如下所述：

條件A：將典型艙室模型放置在平坦地面上，試驗藥柱垂直懸掛于爆炸艙室內部的幾何中心，在模型壁面上安裝壓力傳感器測量內爆炸沖擊波波形(見圖3)。在距離爆心安全距離100 m外正交2個方向上布置高速動態分析儀(見圖4)，觀察內爆炸作用下模型的實時變化狀態。爆炸結束后觀察模型變化情況并記錄試驗數據。試驗裝置布局示意圖如圖5所示。

條件B：試驗布置同條件A，將單點爆炸藥量的1/2(15 g)作為多點內爆炸藥量，將兩藥柱分別懸掛于距離單點爆心0.22 m處，二點連線為艙室中線，艙室模型試驗藥量依次為2×15 g，爆炸結束后觀察并記錄艙壁破壞情況，與單點內爆炸破壞情況對比分析。

圖3 艙室Fig.3 The cabin

圖4 高速動態分析儀Fig.4 High speed dynamic analyzer

圖5 試驗裝置現場布局Fig.5 Field layout of the test

2 雙點同步內爆炸載荷特征簡要分析

炸藥在空氣中爆炸時，沖擊波以球對稱狀向外傳播。當沖擊波與壁面相碰時，產生了沖擊波的壁面反射。通常，沖擊波壁面反射可以分為規則反射、過渡反射、非規則反射和半球反射四種[13]。

當入射沖擊波的入射角超過一個臨界角(取決于沖擊波強度)后，反射波陣面和反射波陣面的交點會離開地面，二者合成第三個沖擊波，即馬赫波。這個交點也被稱作“三波點”，交點的下面為馬赫桿波陣面，它的底部垂直于壁面。三波點的位置和馬赫桿的高度隨時間和距離而變，相應的三波點軌跡是一條上凹的曲線，如圖6所示。實際上，馬赫桿并不是均勻的平面沖擊波，而是帶有某種輕微彎曲的波[14]。

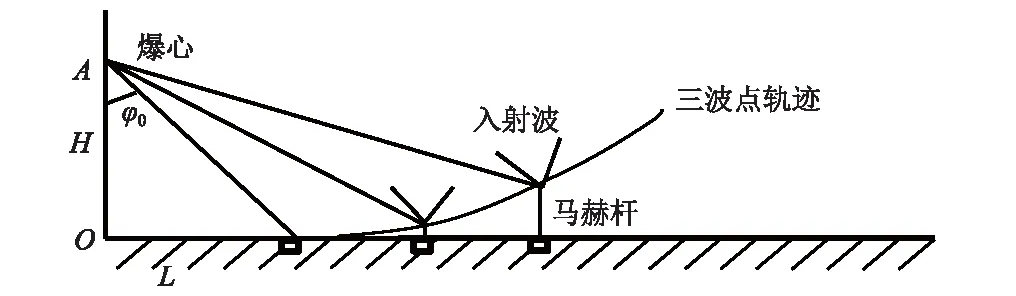
圖6 馬赫波示意圖Fig.6 The sketch map of Mach wave

在該艙室模型中，爆心高度H=0.175 m。

對于條件A，等效TNT裝藥ω=0.03 kg，有

由此，可根據計算公式得到馬赫反射臨界角φ0c=40°。以B2點為例，φ0=arctan(0.55/0.175)=72.4°，顯然φ0>φ0c，因此B2點處的沖擊波超壓屬于馬赫反射。

對于條件B，等效TNT裝藥ω=0.015kg，有

由此，可根據計算公式得到馬赫反射臨界角φ0c=39.2°。B2點，φ0=arctan(0.59/0.175)=73.5°，顯然φ0>φ0c，因此B2點處的沖擊波超壓屬于馬赫反射。

在船艙模型中，需要關注的是側艙壁(代表實船的橫隔壁與側舷)的毀傷，B2點即處于側艙壁的中心區域。通過分析發現，在A、B兩種條件下，B2點均處于馬赫反射區內。在B條件下，雙點裝藥的同步爆炸會在B2點附近形成疊加沖擊波，加入雙點起爆的同步性很好，相位差小于沖擊波正壓作用時間，那么B2點處沖擊波峰值和沖量都會出現疊加增大；否則，B2處的超壓峰值變化不大，但沖擊波沖量會有疊加增大。

爆炸沖擊波毀傷船艙目標結構時，一般來說有三種毀傷準則：①當t2T時，適用峰值準則；③在上述二者之間時，適用峰值-沖量準則。其中，T為艙室結構的自振周期，t為沖擊波作用的脈寬。艙壁結構的一階自振頻率一般均小于50 Hz，即自振周期一般大于20 ms，而艙室內爆炸屬于中近場作用，沖擊波的作用脈寬在1 ms左右，遠小于自振周期的1/5，因此艙壁的沖擊波毀傷一般符合沖量準則。雙點裝藥同步爆炸可增大中心面處的沖量，有效提高對艙室的毀傷效果。

3 艙室變形

以起爆時刻為0時刻，通過高速錄像獲得艙室不同時刻的形態演變，圖7給出了條件B的爆炸實時分幅照片。從高速攝影觀察，2個條件艙室變形過程基本相同：t=0 ms時，炸藥起爆；t=3 ms時，艙室上表面中部開始出現鼓包，如(b)所示；此后，鼓包從上表面中部向邊緣擴散，高度逐漸降低，形成一個斜坡，整個上表面向外膨脹變形，到t=8 ms時，艙室上表面變形達到最大，如(c)所示；隨后，艙室上表面中部鼓突部分開始向里運動，大約經過4～5 ms時間，上表面又開始向外運動，在4～5 ms時間后，上表面再次向內運動，在此后的較長一段時間內，上表面呈現周期性振蕩，周期約為8～10 ms；在t=50 ms時，振蕩幅度開始減緩，最后上表面呈現中間鼓突的“四斜坡形”變形。

圖7 艙室變形過程(條件B雙點內爆試驗)Fig.7 The cabin deformation process (the double-point charge explosion test of working condition B)

內爆炸作用后，艙室四周壁面無明顯變形，上下壁面中間均出現了不同程度的鼓突，呈“四斜坡形”變形，如圖8所示。將起爆口所在側記為“前側”，對艙室上壁面各側變形進行測量，各側變形量如表3所示。

圖8 艙室變形Fig.8 The cabin deformation

進行的2種條件的艙室內爆試驗中，艙室均未破裂，四周壁面也沒出現明顯的變形，但是艙室上壁面出現了明顯的塑性變形，這主要原因可能是因為艙室高度比較低，爆轟產物和沖擊首先到達上下壁面，其中壁面中部是塑性變形最大的區域，從高速錄像可以看出，中部也是最開始出現變形的區域，到最后上壁面中部鼓突，呈現“四坡頂形”變形；從試驗結果可知，30 g藥量的艙室單點內爆試驗艙室上壁面平均變形量為22.5 mm，2×15 g藥量的艙室雙點內爆炸試驗艙室上壁面平均變形量為35.25 mm。由此可知，艙室內爆試驗中，裝藥量相同時，雙點爆炸艙室的變形量更大。從毀傷的角度出發，合適位置處的雙點爆炸更利于毀傷。

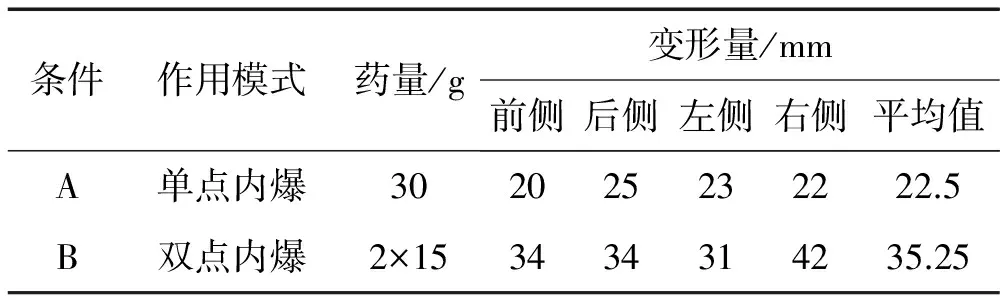
表3 艙室變形量

4 內爆炸壓力

壓力傳感器位于模型A、B、C面(圖8)，經過信號線連接至信號調理器與數據采集器，具體測點布局，如圖9所示。

圖9 艙室各面測點布局Fig.9 Layout of measurement points

由于密閉艙室內存在固壁反射，且各反射波會相互作用，因此實際的波形非常復雜。典型的壁面壓力曲線如圖10所示，讀取壓力曲線，獲得不同測點的超壓、沖量，如表4所示。圖10(a)的B2點在橫艙壁的中心處，超壓曲線存在兩個較高峰值，第一峰值為馬赫波的反射，第二峰值為其它壁面反射波和稀疏波的合成波；圖10(b)的C11點在艙內上甲板的角隅處，第一峰為馬赫波，第二峰值超過第一峰值，為合成馬赫反射波。

圖11是測點C21-C25(與雙點裝藥的軸線平行)在兩種條件下的沖擊波壓力峰值和沖量的對比圖。從圖中可以看出，條件A沖擊波峰值衰減很快，在艙室中心C24點峰值超壓約等于條件B的1.4倍，在C22點峰值小于條件B。對于沖量載荷，3 ms時間內，艙室幾何中心位置處的沖量條件A大于條件B。條件B的沖量呈現馬鞍形，雙點裝藥中心面上(C24點)的沖量最大，趨于角隅位置(C21點)沖量次之，中間位置沖量最小，沖量趨于勻化速度比較快。

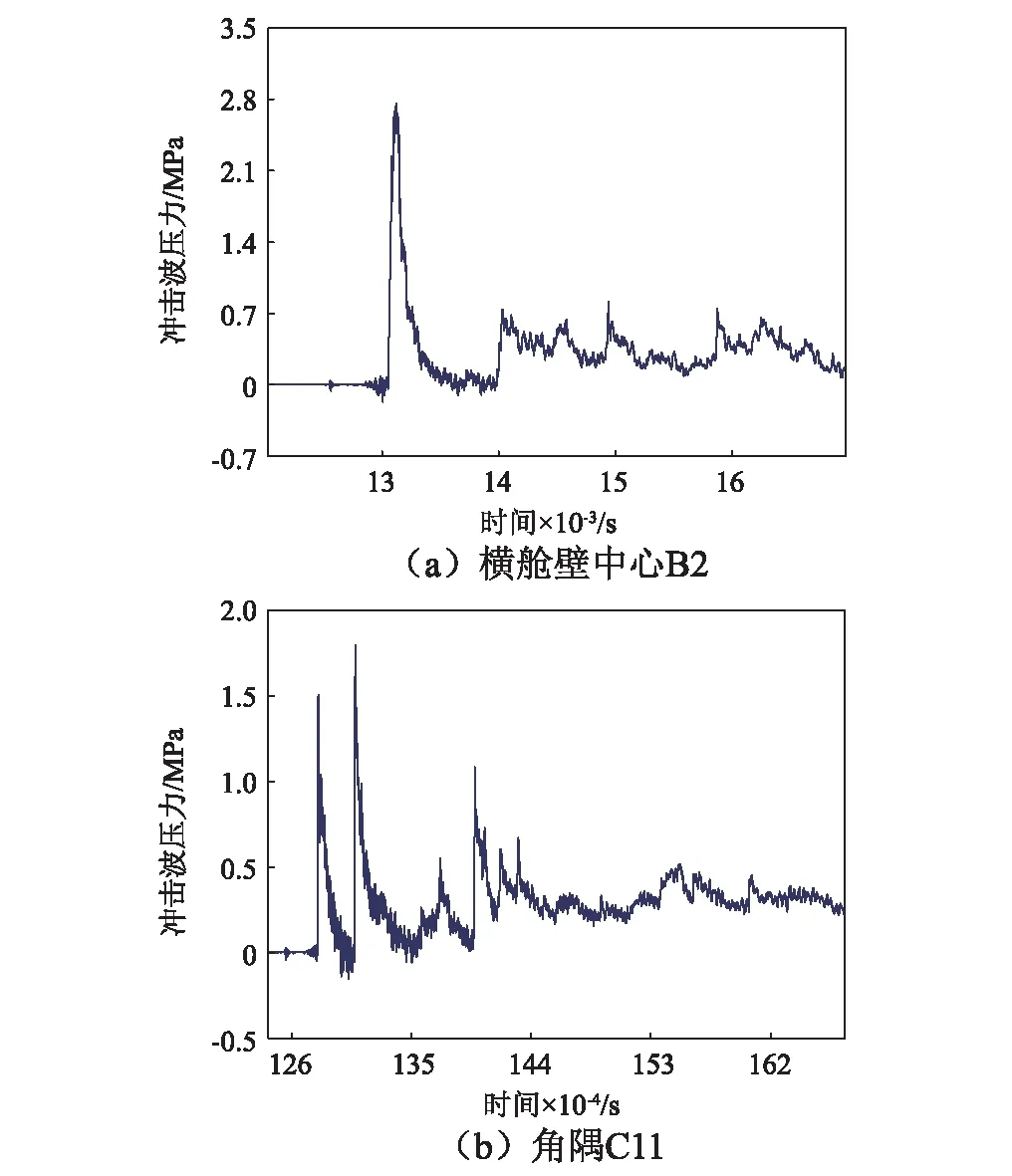
圖10 壓力曲線Fig.10 Pressure curve

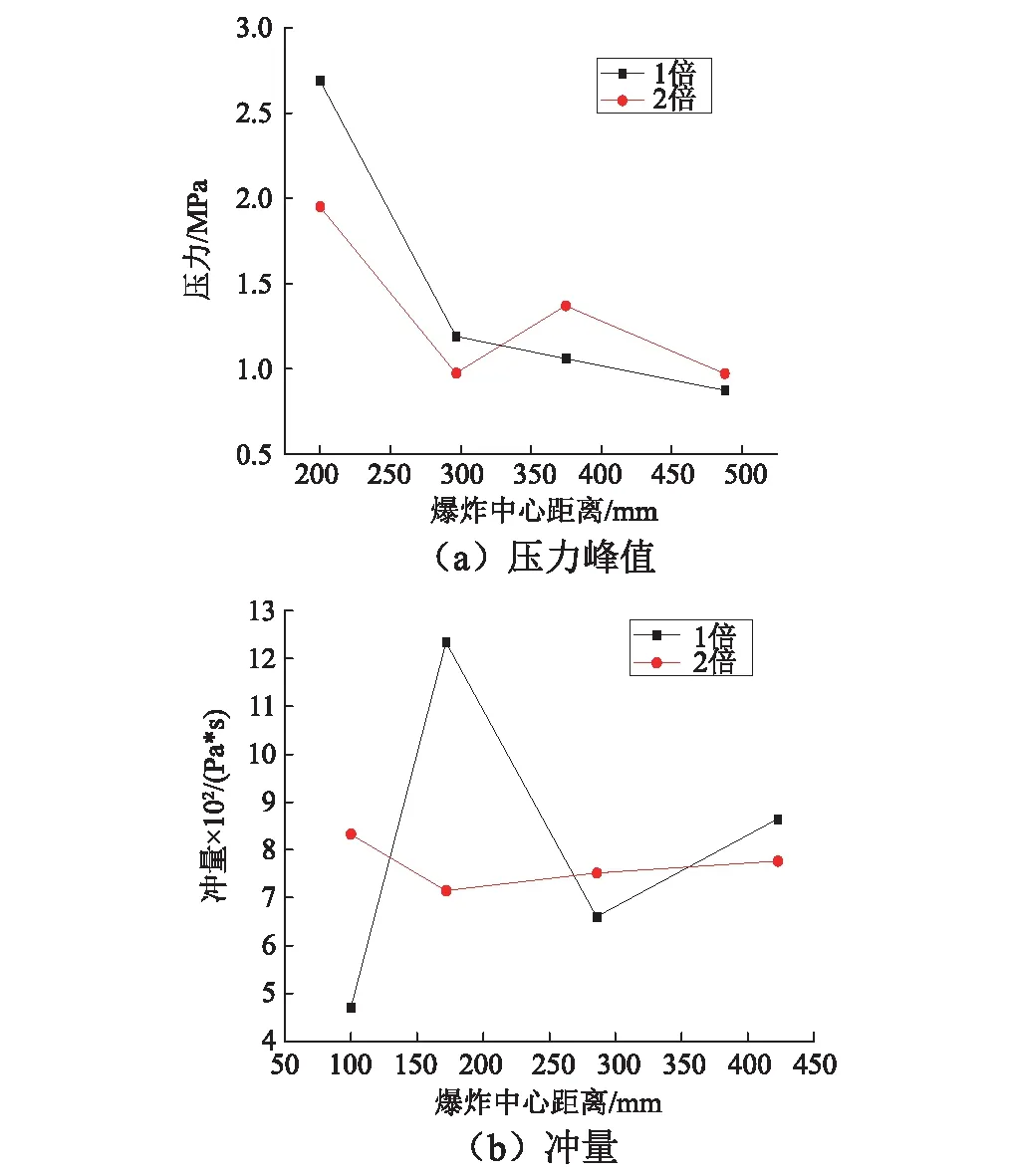
圖11 兩種條件下沖擊波壓力峰值和沖量對比Fig.11 Pressure peak and impulse with two working condition

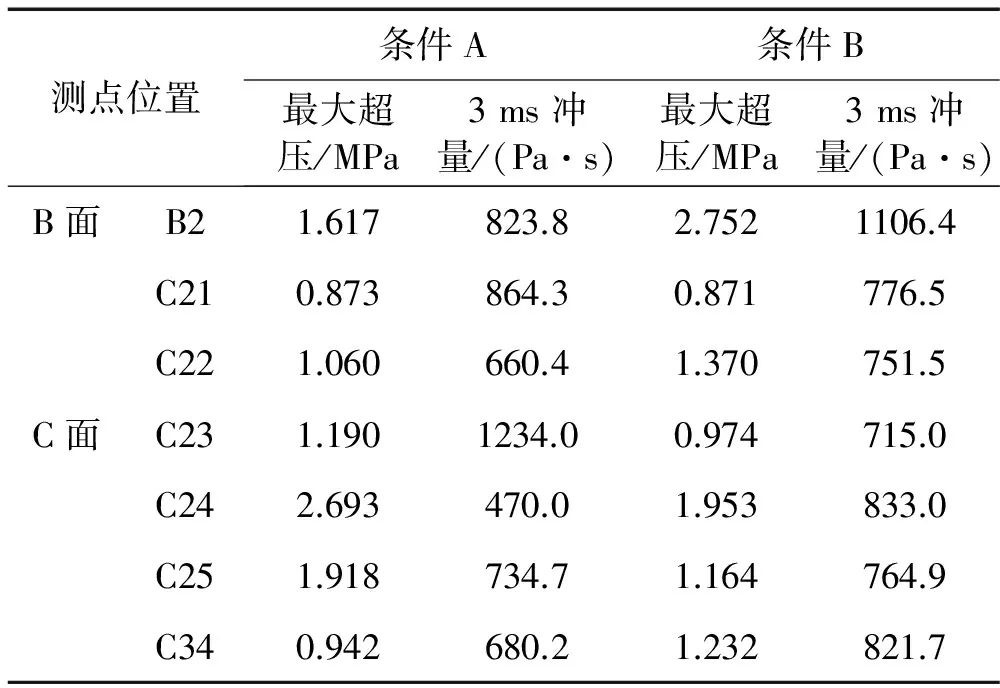
表4 艙室壓力測試數據

圖12給出了雙點中心面上B2和C34點(即雙點爆炸加強區)的沖量對比圖，表5給出了測點B2在兩種條件下的沖量對比。從中可以發現，橫隔壁和上下甲板的中心面上，同等藥量雙點爆炸比單點爆炸產生的沖量效應大，即在此部位產生爆炸沖量加強區。在3 ms時刻(該模型符合沖量準則的五分之一周期，此時的沖量對艙室毀傷有效)，條件B的沖量比單點爆炸大35.8%。說明對該種縮比艙室，雙點裝藥爆炸的毀傷效果比同等藥量單點爆炸要好。

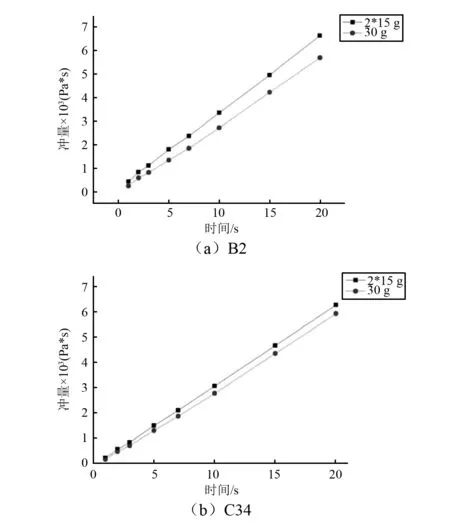
圖12 同等藥量兩種條件下沖量圖Fig.12 The impulse with two working condition

之所以造成這種狀況，是由于雙點裝藥同時起爆時，沖擊波同時到達雙點的中心面(B2和C34點)，并在其上形成疊加，疊加后的沖擊波正壓作用時間較單點爆炸時大，峰值較單點爆炸時稍低，綜合作用的沖量(3 ms時刻)比單點爆炸時大35.8%。此后，沖擊波在艙室內開始趨于勻化，逐步形成準靜壓，兩種條件下的B2點沖擊波沖量的差距隨時間增加而逐步減小(如表5)。

該船艙艙壁結構的自振周期T為14.9 ms，T/5=3.0 ms，大于該條件下的沖擊波作用脈寬，適用沖量準則。T/5(3.0 ms)內的沖擊波沖量對艙室的毀傷有效，所以選取3.0 ms時刻的沖量進行對比。與之相對應的是，條件B的艙室變形量比條件A大57%。

表5 同等藥量不同條件下中心面B2沖量表

5 結論

通過等效縮比艙室模型的內爆炸試驗，研究了雙點裝藥同步內爆炸的爆炸效應特征，對比分析了雙裝藥同步爆炸和同質量單裝藥爆炸對艙室毀傷效果的差異。研究發現，在總裝藥質量相同時，雙點爆炸下橫隔壁處的沖量比單點爆炸時大35.8%，上板變形量比單點爆炸時大57%。相比同等裝藥質量單點爆炸，雙點裝藥爆炸時沖擊波在裝藥中心區域上相互疊加，可增大該處的沖擊波沖量，有效提高對該類縮比艙室的毀傷能力。

[ 1 ] 鄧國強, 龍汗, 周早生, 等. 鉆地彈砂土中聚集爆炸地沖擊試驗與預測[J]. 防護工程, 2001(3): 24-28.

DENG Guoqiang, LONG Han, ZHOU Zaosheng, et al. Shock test and firecast of the gathering explosion for the earth penetrator in sandy soil [J]. Protection Engineering, 2001(3): 24-28.

[ 2 ] 陳朗, 魯建英, 馮長根. 多點起爆炸藥形成平面波數值模擬分析[J]. 含能材料, 2004, 12: 493-496.

CHEN Lang, LU Jianying, FENG Changgen. Numerical simulation of multi-point initiation of explosives to form planar shock waves[J]. Energetic Materials, 2004, 12: 493-496.

[ 3 ] 張洋溢, 龍源, 紀沖, 等. 沖擊波疊加效應對組合式多爆炸成型彈丸成形的影響研究[J]. 振動與沖擊, 2012, 31(1): 56-60.

ZHANG Yangyi, LONG Yuan, JI Chong, et al. Superposition effect of shock waves on formation of a grouped multiple explosive formed projectile [J]. Journal of Vibration and Shock, 2012, 31(1): 56-60.

[ 4 ] 孫百連, 顧文彬, 蔣建平, 陽天海. 淺層水中沉底的兩個裝藥爆炸的數值模擬研究[J]. 爆炸與沖擊, 2003, 23(5): 460-465.

SUN Bailian, GU Wenbin, JIANG Jianping, et al. Numerical simulation of explosion shock wave interaction in shallow-layer water[J]. Explosion and Shock Waves, 2003, 23(5): 460-465.

[ 5 ] 陳志林. 關于多點爆炸效應的初步探討[C]. 爆炸作用及其防護學術交流會和學組會成立會. 洛陽: 總參工程兵科研三所, 1988.

[ 6 ] 林大超, 白春華, 張奇. 爆炸地震地面豎向振動的幅值特性[J]. 北京理工大學學報, 2001, 21(2): 173-176.

LIN Dachao, BAI Chunhua, ZHANG Qi. Amplitude characteristics of vertical ground surface vibration caused by explosion seism[J].Journal of Beijing Institute of Technology, 2001, 21(2): 173-176.

[ 7 ] 國勝兵, 潘越峰, 高培正, 等.爆炸地震波模擬研究[J]. 爆炸與沖擊, 2005, 25(4): 335-340.

GUO Shengbing, PAN Yuefeng, GAO Peizheng, et al. Numerical simulation of explosion seismic waves[J]. Explosion and Shock Waves, 2005, 25(4): 335-340.

[ 8 ] 顧文彬, 孫百連, 陽天海, 等. 淺層水中沉底爆炸沖擊波相互作用數值模擬[J]. 解放軍理工大學學報(自然科學版), 2003, 4(6): 64-68.

GU Wenbin, SUN Bailian, YANG Tianhai, et al. Numerical simulation of explosive shockwave interaction in shallow-layer water[J]. Journal of PLA University of Science and Technology, 2003, 4(6): 64-68.

[ 9 ] 李旭東, 劉凱欣, 張光升, 文尚剛, 譚福利, 葉琳. 沖擊波在水泥砂漿板中的聚集效應[J]. 清華大學學報(自然科學版), 2008, 48(8): 1272-1275.

LI Xudong, LIU Kaixin, ZHANG Guangsheng, et al. Focusing of shock waves in cement mortar plates[J]. Journal of Tsinghua University of Science and Technology, 2008, 48(8): 1272-1275.

[10] 張世豪,韓晶,王華,等.混凝土中多點同步爆炸能量聚集效應分析[J]. 爆破, 2014, 31(1): 19-24.

ZHANG Shihao, HAN Jing, WANG Hua, et al. Energy gathering effect of muti-point simultaneous explosion in concrete[J]. Blasting, 2014, 31(1): 19-24.

[11] 胡宏偉, 宋浦, 郭煒, 等. 地面爆炸沖擊波的相互作用[J]. 高壓物理學報, 2014, 28(3): 353-357.

HU hongwei, SONG Pu, GUO Wei, et al. Interaction of shock waves in ground burst[J]. Chinese Journal of High Pressure Physics, 2014, 28(3): 353-357.

[12] 王龍侃, 張之凡, 郎濟才, 等. 基于LS-DGF-DG方法的船體板架結構近場水下爆炸毀傷特性研究[J]. 振動與沖擊, 2016, 35(16): 64-71.

WANG Longkan, ZHANG Zhifan, LANG Jicai, et al. Damage characteristics of hull grillage subjected to near-field underwater explosion based on an LS-DGF-DG method [J]. Journal of Vibration and Shock, 2016, 35(16): 64-71.

[13] 顧平安, 衛海鷹, 肖昌炎. FAE云霧爆轟沖擊波壓力測試技術研究[J]. 爆炸與沖擊, 2001, 21(4): 311-314.

GU Pingan, WEI Haiying, XIAO Changyan. Studies of the shock-wave measuring technology in the FAE test[J]. Explosion and Shock Waves, 2001, 21(4): 311-314.