考慮行波效應的沉管隧道抗震性能：振動臺陣試驗研究

張學明， 閆維明， 陳彥江， 陳適才， 陳紅娟

(1. 北京工業大學 工程抗震與結構診治北京市重點實驗室, 北京 100124； 2. 北京工業大學 城市與工程安全減災教育部重點實驗室, 北京 100124； 3. 中國地震局地球物理研究所，北京 100081)

沉管隧道具有對地質水文條件適應能力強、可淺埋、與兩岸道路銜接容易、坡度小、防水性能好、工期短等優點，已被廣泛應用于城市建設中[1]。沉管隧道由多節位于水下的管段拼接而成，埋置位置一般較淺，且多修建于軟弱地層中，容易出現問題并可能導致整條隧道喪失使用功能的薄弱環節在于其接頭的連接處，因此對管段接頭的性能有著很高的要求[2]。地震荷載的作用將會影響沉管隧道整體的穩定性，造成接頭處拉伸破裂，一旦破壞將產生災難性的后果，且難于修復，因此，對沉管隧道及其接頭進行地震響應分析，研究隧道和接頭抗震性能十分重要[3]。

近年來，國內外很多學者對沉管隧道進行了研究，Anastasopoulos等[4]采用梁-彈簧模型對深水條件下沉管隧道的非線性抗震進行了分析；Oorsouw[5]研究了地震作用下隧道采用不同接頭形式時接頭部位的力學性能和變形特點；Lyngs[6]采用不同的方式進行建模來探討沉管隧道抗震設計中的模型精度問題，論文進行了大量的參數分析，結論表明，土參數、層理參數和震級對沉管隧道的破壞有較大影響；傅繼陽等[7]采用彈性地基梁理論計算了廣州洲頭咀沉管隧道的地震響應；劉鴻哲等[8]采用響應位移法和Winkler地基梁頻域分析方法對港珠澳大橋海底沉管隧道工程進行了縱向地震響應計算，并對兩種方法進行了討論和評價。另外，國內學者進行了一系列土與地下結構的振動臺試驗研究。季倩倩[9]通過輸入不同頻率的地震波對地鐵車站接頭結構模型進行了振動臺試驗，來觀測接頭結構-土體體系的加速度反應；Chen等[10]進行了埋地管土相互作用非一致激勵振動臺模型試驗研究，探討了非一致地震激勵下的有接頭埋地管線-土的反應規律及發展變化過程，結果表明地下長線型結構需要考慮非一致地震作用的影響。沉管隧道結構也屬于地下長線型結構，目前國內外研究者對其抗震性能進行了較多的數值分析研究，而針對沉管隧道及其接頭的振動臺試驗研究文獻較少，且沉管隧道結構型式不同于其它地下結構，其結構及接頭的受力性能也不同，鑒于管段和接頭處的動力反應復雜性，通過模型試驗對沉管隧道動力反應進行試驗研究，分析其整體結構以及接頭的動力響應規律是比較直接的方法。

本文為研究沉管隧道結構的抗震性能，以廣州洲頭咀沉管隧道為背景，利用振動臺陣對沉管隧道結構模型的地震響應進行試驗研究，并通過考慮一致和非一致地震作用來研究沉管隧道結構及其接頭的動力響應規律，從而為此類結構的抗震性能分析與設計提供參考依據。

1 工程概況

廣州洲頭咀沉管隧道以花蕾路與花地大道交點為起點，止點為T13路與寶崗路交點，全長3 253.034 m，其中珠江中340 m長為沉管段，共分四節段，每節段為85 m，管段接頭采用柔性接頭，其中接頭的GINA止水帶是沉管隧道接頭密封性的重要保障，其受力狀態是反應接頭結構壽命和止水性的關鍵。洲頭咀變截面隧道(沉管段)的巖土工程勘察報告表明，該沉管隧道底部位于不同物理力學性質的巖土層上，且場區巖性變化大，部分地段強風化帶與弱、微風化帶呈互層狀，使該沉管隧道所在位置的場地土地震響應較為復雜。

2 試驗設計

本文選取340 m長四節沉管隧道為參考模型，結合北京工業大學9子臺模擬地震振動臺陣系統，按照1/60的幾何相似比對振動臺試驗模型進行設計。臺振系統具體參數見表1。

2.1 相似比設計

沉管隧道模型以長度l、密度ρ、和彈性模量E為基本未知量，根據量綱分析理論，其它未知量可以用基本未知量來表示。采用忽略重力模型，即忽略Sg=1的相似要求，SE、Sl和Sρ可以自由獨立選取。結合振動臺陣試驗的現場條件，將沉管隧道試驗模型的尺寸相似比取為1/60，結構模型采用微粒混凝土制備，配筋采用鍍鋅鋼絲網，通過試驗制備的模型結構微粒混凝土配合比為水泥(425#)∶黃砂∶石灰∶水=1∶6.0∶0.6∶0.5，其彈性模量為7 410 N/mm2，立方體抗壓強度為5.679 N/mm2，密度與原型混凝土大致相同，故密度相似比取為1，彈性模量相似比為1/4。試驗所采用的動力相似系數見表2。

表1 九子臺陣系統技術參數

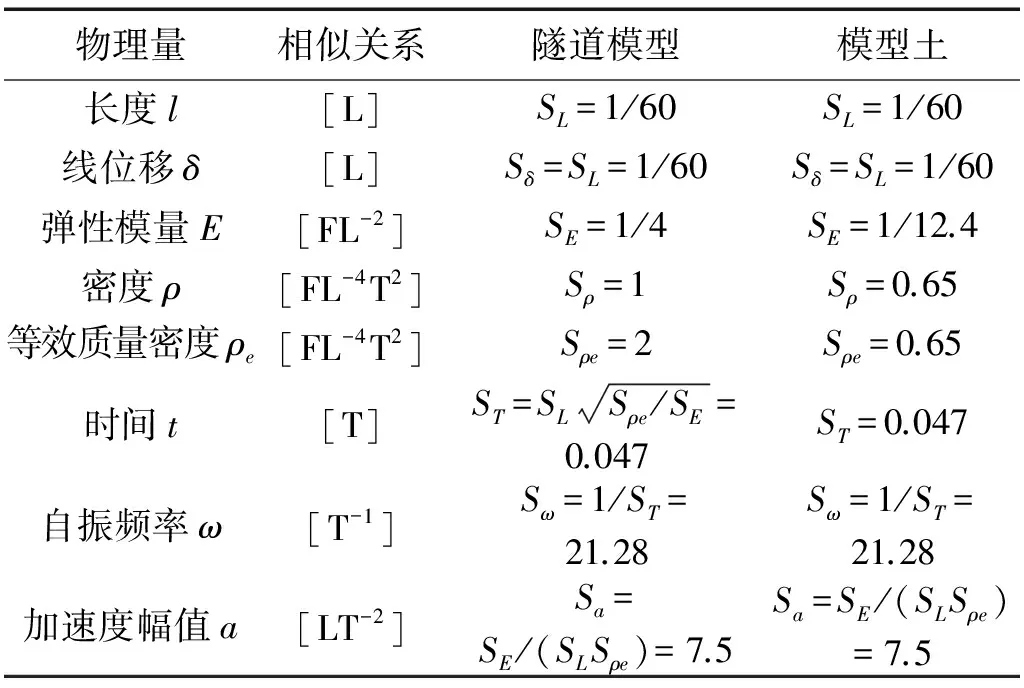
表2 模型結構及模型土的相似比

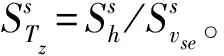
(1)

式中：m為模型；P為原型。

對于本文模型，根據相似比推導可得

(2)

根據原型隧道地質勘察報告，取場地土的等效剪切波速為300 m/s，由公式(2)可得模型土的等效剪切波速為106.1 m/s。

為得到模型土合理的等效剪切波速，本試驗采用摻和鋸末的方法，試驗所用原型土取自北京磁器口地鐵站，并加水飽和，對不同配比下的鋸末土進行試驗[11]，最終確定的配比為鋸末∶土∶水=1∶3∶2.7。模型土高取0.8 m。原型隧道上覆土厚度為2.29 m，水深6 m，水密度為1 g/cm3，土密度為2 g/cm3，將水折算成土深為3 m，根據相似比，最終確定模型隧道上覆土的厚度為14 cm。

2.2 模型的設計與制作

由于沉管隧道埋置于水下的土體之中，實驗時需要模擬的對象除了沉管隧道結構本身外，還需要模擬結構周邊的地層，這就需要在結構振動臺上另外增加一個能夠傳遞振動作用到試驗對象的裝置-模型箱[12]。在自然條件下，地基土無邊界限制，而在振動臺試驗中，由于模型箱尺寸的限制，因此，只能用有限的容積裝土來模擬無限土體。箱體邊界上的波動反射以及體系振動形態的變化將會給試驗結果帶來一定的誤差，即所謂的“模型箱效應”[13]。

本文所設計的裝配式模型箱是為實現沉管隧道在一致和非一致地震激勵下的振動臺臺陣試驗而設計，模型箱的結構和制作滿足以下要求[14]：①控制模型土箱的邊界效應，盡可能使模型土與邊界面的接觸條件能真實反應原場地的地震響應。②保證模型箱各個箱體之間的可靠連接和整體穩定性，避免在激振過程中失穩破壞。③避免模型箱與模型土因自振頻率相近而發生共振。④模型箱的尺寸、容積等參數應滿足振動臺設備臺面尺寸的承載能力的要求。⑤實現模擬單點和多點地震動輸入。

用于此次沉管隧道的模型箱為剛性連續體模型箱，考慮邊界效應問題及振動臺的承載能力，模型箱尺寸為7.3 m×2.8 m×1.2 m(縱向×橫向×高)，使用四個振動臺，每個振動臺間距為1 m，由此將模型箱分成四部分，其中，兩個邊箱的凈尺寸為1.5 m×2.8 m(縱向×橫向)，兩個中間箱的凈尺寸為2 m×2.8 m(縱向×橫向)，每個鋼箱之間的間距為0.1 m，箱框架用70 mm×70 mm×5 mm的角鋼焊接而成，如圖1。底板厚1 cm，為防止土體過重導致底板變形以及底板過薄而產生振動，鋼板下焊接工字鋼和加勁肋。鋼框架里布置15 mm厚橡膠板，橡膠板內部是200 mm泡沫板，其中，橡膠板和剛框架用小螺栓連接，橡膠板和泡沫直接用泡沫膠密封，鋼箱底板用鋼板連接。兩箱之間的外框架用螺栓將100 mm×100 mm方鋼管與角鋼連接，考慮一致地震時，將四個鋼箱連成一體，保證箱子的整體性，考慮非一致地震激勵時，將底板連接板螺栓和方鋼管卸掉，使箱體分開，但橡膠板和泡沫板不分開，保證里面土的整體性，從而滿足試驗要求[15]。

圖1 裝配式模型箱Fig.1 Fabricated Model box

沉管隧道水下共四段，其中兩端的管節為變截面管段，中間兩段為等截面管段，管段之間共有三個接頭。接頭主要由端鋼殼、GINA止水帶、Ω止水帶、剪切鍵和預拉索組成。GINA止水帶寬18 cm，長度為16.6 cm，接頭通過止水帶以及預拉索提供軸向剛度，38套預拉索總拉伸剛度約為83 406.2 kN/m，止水帶通過有限元模擬結果可知其壓縮剛度可以簡化為雙線性模型，并且，由于初始壓縮量為50 mm，所以接頭軸向壓縮剛度主要為止水帶壓縮剛度，接頭拉伸剛度主要為預拉索拉伸剛度(如圖2(c)所示)。接頭模型簡化為半剛性接頭，制作時，隧道模型采用微粒混凝土，接頭處預埋角鋼，并與端鋼殼焊接，由于原型止水帶較小，若與結構采用同樣相似比制作則過薄而無法進行試驗，而接頭止水帶的響應又是沉管隧道密封安全性的重要部分，因此本實驗止水帶采用壓縮剛度相似進行設計，從而可以增加了厚度和寬度，為了方便止水帶制作去掉尖頭，簡化預壓縮的影響。模型止水帶簡化為與隧道等截面，厚度為2 cm的橡膠圈，并與端鋼殼粘接牢固。水平及垂直剪切鍵是厚度為2 mm的矩形環，剪切鍵的一端與端鋼殼焊接牢固，另一端為自由端，使其可以自由插入一個截面較大的矩形活動鋼圈。預應力鋼拉索簡化為細螺桿，如圖3所示。在圖3(c)中，一端安裝止水帶，并采用細螺桿施加預應力，在吊裝及隧道埋置過程中，為防止隧道接頭變形過大而先用粗螺桿固定，再回填土之前將其擰松。另一端安裝拉壓力傳感器來測量隧道的軸力，每個接頭安裝四個，均分布在上下端部。

模型土拌制完成后迅速裝箱，并每10 cm進行一次夯實，裝完之后頂層覆蓋塑料薄膜來防止水分蒸發，并放配重塊進行靜壓。

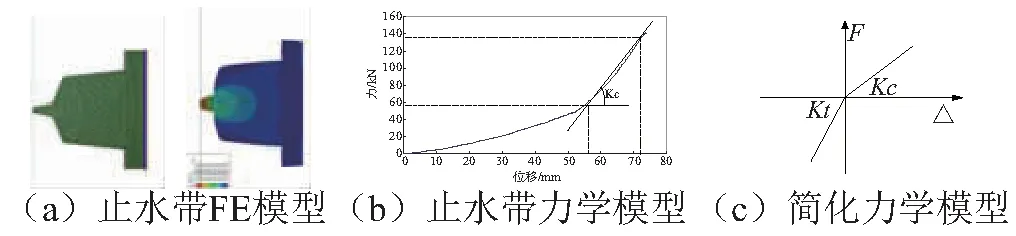
圖2 接頭簡化模型Fig.2 The simplified joint model

圖3 沉管隧道模型接頭Fig.3 The joint model of immersed tunnel

2.3 測點布置

試驗中采用加速度傳感器、拉壓力傳感器、激光位移計來進行量測。其中，各傳感器的布置如圖4，本文定義沿沉管隧道長度方向為縱向，垂直于長度方向為橫向。其中A1～A4分別測量沉管隧道縱加速度反應；A5～A7分別測量接頭處的縱向加速度反應；A8～A11測量土體縱向沿不同埋深的加速度反應。三個接頭分別安裝激光位移計來測量接頭處的相對位移，并在接頭的四角安裝拉壓力傳感器來測定接頭軸力。

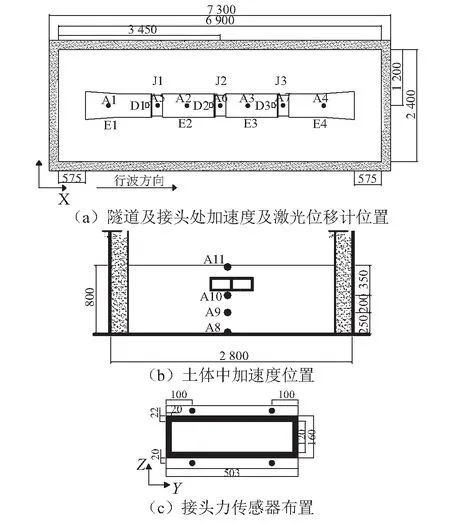
圖4 試驗測點布置圖Fig.4 Measuring points arrangement of the test

2.4 試驗工況

為了模擬行波效應對沉管隧道及其接頭處地震激勵帶來的時間遲滯，假設波沿X方向進行傳播。相鄰振動臺作動器接受指令的時間差△t=D/va，考慮到振動臺的精度和為了使時間遲滯較為明顯，取D為原場地的實際長度，va為假定的視波速，加速度時程將分別按照視波速va為100 m/s，200 m/s，300 m/s，600 m/s及無窮大(一致激勵)五種不同的形式進行X向輸入，從而說明行波效應對沉管隧道整體及其接頭處地震響應的影響。根據原型結構所在的場地特點，選用了chi-chi地震波作為地震輸入，在試驗中縱向加速度幅值從0.06 g逐漸增大至0.4 g。

3 試驗結果與分析

3.1 土與隧道加速度響應

圖5給出了土中的加速度A10在不同視波速下隨著地震激勵逐漸增大時的峰值變化情況，從圖中可以看出，除600 m/s的情況外，在輸入地震動峰值小于0.19 g時，土體在A10測點的加速度峰值響應線性關系較好，當輸入的地震動大于0.19 g時，峰值則呈現非線性。圖6是在0.12 g和0.26 g的地震動峰值輸入下土和隧道在不同視波速作用下的峰值放大系數，從圖6中可以看出，在一致激勵時，0.12 g下土與隧道的峰值放大系數分別為1.63和1.65，較為接近；而0.26 g下分別為1.42和1.56，相差較大。隨著輸入的地震波強度的增大，加速度放大系數卻明顯變小，其原因為：隨著振動強度的增加，土體非線性加強，土體傳遞振動的能力減弱。考慮行波效應后，在0.12 g時，隧道的峰值放大系數大于土體，而在0.26 g時，除了視波速為300 m/s的情況之外，隧道的加速度峰值放大系數均小于土體，其原因可能為：土體的非線性因素以及在較大地震動輸入時，考慮行波效應會使土與隧道之間出現滑移，從而導致土體傳遞到隧道上的振動能力減弱。

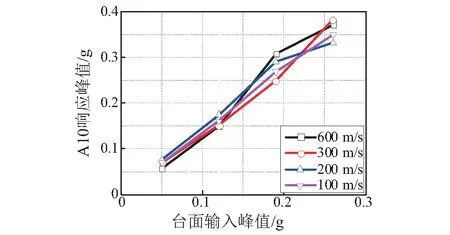
圖5 土體的加速度峰值 (A10)Fig.5 Peak value in soil (A10)

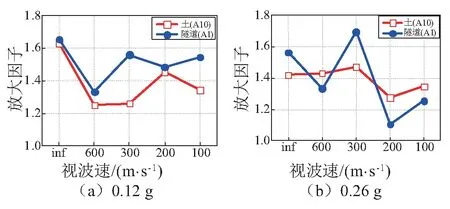
圖6 土與隧道的峰值放大系數Fig.6 Acceleration amplification factor of soil and tunnel

為研究土與隧道之間的相互作用規律，取土體在線性較好的工況下進行分析，圖7給出了臺面采集峰值為0.12 g時土體中緊鄰隧道的加速度A10和隧道頂部加速度A4在一致和考慮行波效應時不同視波速下的加速度時程及傅里葉譜圖。從圖中可以看出，一致地震激勵下，兩個測點的加速度時程曲線吻合度較好，說明隧道和土體運動較為一致。考慮行波效應后，土體較隧道的加速度曲線出現了滯后，且隧道視波速的減小，時滯效應越明顯，從頻譜圖看，一致激勵下，隧道和土體上的測點所測得頻譜曲線趨勢較好，但隧道的頻譜峰值小于土體，振動能量在從土體傳遞到隧道時會有損失，行波激勵下，傅式譜在低頻部分呈現多峰值現象，頻譜組成較一致激勵更為豐富，且最高峰值從右向左移動，說明在行波激勵下，隨著視波速的變化，模型土體的剛度也發生變化。

圖7 土與隧道結構的加速度響應Fig.7 Acceleration responses of soil and tunnel

3.2 接頭加速度響應

圖8為三個接頭在一致及行波激勵下的加速度時程及其傅式譜圖，一致激勵下，三個接頭的加速度峰值分別為0.235 g、0.202 g和0.221 g，均大于A10點的峰值，說明接頭處的振動較周圍土體振動相比更為強烈；頻譜圖則與土體中A10測點的傅式譜圖相似，頻譜范圍在30 Hz以內，且集中于10 Hz左右；視波速為600 m/s時，三個接頭的加速度峰值變小，各接頭的縮小的倍數分別為0.847、0.777和0.647，從其頻譜圖可以看出，與一致激勵相比，考慮行波效應后，頻譜幅值稍小，并呈現多峰現象，頻帶分布更為寬泛，頻譜組成更加豐富；在視波速為300 m/s時，接頭1的尖峰較多且很明顯，分布頻帶較廣，接頭3的峰值較弱。

3.3 接頭軸力

因接頭鋼拉索的初始預拉力在實測過程中誤差較大，因此本文將初始量測時的力作為力平衡位置，將其值調整在零刻度線附近。圖9為接頭受到一致和行波激勵下軸力時程圖。一致激勵下，在2 s附近接頭1以壓力為主，接頭3以拉力為主，且4 s之后接頭1和3處于受拉狀態，接頭2處于受壓狀態。從峰值來看，接頭2所受的軸力變化范圍最小，三個接頭的最大拉力和壓力均小于120 N，說明一致激勵下隧道和周圍土體保持了同步的運動，隧道運動的整體性較好，從而使其各管節之間的內力較小。在視波速600 m/s的情況下，接頭時程圖發生較大變化，兩個方向的軸力放大倍數接近十倍，接頭1在初始振動時受到較大的拉力，隨后在零刻度線上下往復變化；接頭2在初始振動時受拉，而后以受壓為主；接頭3則以受拉為主，但其最值出現在受壓時刻。視波速為300 m/s時的時程圖與600 m/s的工況較為接近，不同之處在于300 m/s時軸力變化范圍稍小。不同激勵下三接頭均有殘余軸力，其中接頭1和接頭3為殘余拉力，接頭2為壓力。各工況下接頭軸力的拉力和壓力峰值如圖10，一致激勵下接頭3的拉力最大，接頭1的壓力最大，接頭2的拉力和壓力最小；行波激勵下的最大拉力和最大壓力分別出現在接頭1和接頭3，接頭2的拉壓力均是最小值，其中，最大拉力出現在100 m/s時，達到1 436 N，與一致激勵相比放大27.6倍，最大壓力出現在200 m/s，其值為1 594 N，較一致激勵放大19.4倍。說明行波激勵下，由于輸入的地震動具有時滯，導致隧道的運動變得不一致，從而增加了管節之間的相互作用，使管節的內力顯著增加。另外，根據相似關系換算原型隧道接頭最大軸力為20 822 kN，預拉索的平均拉應力為20.9 MPa，考慮原型接頭預拉索初始預拉應力2 MPa，因此預拉索處于彈性范圍內。

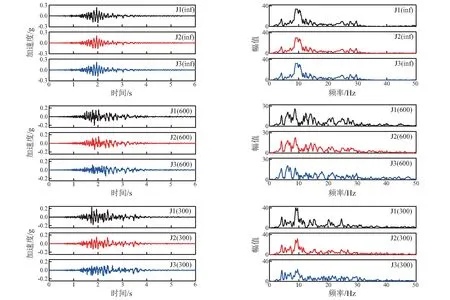
圖8 接頭測點的加速度時程及其傅式譜圖 (inf表示一致激勵；600表示視波速600 m/s，下同)Fig.8 Acceleration and corresponding spectrum of joints

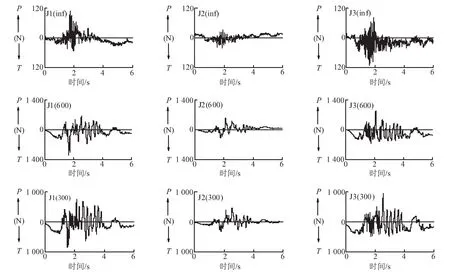
圖9 接頭軸力圖 (圖中P為受壓、T為受拉，下同)Fig.9 Axially force of joints

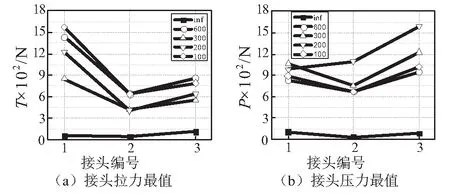
圖10 接頭軸力最值Fig.10 Maximum axial force of joints

3.4 接頭彎矩

圖11為三個接頭沿Z軸和Y軸的彎矩圖，從圖11(a)中可以看出，在一致激勵下，接頭沿Z軸方向的彎矩較小，且接頭1和接頭3的彎矩以正值為主，說明兩個接頭的彎曲方向相同，行波激勵下，接頭1的彎矩以負向為主，在300 m/s時最值達到-75 N·m，說明考慮行波效應后接頭1的軸力分布發生較大變化；對比同工況下的三個接頭可以發現，彎矩沿行波輸入方向依次減小。從沿Y軸的彎矩來看，接頭1和接頭3在行波激勵下彎矩增長較大，表現為兩個接頭的彎曲方向相反，且視波速的變化對兩個接頭的最值和時程圖變化影響不大，相比之下，接頭2的變化較小，這是由于接頭2處于中間位置，受兩端隧道約束，不容易發生彎曲。比較兩方向的彎矩可知，Y方向(水平)彎矩大于Z方向(豎直)彎矩，這是由于隧道側邊所受土壓力較均衡，很好地約束了隧道的水平搖擺變形，而實驗模型上覆土厚度僅為14 cm，在地震作用下，不能完全約束隧道的上下方向運動。

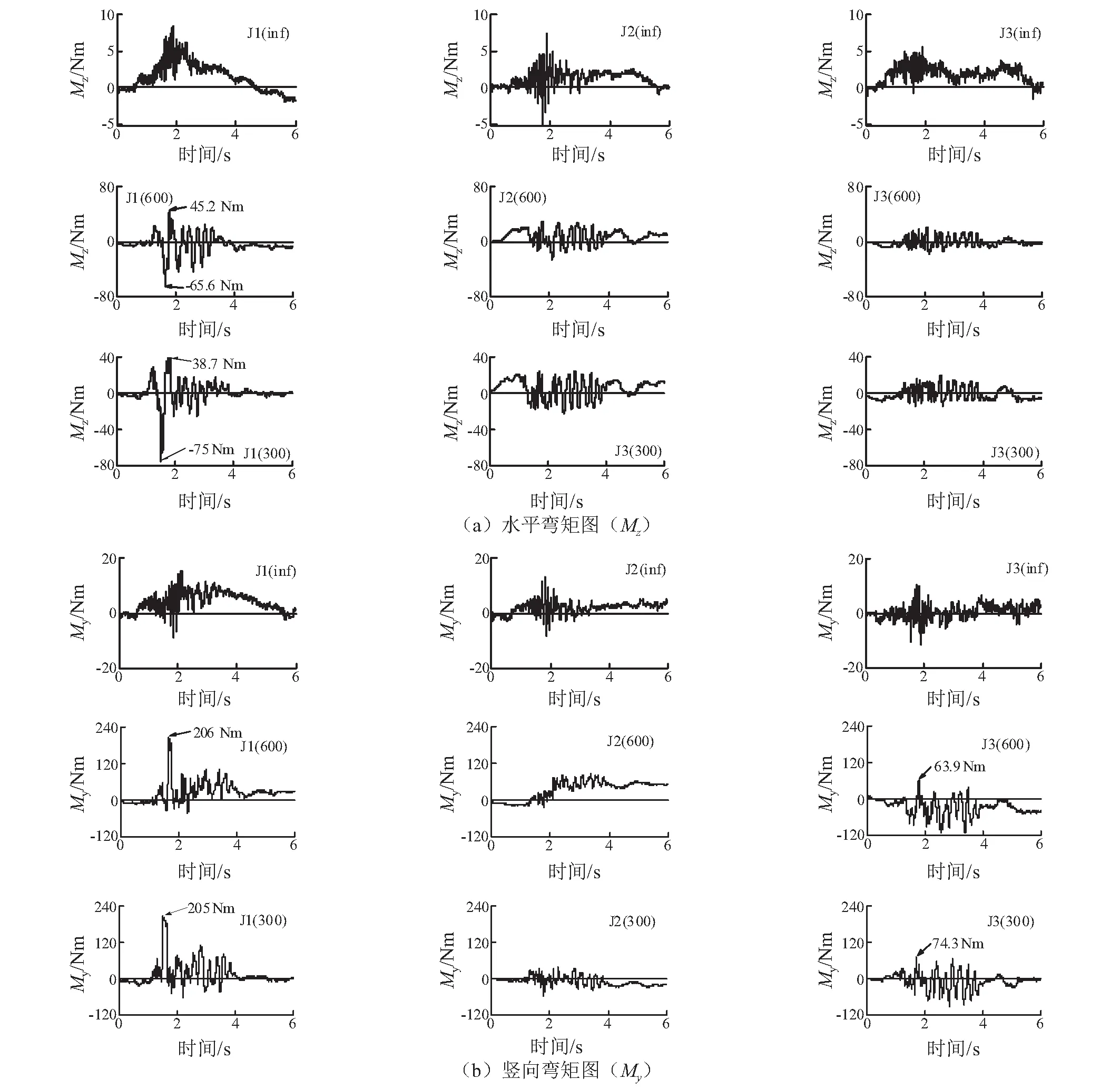
圖11 接頭彎矩圖Fig.11 Bending moment of joints

3.5 接頭變形

實際中的沉管隧道，止水帶在水壓力作用下被預壓縮，地震作用會引起止水帶出現連續的解壓和重壓縮過程，通過初始壓縮量和變形量的對比來判定隧道接頭是否失效，在模型試驗中，接頭止水帶模型比較小，又無法提供實際隧道那樣的水壓環境，因此采用拉索施加預拉力，因預壓縮量無法量測，因此本文將初始量測位置定為零點位置。圖12給出一致和行波激勵下接頭1和接頭2變形圖，從圖中可以看出，一致激勵時接頭變形非常微小，說明隧道在一致激勵下保持很好的整體運動，考慮行波效應后，接頭變形顯著增大，且同一工況下兩接頭的變形曲線趨勢較一致，但接頭1的變形要先于接頭2，且拉伸變形大于壓縮變形，此外，行波激勵下各接頭會存在比較微小的永久變形。圖13為不同視波速下接頭的拉伸和壓縮最值圖，由壓縮峰值圖可得，接頭2的壓縮量大于接頭1，且在視波速為600 m/s是壓縮量差值最大，達到0.73 mm；在拉伸峰值圖中，除600 m/s情況外，接頭2的拉伸最值均大于接頭1，且在200 m/s時得到最大拉伸量0.47 mm，根據相似關系換算原型隧道接頭最大拉伸位移為28.2 mm，小于預壓縮50 mm，因此接頭止水帶處于安全范圍。

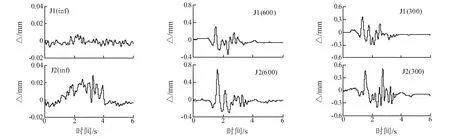
圖12 接頭變形圖Fig.12 Deformation diagram of joints

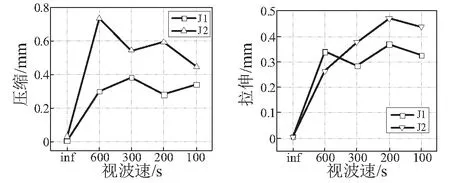
圖13 接頭變形最值 (mm)Fig.13 Maximum deformation of joints (mm)

4 結 論

本文通過設計并制作了1∶60的沉管隧道模型，并在考慮行波效應對沉管隧道的基礎上進行多子臺振動臺陣試驗，得出以下結論：

(1)一致地震激勵下，土與隧道的運動情況較為一致；通過觀測加速度變化可以看出土與隧道在行波激勵下出現滑移現象。

(2)考慮行波效應后，接頭的軸力、彎矩和位移變化較為顯著，三個接頭的軸力表現出兩端大，中間小的規律；接頭1的軸力較一致地震激勵相比放大27.6倍。

(3)雖然行波效應對隧道及其接頭的影響較為顯著，但是通過與原型隧道的換算可知，原型隧道在行波激勵下的預拉索平均應力增加很小，拉伸位移小于允許值50 mm，均在安全范圍之內。

[ 1 ] 傅繼陽, 徐安. 某沉管隧道場地土地震響應研究[J]. 廣州大學學報(自然科學版), 2009, 8(5): 64-67.

FU Jiyang, XU An. Seismic response of site soil in an immersed tunnel[J]. Journal of Guangzhou University (Natural Science Edition), 2009, 8(5): 64-67.

[ 2 ] 劉鵬, 丁文其, 金躍朗, 等. 沉管隧道接頭三維非線性剛度力學模型[J]. 同濟大學學報(自然科學版), 2014, 42(2): 232-237.

LIU Peng, DING Wenqi, JIN Yuelang, et al. Three-dimension nonlinear stiffness mechanical model of immersed tunnel joints[J]. Journal of Tongji University. 2014, 42(2): 232-237.

[ 3 ] 張如林, 樓夢麟, 袁勇. 土-海底沉管隧道體系三維地震響應分析[J]. 湖南大學學報 (自然科學版), 2014, 41 (4): 25-32.

ZHANG Rulin, LOU Menglin, YUAN Yong. Three-dimensional seismic respone analysis of soil-undersea immersed tunnel system[J]. Journal of Hunan University(Natural Sciences), 2014,41(4): 25-32.

[ 4 ] ANASTASOPOULOS I, GEROLYMOS N, DROSOS V, et al. Nonlinear response of deep immersed tunnel to strong seismic shaking[J]. Geotech Geoenviron Eng., 2007, 133: 1067-1090.

[ 5 ] VAN OORSOUW R S. Behaviour of segment joints in immersed tunnels under seismic loading[D]. Delft: Delft University of Technology, 2010.

[ 6 ] LYNGS J H. Model accuracy in aseismic design of immersed tunnel[D]. Greece: Aalborg University, 2008.

[ 7 ] 傅繼陽, 吳玖榮, 徐安. 廣州洲頭咀沉管隧道地震響應研究[J]. 湖南大學學報 (自然科學版), 2008, 35(9): 23-27.

FU Jiyang, WU Jiurong, XU An. Seismic response of Zhoutouzui immersed tunnel in Guangzhou[J]. Journal of Hunan University (Natural Sciences), 2008, 35(9): 23-27.

[ 8 ] 劉鴻哲, 黃茂松. 超長沉管隧道縱向地震響應頻域分析方法[J]. 巖土工程學報, 2015, 37(11): 1971-1978.

LIU Hongzhe, HUANG Maosong. Frequency-domain analysis method for longitudinal seismic response of super-long immersed tunnels[J]. Journal of Geotechnical Engineering, 2015, 37(11): 1971-1978.

[ 9 ] 季倩倩. 地鐵車站結構振動臺模型試驗研究[D]. 上海：同濟大學，2002.

[10] CHEN Jun, SHI Xiaojun, LI Jie. Shaking table test of utility tunnel under non-uniform earthquake wave excitation[J]. Soil Dynamics and Earthquake Engineering, 2010, 30: 1400-1416.

[11] 陳紅娟, 閆維明, 陳適才, 等. 小比例尺地下結構振動臺試驗模型土的設計與試驗研究[J]. 地震工程與工程振動, 2015, 23(3): 59-66.

CHEN Hongjuan, YAN Weiming, CHEN Shicai et al. Design and experimental research on model soil used for shaking table test of a small scale underground structure [J]. Earthquake Engineering and Engineering Dynamics, 2015, 23(3): 59-66.

[12] 袁勇, 黃偉東, 禹海濤. 地下結構振動臺試驗模型箱應用現狀[J]. 結構工程師, 2014, 30(1): 38-45.

YUAN Yong, HUANG Weidong, YU Haitao. Status of model container applications in shaking table test for underground structures[J]. Structural Engineers, 2014, 30(1): 38-45.

[13] 錢德玲, 夏京, 盧文勝, 等. 支盤樁-土-高層建筑結構振動臺試驗的研究 [J]. 巖石力學與工程學報, 2009, 28(10): 2024-2030.

QIAN Deling, XIA Jing, LU Wensheng, et al. Study of Shaking table test of squeezed branch pile-soil-high-rise structure interaction system [J]. Journal of Rock Mechanics and Engineering, 2009, 28(10): 2024-2030.

[14] 陳國興, 王志華, 左熹, 等 . 振動臺試驗疊層剪切型土箱的研制[J]. 巖土工程學報, 2010, 32 (1): 89-97.

CHEN Guoxing, WANG Zhihua, ZUO Xi, et al. Development of laminar shear soil container for shaking table tests [J]. Journal of Geotechnical Engineering, 2010, 32(1): 89-97.

[15] 張學明, 陳彥江, 閆維明, 等. 沉管隧道振動臺臺陣試驗模型土箱及適用性分析. 第二十三屆全國結構工程學術會議論文集第Ⅱ冊[C]. 北京：《工程力學》雜志社, 2014: Ⅱ-405-Ⅱ410.