基于數據融合和LMD的廠房結構動參數識別研究

王海軍， 李 康， 練繼建

(1.天津大學 水利工程仿真與安全國家重點實驗室，天津 300354；2.天津大學 建筑工程學院，天津 300354 )

隨著水輪發電機組容量和水頭的不斷提高，機組振動穩定性問題的研究日益受到重視。水電站機組運行時，廠房結構受到來自水流、機械、電磁等方面的動荷載綜合作用，因此在廠房結構的安全運行監測和動力學設計時必須重視其動力學特性[1]。水電站廠房現場振動測試是一種有效獲取廠房結構動力特性的手段。水工結構在進行振動現場測試時，由于受到各種振源的干擾，所得到的試驗數據信噪比低，一般都要對信號進行“去噪”[2]。由于水電站廠房振動測試中采用分布式測點布置，單一測點的振動信號包含結構整體信息相對有限，如何將多測點振動信號進行融合獲取廠房完整的結構動態信息具有重要意義[3]。數據融合相對于信息表征的層次可分為數據級融合、特征級融合和決策級融合。其中，數據級融合能保持盡可能多的原始數據，具有最高精度。數據級融合是直接在采集到的原始數據層上進行融合，從融合的數據中提取特征向量，獲取更準確、可靠的數據信息。對于廠房結構中相似結構或部位，振動信號中所包含結構整體動力特征相似。一致性數據融合方法能夠保留盡可能多的真實信息，對于廠房振動信號分析比較適用。傳統的水工結構振動響應濾波降噪是基于傅里葉變換的方法，根據信號的頻率分布，采用一定結構和帶寬的濾波器進行濾波。數字濾波的時域方法通過對信號離散數據進行差分方程數學運算達到濾波目的。小波閾值降噪利用變換閾值對含噪信號進行處理，然后對處理后系數進行小波重構獲得信號的有效信息，減小噪聲的影響[4]。集合經驗模式分解(EEMD)，可以有效抑制常規經驗模式分解算法處理非平穩振動信號時產生的模式混疊現象，也可以彌補小波降噪方法對調頻調幅信號處理過程中存在的特征波匹配缺陷[5]。Smith[6]提出一種新的信號分解方法——局部均值分解(Local Mean Decomposition，LMD)，LMD自適應地將信號分解為若干個乘積函數(Product Function，PF)之和，其中每一個PF可看作由一個包絡信號與一個純調頻信號的乘積得到。LMD是一種自適應時頻分析方法，可有效地緩解端點效應和減少迭代次數[7]。

本文基于一致性數據融合算法和LMD提出一種組合振動信號動態參數識別方法。首先將多測點振動信息進行數據融合，驗證融合信號所含結構整體振動信息更為全面，信噪比提高；將融合信號用LMD方法濾波降噪，可進一步分離環境噪聲；最后提取結構的真實振動信息。將其用于水電站廠房振動特性分析中，可有效地獲取結構整體動力特性，為水電站廠房動態分析提供支持。

1 數據融合及LMD方法

1.1 一致性數據融合算法

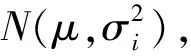
(1)

采用dij和dji作為傳感器i和傳感器j之間數據的置信距離，dij越小表示兩個傳感器的觀測值越接近，反之則表示兩個傳感器的觀測值偏差越大，其表達式為：

(2)

(3)

式中：Pi(x|xi)是條件概率；Z為服從標準正態分布N(0,1)的隨機變量，從而可得置信距離矩陣分布：

(4)

根據經驗或多次測試結果，給定一個閾值εij，令

(5)

則由傳感器之間的置信距離矩陣D可以得到傳感器之間的支持矩R為：

(6)

由支持矩陣R可以得到各個傳感器測量數據被其他傳感器測量數據的支持程度[8]。

認為一個傳感器測量數據xi被其他多數傳感器支持時，其測量數據xi為有效數據。有效數據的集合稱為融合集，融合集中數據的個數為最佳融合數l，融合集為{x1,x2,x3,…xl}，得到的最優融合數據為θ。

(7)

(8)

式中：L2(x1,x2,…,xl)為極大似然函數。

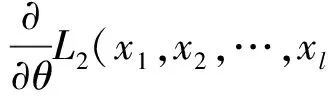
(9)

得最優融合數據：

(10)

1.2 局部均值分解

LMD方法本質上是從原始信號中分離出純調頻信號和純調幅信號，每一個PF分量由兩者相乘得到。對于任意信號x(t),其LMD的基本分解過程如下：

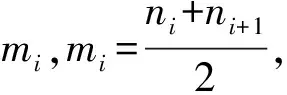
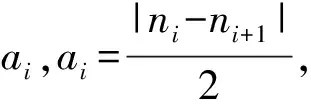
(3)將局部均值函數m11(t)從原信號x(t)中分離出來，得到：

h11(t)=x(t)-m11(t)

(11)

(4)用h11(t)除以包絡估計函數a11(t)對h11(t)進行調解，得到：

s11(t)=h11(t)/a11(t)

(12)

計算s11(t)的包絡估計函數a12(t)，假如a12(t)不等于1，說明s11(t)不是純調頻信號，需要對s11(t)重復以上迭代過程，直至-1?s1n(t)?1并且其包絡估計函數滿足a1(n+1)(t)=1

(13)

式中：s1n(t)=h1n(t)/a1n(t)

在實際運用中為減少迭代次數，提高計算速度，設置誤差ε≥0，使得1-ε≤a1n(t)≤1+ε成為迭代終止條件。

(5)將迭代過程中產生的所有包絡估計函數相乘得到包絡信號a1(t)

(14)

(6)原始信號的第一個PF分量：

PF1(t)=a1(t)s1n(t)

(15)

(7)將PF1(t)從原始信號x(t)分離出來，得到u1(t)，將u1(t)作為原始數據重復以上步驟，循環k次，直至u1(t)成為一個單調函數為止。

原始信號x(t)分解為k個PF分量和一個余量uk(t)之和，即：

(16)

2 一致性數據融合和LMD組合動參數識別

水電站廠房振動測試往往受到環境噪聲影響，混有白噪聲、水力和電磁的干擾。采用一致性數據融合算法對n個測點信號數據進行融合處理，整合與挖掘信號中整體結構動力信息，減小噪聲影響。引入去噪評價指標信噪比(SNR)衡量信息融合的效果[9]，表達為

(17)

式中：sk為原始信號；gk為調整后信號。

確定融合效果最優的閾值εij，得到融合信號y(t)；信號y(t)包含較全面的整體振動信息，但振動響應多為低信噪比信號，真實信號常淹沒于噪聲中；利用LMD將y(t)自適應分解成較高時間和頻率分辨率的PF分量，其間采用波形延拓方法對y(t)進行延拓，以抑制端點效應；然后依據各PF分量的頻譜圖，并進行各分量與融合信號的相關性分析，確定含有真實信號成分的PF分量，濾波重構信號[10]；最后對重構信號進行動參數識別。

因此這種組合方法不僅能最大程度地保留有用信號成分，而且自適應地分解噪聲信號，減小或除去噪聲成分，從而提高了獲取完整動參數的準確性。

一致性數據融合算法中閾值εij的選取直接影響融合信號的好壞，閾值實質是介于0和1之間的條件概率值。采用多次試算與融合效果判定相結合的方法確定閾值。具體步驟如下：

1)設定閾值的取值范圍[0.5 ,1]，閾值變化的步長為λ，取初始閾值為0.5。

2)按照設置的閾值對各原始信號進行數據融合，計算各原始信號在融合信號中信噪比之和(SNRsum)。

(18)

式中：Sik為第i條原始信號；gk為融合后信號；n表示原始信號個數；N表示原始信號中數據點數。

3)重新設定閾值，閾值取為上一個閾值和步長λ之和。重復步驟2)，直至閾值取為1時，停止計算。

4)選取SNRsum最大時的閾值作為融合效果最優的閾值。

其中閾值步長λ根據融合效果要求和計算效率兩方面綜合決定。上述確定閾值εij過程中SNRsum最大時，融合信號既最大程度地整合保留了各條原始信號的信息，又同時較大程度上濾除了噪聲比例較大的數據點。

為直觀了解信號降噪和動參數識別過程，建立流程如圖1。其中關鍵的步驟為：

1)計算置信距離矩陣，確定閾值，構建支持矩陣；

2)確定最佳融合參數，融合信號數據，計算各原始信號在融合信號中信噪比之和，判斷融合效果是否最優，若否，重新設定閾值，重復1)～2)步驟，直至融合效果最優。

3)融合信號波形延拓，經LMD分解出若干個PF分量，觀察并提取相應的瞬時頻率。

4)對PF分量進行頻譜分析，并利用互相關法則，提取與融合信號相關程度高的PF分量，去除噪聲分量，重構輸出信號z(t)。

5)評定降噪效果，計算信噪比SNR和均方根誤差RMSE，得到降噪后的振動信號。

6)采用常規的參數識別方法識別動參數。

3 仿真分析

為驗證本文組合降噪方法的可信性，構造3條加噪信號，其純凈信號均為：

f(t)=Ae-tπ/2sin(15t)+Be-t/3sin(20)t

(19)

式中:A和B為自由非負變量，純凈信號頻率成分不變；第一條加噪信號為f1(t)=x(t)+x1(t)+x2(t)，如下：

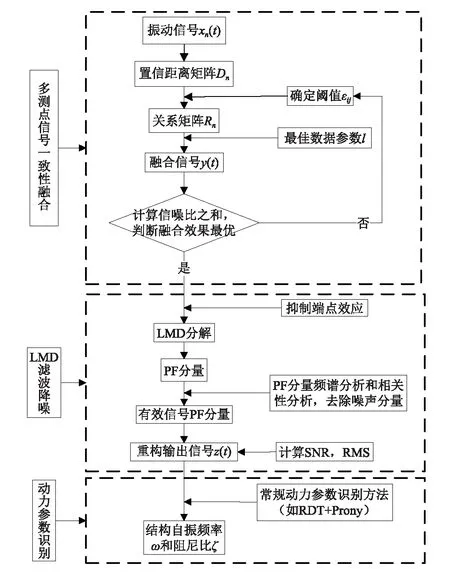
圖1 一致性數據融合與LMD組合動參數識別流程Fig.1 The flowchart of dynamic parameters identification based on consensus data fusion and LMD

(20)

(21)

白噪聲：

x2(t)=5randn(1,nn)

(22)

第二條加噪信號為f2(t)=y(t)+y1(t)+y2(t)，如下：

y(t)=15e-tπ/2sin(15t)+11e-t/3sin(20t)

(23)

(24)

白噪聲

y2(t)=8randn(1,nn)

(25)

第三條加噪信號為f3(t)=z(t)+z1(t)+z2(t)，如下：

z(t)=18e-tπ/2sin(15t)+20e-t/3sin(20t)

(26)

(27)

白噪聲：

z2(t)=10randn(1,nn)

(28)

式中：T1=0.01+0.1n, 0.02+0.1n, 0.03+0.1n，n=1,2,…,99；t為時間；采樣頻率為100 Hz，采樣時長為10 s；randn(1,nn)為均值為零、標準差為1的標準正態分布白噪聲，nn為樣本個數；x1(t)、y1(t)和z1(t)均為高頻間歇信號。設振動幅值單位為微米(μm)，純凈信號x(t)和加噪信號f1(t)的時程曲線對比見圖2，加噪信號f1(t)降噪前后的功率譜密度曲線對比見圖3。

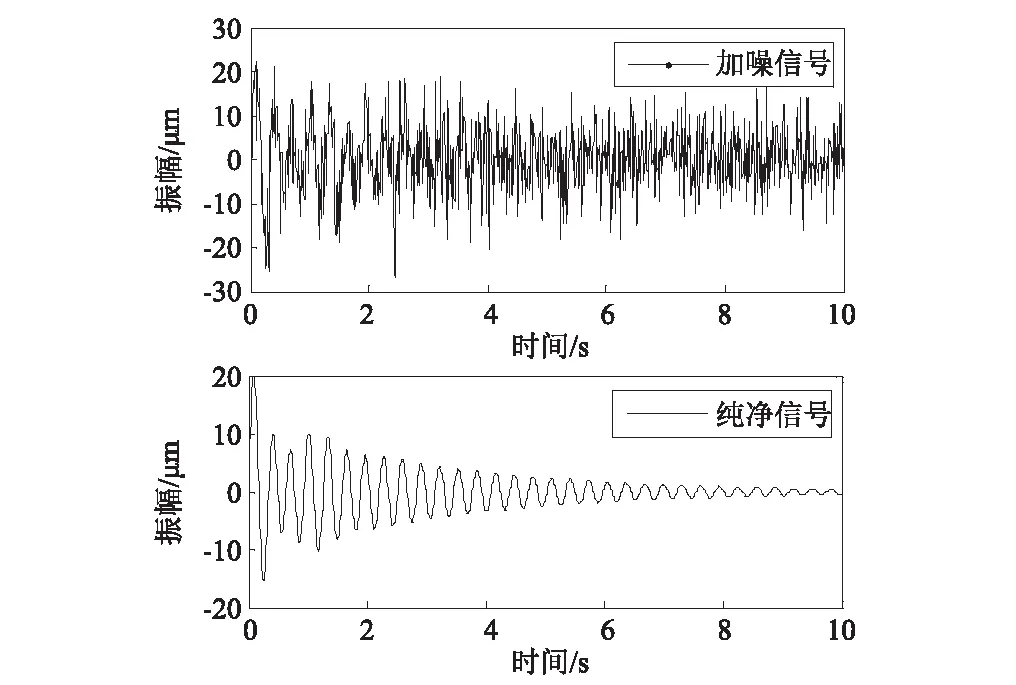
圖2 純凈信號x(t)和加噪信號f1(t)的時程曲線 Fig.2 Time history curves of pure signal x(t) and noisy signal f1(t)

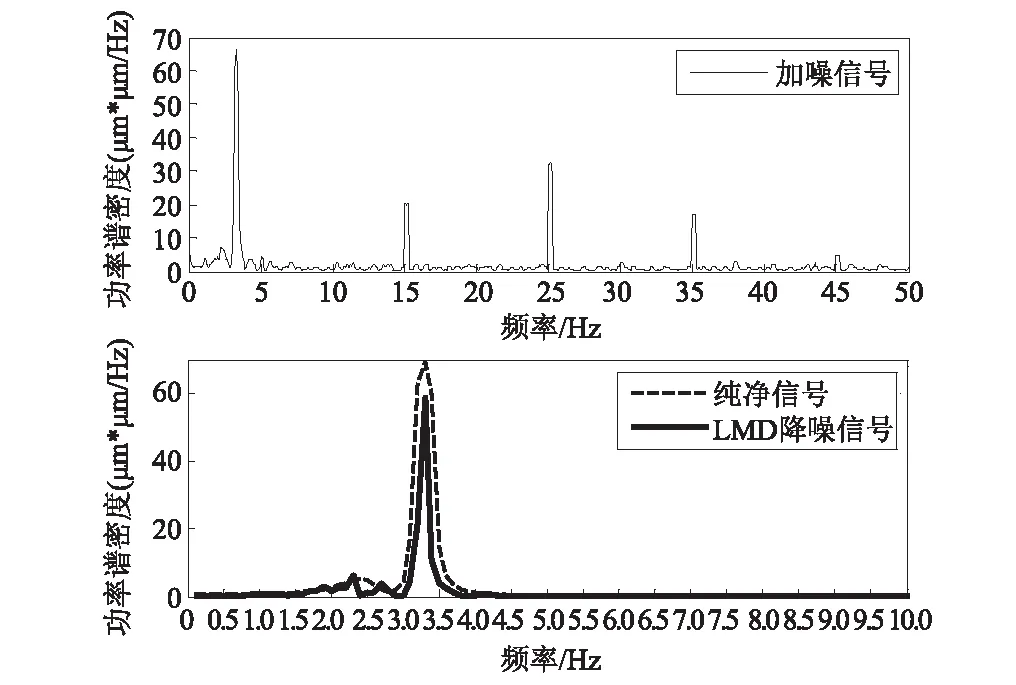
圖3 加噪信號f1(t)降噪前后的功率譜密度曲線Fig.3 The curves of power spectral density between noisy and de-noised signal f1(t)

由圖3可知，以15 Hz、25 Hz、35 Hz和45 Hz為優勢頻率的高頻噪聲和白噪聲淹沒了真實信號的部分優勢頻率，造成信號嚴重失真。分別用數字濾波、小波閾值降噪、EEMD和LMD方法對信號進行降噪處理，計算各降噪信號的信噪比SNR見表1。

表1 四種方法降噪效果指標對比

四種降噪方法中LMD降噪信號的信噪比最大，并且經過LMD降噪后，噪聲頻率被剔除，信號真實的優勢頻率得以保留。局部均值分解法(LMD)相較于其余三種降噪方法在處理類似含有“高頻噪聲和白噪聲”的信號上，具有一定的優勢和可行性。

在單一信號的降噪功率譜密度圖中，噪聲往往淹沒部分真實信號頻率或者致使信號發生混頻現象，并且由于噪聲的污染程度不相同，濾波降噪后信號的信噪比和頻率識別效果差異較大；因此采用一致性融合算法融合信號，可以最大程度上保留各信號中共有的真實信息。

信號f1(t)，f2(t)和f3(t)均為調幅信號，噪聲污染程度各不相同，其中f2(t)的噪聲部分是以5 Hz、15 Hz與25 Hz為優勢頻率的高頻噪聲和白噪聲，f3(t)的噪聲部分是以10 Hz、20 Hz與30 Hz為優勢頻率的高頻噪聲和白噪聲。但其純凈信號的優勢頻率相同和振動形式相似，可描述為不同精度的傳感器獲取的結構振動數據，或者為結構相似部位的振動數據。對信號進行融合處理有利于獲取結構振動的全面信息，減小噪聲的污染程度；采用一致性數據融合方法對f1(t)，f2(t)和f3(t)進行融合中，經試算選取閾值為0.98，形成關系矩陣，最佳融合參數l為2，各純凈信號在融合降噪信號中信噪比最大為17.72；融合信號經LMD分解為4個PF分量和1個余量u，觀察各PF分量的頻譜圖，可知PF1分量為干擾信號和白噪聲信號，然后分析各分量與融合信號的互相關性，可知PF3～PF4分量為受白噪聲污染的信號，提取PF2作為有效信號，形成輸出信號z(t)。PF1分量的功率譜密度曲線見圖4，融合信號和其降噪后信號的時程曲線見圖5，功率譜密度曲線見圖6。由圖6可知融合信號中純凈信號能量提高，噪聲能量降低，且融合降噪后信號的優勢頻率明顯，信號去噪效果較好。信號融合前后降噪效果見表2。

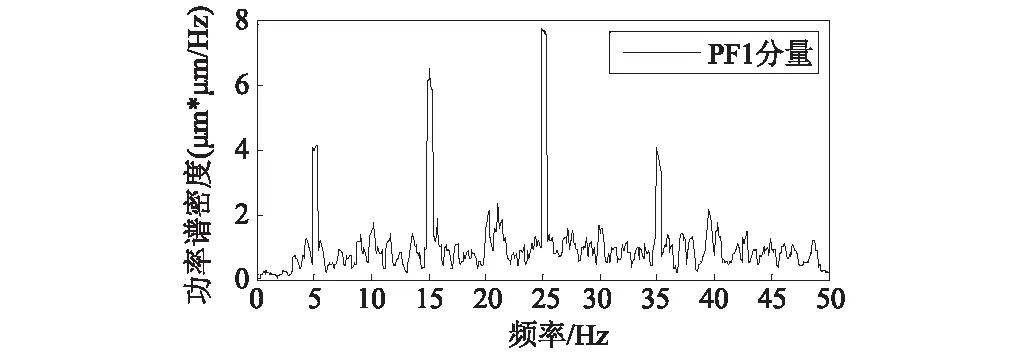
圖4 PF1分量的功率譜密度曲線Fig.4 Power spectral density curves of PF1 component

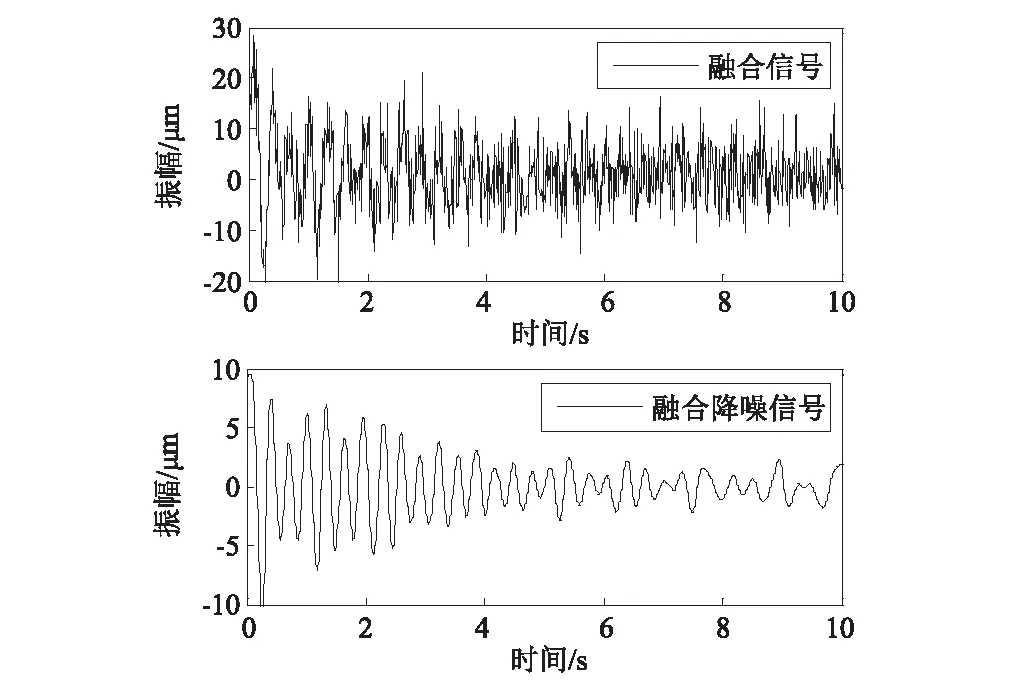
圖5 融合信號和融合降噪信號的時程曲線Fig.5 Time history curves of fused signal and de-noised signal

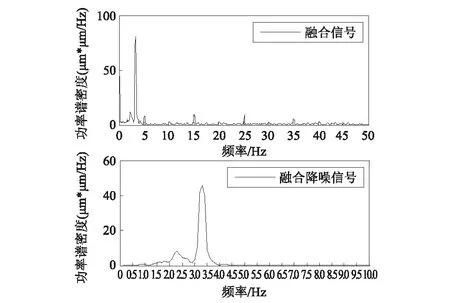
圖6 融合信號降噪前后的功率譜密度曲線Fig.6 The curves of power spectral density between fused signal and de-noised signal

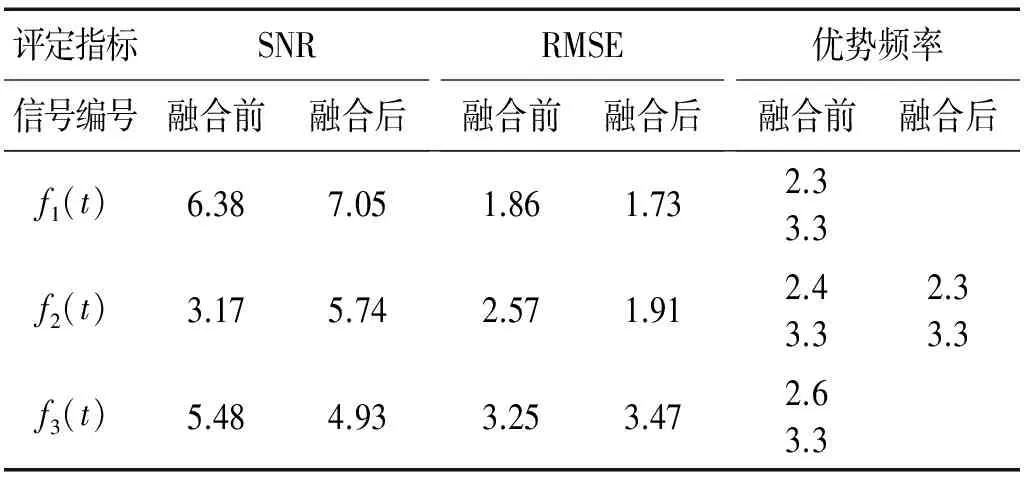
表2 信號融合前后降噪效果對比

融合前的評定指標是各單一加噪信號f1(t)、f2(t)和f3(t)去噪效果；融合后的評定指標是融合信號的去噪效果， 其中SNR和RMSE是分別以純凈信號x(t)、y(t)和z(t)為原始信號sk，融合后的降噪信號為調整后信號gk計算得出。

從表2中可知：信號融合前后其降噪效果明顯增強，純凈信號x(t)和y(t)在融合后的降噪信號中信噪比顯著提高，雖然信號z(t)在融合后的降噪信號中信噪比小幅減小，但融合降噪信號的優勢頻率更接近z(t)的真實頻率；采用一致性數據融合方法對數據進行融合，融合信號能更真實地反映信號中特征信息，減小噪聲對信息的污染程度。故一致性數據融合和LMD組合方法在處理含有較高頻率的干擾噪聲和白噪聲的低信噪比信號方面具有有效性。

4 工程實例

以一大型水電站地下式廠房振動原型觀測試驗為依托，分別在廠房結構的發電機層和電氣夾層吊物孔、樓梯口處，電氣夾層牛腿處分別設置測點，選取機組停機過程中廠房結構振動觀測數據，采用本文方法對5個測點的數據進行數據融合和LMD處理，然后運用隨機減量法(RDT)和復指數法(Prony)進行廠房結構模態參數識別；測點具體位置見圖7。截取停機過程振動信號中反映廠房自由衰減振動的信號作為分析數據，截取實測信號時長為10 s，采樣頻率為400 Hz，其中在測點1～4處提取樓板垂向振動數據，測點5處提取牛腿橫河向振動數據，各測點振動時程曲線見圖8。

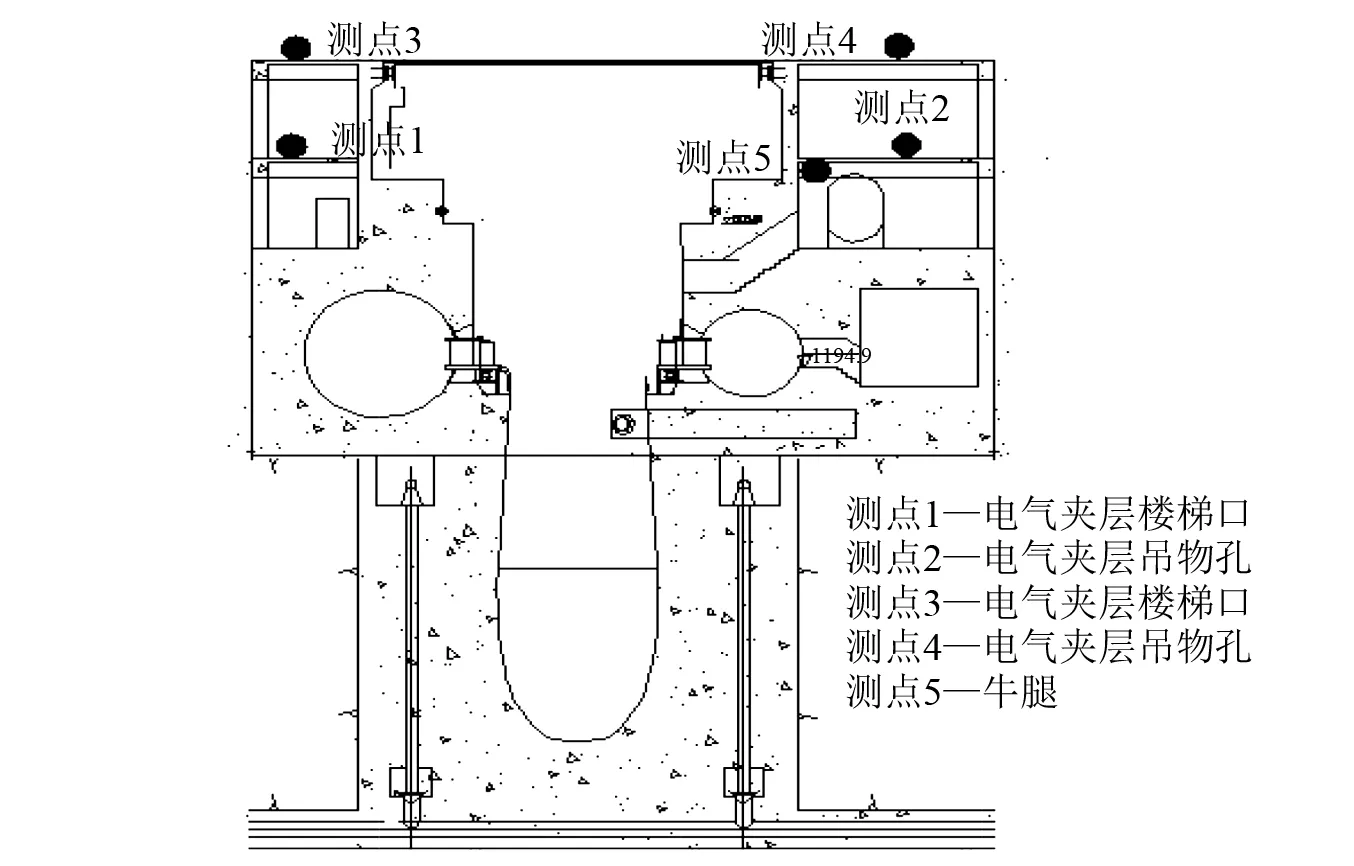
圖7 水電站廠房結構測點布置圖Fig.7 The measuring point chart of hydro-powerhouse structures

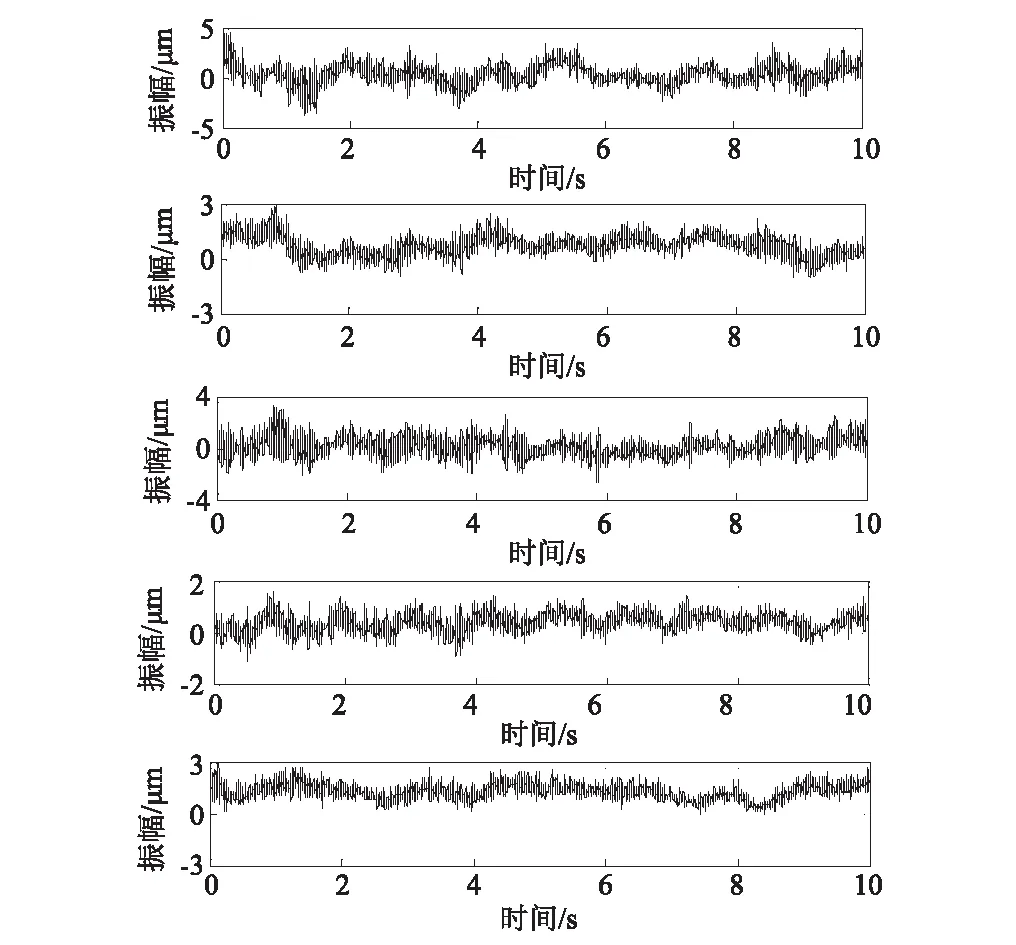
圖8 停機過程中測點1～5處的振動時程曲線Fig.8 Time history curves of points 1～5 in the outage process

根據圖1中算法流程，利用本文方法對廠房結構動力參數進行識別，由于5個測點數據是結構不同方位的振動數據，首先對數據進行振幅歸一化處理，經試算，融合處理中確定閾值為1，最佳融合參數l為4，各測點信號在融合信號y(t)中的信噪比之和為3.78，最大程度地保留了結構整體振動的信息。然后，結合LMD算法對融合信號y(t)濾波降噪處理，從高頻到低頻自適應分解為PF1～PF6和余量u。計算各分量與融合信號的互相關系數，PF2、PF5和PF6分量的相關系數均小于0.1。由頻譜圖分析可知，其頻率成分在15 Hz以下，結合模型有限元分析[11]，認為PF2、PF5和PF6為環境噪聲信號，由剩余分量重構信號z(t)，信號y(t)與z(t)的時程曲線對比見圖9，最后利用RDT+Prony方法進行模態參數識別，并且結合有限元分析結果和穩定圖法[12]剔除識別結果中的虛假模態，識別結構的自振頻率與阻尼比見表3。

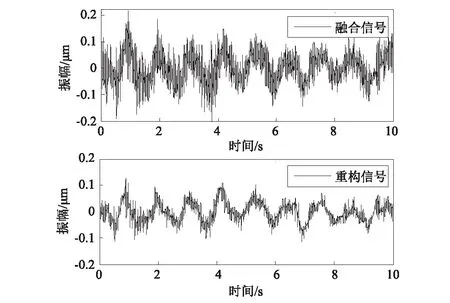
圖9 信號y(t)與z(t)的時程曲線對比Fig.9 The contrast time history curves of signal y(t) and signal z(t)

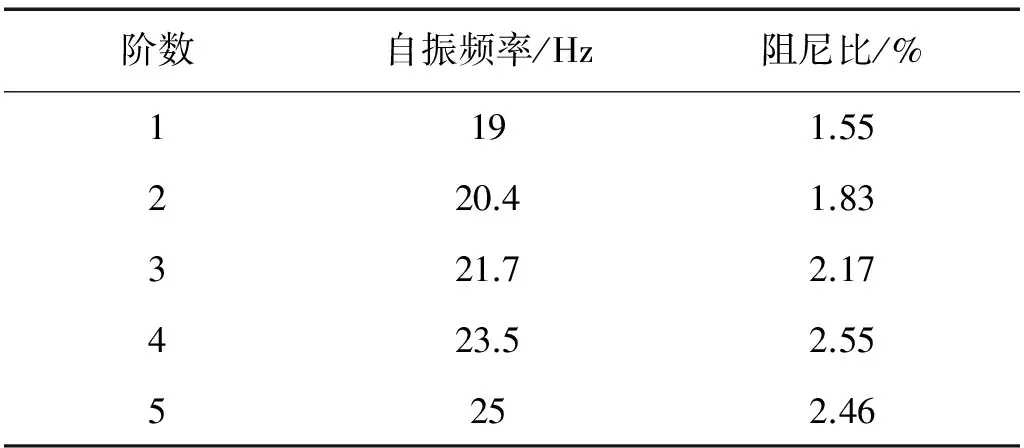
表3 廠房結構模態識別結果

表3中結構整體自振頻率和阻尼比，基本符合工程實際經驗范圍，說明該方法運用于水電站廠房振動測試數據分析中是可行的，且能有效地識別出廠房結構整體動態參數。

5 結 論

本文針對水電站廠房結構振動信號多為低信噪比信號，且單一測點振動信號中結構整體振動信息不完整的特點，研究數據融合和LMD組合動參數識別方法。在反映結構整體振動信息方面，融合信號相較于局部位置的單一測點信號更豐富，信噪比高；LMD在濾除環境噪聲保留有效信息的完整性方面有一定優勢，也能有效地緩解端點效應和減小迭代次數。主要結論如下:

(1)對于互相關性較好的低信噪比信號，該組合方法能有效地提高信息的完整性和融合信號的信噪比。

(2)該組合方法適用于水電站廠房振動測試分析。利用此方法對廠房實測數據進行分析，能準確地提取結構整體振動信息，且結合RDT和Prony方法識別出廠房結構整體模態參數，取得了良好的應用效果。該方法為在強環境噪聲下獲取結構整體動態參數提供一種思路。

[ 1 ] 馬震岳，張運良，陳婧，等.水電站廠房和機組耦合動力學理論及其應用[M]. 北京：中國水利水電出版社，2013.

[ 2 ] 練繼建，王海軍，秦亮.水電站廠房結構研究[M]. 北京：中國水利水電出版社，2007.

[ 3 ] 李火坤，張宇馳，鄧冰梅，等.拱壩多傳感器振動信號的數據級融合方法[J].振動、測試與診斷，2015，35(6)： 1075-1082.

LI Huokun，ZHANG Yuchi，DENG Bingmei ,et al. Study on multi-sensor data-level fusion method of high arch dam vibration signal[J].Journal of Vibration，Measurement &Diagnosis，2015，35(6): 1075-1082.

[ 4 ] 張建偉，江琦，趙瑜，等.一種適用于泄流結構振動分析的信號降噪方法[J].振動與沖擊，2015，34(20): 178-184.

ZHANG Jianwei，JIANG Qi，ZHAO Yu，et al. De-noising method for vibration signal of flood discharge structure[J].Journal of Vibration and Shock，2015，34(20): 178-184.

[ 5 ] 曹沖鋒，楊世錫，楊將新.大型旋轉機械非平穩振動信號的EEMD降噪方法[J].振動與沖擊，2009，28(9)： 33-38.

CAO Chongfeng，YANG Shixi，YANG Jiangxin. De-noising method for non-stationary vibration signals of large rotating machineries based on ensemble empirical mode decomposition [J]. Journal of Vibration and Shock，2009，28(9): 33-38.

[ 6 ] SMITH J S. The local mean decomposition and its application to EEG perception data [J]. Journal of The Royal Society Interface，2005，2(5)： 443-454.

[ 7 ] 程軍圣，張亢，楊宇，等.局部均值分解與經驗模式分解的對比研究[J]. 振動與沖擊，2009，28(5)： 13-16

CHENG Junsheng，ZHANG Kang，YANG Yu，et al. Comparison between the methods of local mean decomposition and empirical mode decomposition [J]. Journal of Vibration and Shock，2009，28(5): 13-16.

[ 8 ] 王婷杰，施惠昌. 一種基于模糊理論的一致性數據融合方法[J]. 傳感器技術，1999,18(6)： 50-53.

WANG Tingjie， SHI Huichang. Consensus data fusion method based on fuzzy theory[J]. Journal of Transducer Technology 1999，18(6)： 50-53.

[ 9 ] 鐘建軍，宋健，由長喜，等.基于信噪比評價的閾值優選小波去噪法[J].清華大學學報(自然科學版)，2014，54(2)： 259-263.

ZHONG Jianjun，SONG Jian，YOU Changxi， et al. Wavelet de-noising method with threshold selection rules based on SNR evaluations[J]. J Tsinghua Univ (Sci & Technol)，2014，54(2)： 259-263.

[10] 卞家磊，朱春梅，蔣章雷，等.LMD-ICA聯合降噪方法在滾動軸承故障診斷中的應用[J].中國機械工程，2016，27(7)： 904-910.

BIAN Jialei，ZHU Chunmei，JIANG Zhanglei，et al.Application of LMD-ICA to fault diagnosis of rolling bearings[J].China Mechanical Engineering，2016，27(7)： 904-910.

[11] 毛柳丹，王海軍.水電站地下廠房結構振動荷載反饋研究[J].水資源與水工程學報，2014，25(3)： 79-82.

MAO Liudan，WANG Haijun. Research on load feedback of structure vibration of underground house of hydropower station[J].Journal of Water Resources & Water Engineering，2014，25(3)： 79-82

[12] 常軍，張啟偉，孫利民.穩定圖方法在隨機子空間識別模態參數中的應用[J].工程力學，2007，24(2)： 39-44.

CHANG Jun，ZHANG Qiwei，SUN Limin. Application of stabilization diagram for modal parameter identification using stochastic subspace method[J].Engineering Mechanics，2007，24(2)： 39-44.