撥開云霧見青天
——探求分式函數“背后”的函數

廈門大學附屬實驗中學 (363123)

林秋林

撥開云霧見青天
——探求分式函數“背后”的函數

廈門大學附屬實驗中學 (363123)

林秋林

事實上，在高中學習中我們碰上的分式函數都是從一些基本的分式函數變形而來，并且我們可以追尋其變形的“足跡”，將其化歸到一些簡單的函數來求解.筆者把每一個分式函數可以化歸到的一個簡單函數稱為這個分式函數“背后”的函數.于是如何找到每一個復雜的分式函數“背后”的函數則成為解決這類問題的關鍵，而它們“背后”的函數其中就包括了如下這兩類基本的分式函數:

圖1 圖2

圖3 圖4

我們可以通過“湊配分離”或“換元分離”的方法，找出分式函數“背后”的函數，再利用它們來解決問題，就可起到事半功倍的作用，即所謂“撥開云霧見青天”.以下我們僅就常見的幾種復雜的分式函數進行分類討論.

一、一次分式函數f(x)=(c≠0,ad≠bc)

圖5

(Ⅰ)若袋中共有10個球，(ⅰ)求白球的個數；(ⅱ)從袋中任意摸出3個球，記得到白球的個數為ξ，求隨機變量ξ的數學期望Eξ.

二、二次分式函數f(x)=(a2+d2≠0)

此類型形式多樣，主要可分為下面幾種情形：

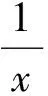
圖6

例6 如圖6,設F1,F2是橢圓3x2+2y2=6的兩個焦點，AB是過焦點F1的一條動弦，試求ΔABF2面積的最大值，并確定取得最大值時弦AB的位置.

令t=2k2+3，則t∈[3,+∞).

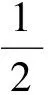
三、復合型分式函數f(x)=(c≠0,ad≠bc)，其中g(x)為非多項式函數

嚴格來說，此類型的函數f(x)不是分式函數，但是我們可以參照解分式函數的思路，利用“湊配分離”的方法，同樣可以通過探求f(x)“背后”的函數來解決此類有關題型.

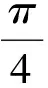
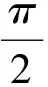
(1)判斷f(x)的奇偶性，并加以證明；

(2)判斷f(x)的單調性，并加以證明；

(3)求f(x)的值域；

本文僅就如何探求分式函數“背后”的函數及其“背后”的函數的作用對一些問題做了具體的分析，筆者希望通過這些例題的“拋磚引玉”，能讓大家都來關注分式函數“背后”的函數的重要性，以期望提高學生們求解分式函數有關題型的能力.