基于AHP和圖論模型的杭州市旅游線路設計研究
葉萌萌+鄒波+王夢其
G20峰會的成功召開,提高了杭州在全國乃至全世界的知名度,杭州旅游業迎來了又一個春天。本文用結合定性與定量的層次分析法,從景色、交通、住宿、餐飲四個方面進行旅游景點的篩選;建立最佳旅游線路的圖論模型,用Dijstra算法求解單源點最短路徑問題,求解最佳旅游線路。
隨著人們生活水平的提高,出門旅游已成為廣泛的娛樂消遣方式。近年來旅游業蓬勃發展,利用相關數據和模型,設計最佳旅游線路,更好地為旅游業服務。G20的成功召開,提高了杭州在全國乃至全世界的知名度,可想而知,未來的杭州將迎來一個旅游熱潮。本文以杭州市旅游景點為例,基于AHP的方法,從景色、交通、住宿、餐飲四個方面進行旅游景點的篩選,用圖論模型里的貪婪算法進行最佳線路設計,為游客游覽杭州提供參考依據。
一、基于AHP的景點篩選
人們出游時由于時間和經費的限制,很難走遍所有的景點,而大大小小的景點如何選擇也很是讓人頭疼。AHP(層次分析法)是20世紀70年代中期,由美國運籌學家托馬斯﹒塞蒂(T﹒L﹒Saaty)正式提出的,是一種結合定性與定量分析的一種決策方法。
第一步:根據各種旅游網站搜索量和杭州景點排名,挑選出排名前8的景點,篩選的層次結構模型圖如圖1。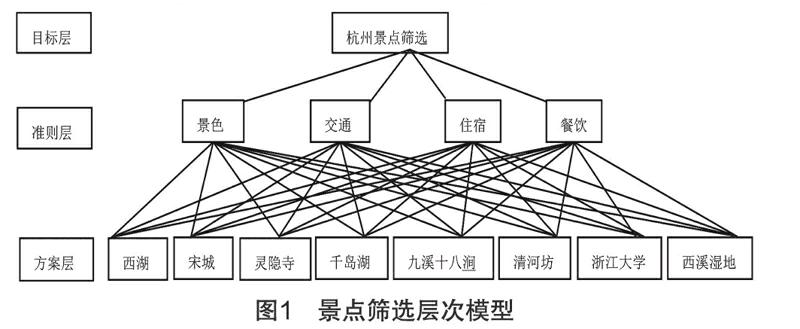
第二步:依據1-9標度法,對準則層和方案層構造判斷矩陣A、Bj( j=1…4),其中A是關于景色、交通、住宿、餐飲的判斷矩陣(見公式1),Bj是八個景點對準則層第j個因素的判斷矩陣。
(1)
第三步:根據判斷矩陣,用matlab求得對應的特征根λ,λj( j=1…4)、特征向量,并對求出的特征向量歸一化得到ω,
ωj( j=1…4)。
第四步:計算景點對準則層的組合權值和景點對目標層的權值,如表1。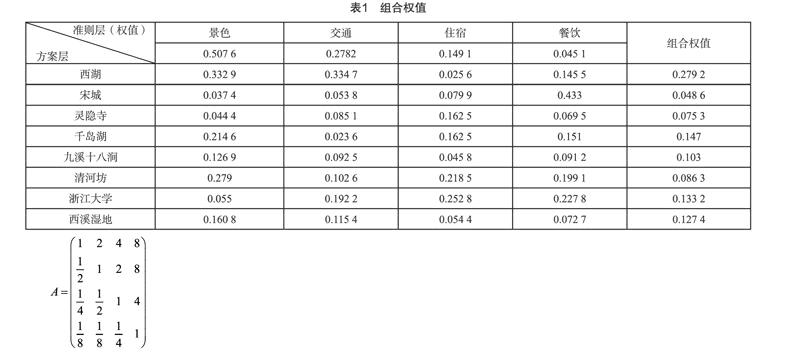
根據總目標權值表選取排名前五也是權值大于0.1的景點為需要游覽的景點,分別是西湖、千島湖、九溪十八澗、浙江大學、西溪濕地。
二、基于圖論的最佳線路設計
關于線路設計的圖論問題,首先將地圖上的景點繪制成由點和線組成的關系圖,考慮方向和數量則變成加權有向圖。Hamiltun路最短路徑問題的解決算法很多,貪婪算法方法簡單,程序容易實現。而Dijstra算法正是利用貪心算法求解單源點最短路徑問題最常用的方法。
本文最佳旅行線路要考慮景點不重復、費用最省。對于選中的五個景點,我們考慮從其中一個景點出發,每個景點有且僅游覽一遍回到出發景點,不同線路的交通費不一樣,以交通費用作
為圖的頂點和邊長的權值,構造有向加權圖,用Dijstra算法求得最佳旅游線路為西湖→浙江大學→西溪濕地→九溪十八澗→千島湖→西湖。
這五個景點的住宿費用通過飛豬網,對同一家經濟型酒店如家酒店的價格對比可知:西湖>西溪濕地>九溪十八澗>浙大>千島湖。根據五個景點的最佳游覽時間總和可知,最佳旅游天數是3天,而5個地方的景點住宿標準差異較大,結合上面求得的線路和選擇兩個地點住宿,最終確定游覽線路與上圖一致,西湖游覽時間放在千島湖回來,住宿地址確定為九溪十八澗和千島湖各一晚。
三、結語
本文在調查杭州景點及其周邊信息的基礎上,考慮時間和金錢的限制,用層次分析法對杭州的景點進了篩選,從景色、交通、住宿、餐飲四個方面考慮,最終選出了西湖、千島湖、九溪十八澗、浙江大學、西溪濕地5個景點。對于選出來的景點,查詢了景點間的交通費用作為無向圖的邊長信息,把問題轉化為單源點最短路徑問題,用Dijstra算法求得最佳旅游線路為西湖→浙江大學→西溪濕地→九溪十八澗→千島湖→西湖。其方法可推廣用于其他城市景點的線路規劃,為旅行社和個人游提供線路參考和節約旅游成本。
(作者單位:浙江經濟職業技術學院)endprint

