珠聯璧合，正、余弦定理解三角形

■河南省許昌高級中學 胡銀偉

珠聯璧合，正、余弦定理解三角形

■河南省許昌高級中學 胡銀偉

正、余弦定理將三角形的邊和角有機地聯系起來,從而使三角與幾何產生聯系,為求與三角形有關的量(如面積,其外接圓、內切圓的半徑和面積等)提供了理論依據,也是判斷三角形形狀、證明三角形中有關等式的重要依據。

在利用正、余弦定理解三角形時,如果式子中含有角的余弦或邊的二次式,要考慮用余弦定理;如果式子中含有角的正弦或邊的一次式時,則考慮用正弦定理;以上特征都不明顯時,則兩個定理要珠聯璧合,有可能都會用到。

一、求三角形的基本量

解析:設△ABC的內角∠BAC,B,C所對邊的長分別是a,b,c。

由余弦定理得:

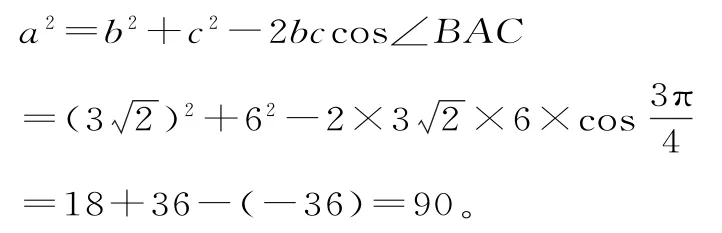
在△ABD中,因為AD=BD,所以∠ABD=∠BAD,所以∠ADB=π-2B。

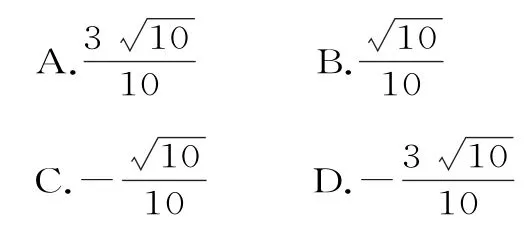
解法一:設△ABC中角A,B,C所對的邊分別為a,b,c。

由余弦定理得b2=a2+c2-2accosB=所以b=

解法二:同法一得由正弦定理得sinC=sinA,又B=所以sinC=即cosA+故tanA=-3,A為鈍角。

又因為1+tan2A=所以cos2A=故選C。

(2016·四川卷)在△ABC中,角A,B,C所對的邊分別是a,b,c,且

(1)證明:sinAsinB=sinC;

(2)若b2+c2-a2=求tanB。

解析:(1)根據正弦定理,可設則a=ksinA,b=ksinB,c=ksinC。

變形可得sinAsinB=sinAcosB+cosAsinB=sin(A+B)。

在△ABC中,根據A+B+C=π,有sin(A+B)=sin(π-C)=sinC。

所以sinAsinB=sinC。

(2)由已知,b2+c2-a2=根據余弦定理,有

由(1)知,sinAsinB=sinAcosB+cosAsinB,所以

點評:利用正、余弦定理解題是歷年高考的熱點,也是必考點,求解的關鍵是合理應用正、余弦定理實現邊角的互化。其中正弦定理是一個連比等式,只要知道其比值或等量關系就可以運用正弦定理通過約分達到解決問題的目的。運用余弦定理時,要注意整體思想的運用。

二、解與三角形的面積有關的問題

△ABC中,角A,B,C的對邊分別為a,b,c,若△ABC的面積S=(b+c)2-a2,則sinA=

解:由余弦定理得cosb2+c2-a2=2bccosA。

S=(b+c)2-a2=b2+c2-a2+2bc=2bc(cosA+1)。

在△ABC中,a,b,c分別為內角A,B,C的對邊,且asinB=-b·

(1)求A;

解:(1)因為asin所以由正弦定理得

故a2=b2+c2-2bccosA=7c2,則a=由正弦定理得sin

點評:正弦定理和余弦定理并不是孤立的,解題時要根據具體題目合理選用,有時還需要交替使用。應用時要注意化角法、化邊法、面積法、初等幾何法等方法的靈活運用,也要注意體會其中蘊含的函數與方程思想、等價轉化思想及分類討論思想。

三、正、余弦定理與三角問題的綜合應用

(2)在△ABC中,角A,B,C的對邊分別為a,b,c,滿足c=3,f(C)=0且sinB=2sinA,求a,b的值。

解:(1)f(x)=

因為sinB=2sinA,所以b=2a。

因為c2=a2+b2-2abcosC,所以

(2015·全國課標Ⅰ)在平面四邊形ABCD中,∠A=∠B=∠C=75°,BC=2,則AB的取值范圍是

解法一:如圖1所示。

過點C作CE∥AD交AB于點E,則∠CEB=75°,CE=BC=2,∠BCE=30°。

圖1

所以BE2=BC2+CE2-2BC·CE·cos∠BCE=4+4-8×此時,BE=

延長CD交BA的延長線于點F,則△BCF為等腰三角形,且∠CFB=30°,FC=FB。

由題意可知,6-2＜AB＜6+2。

解法二:如圖2所示,延長BA、CD交于點E。

在△ADE中,∠DAE=105°,∠ADE=45°,∠E=30°。

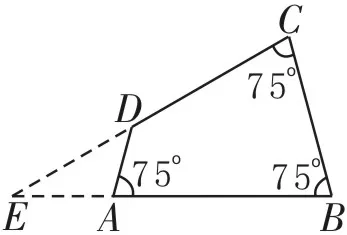
圖2

點評:關于解三角形問題,一般要用到三角形的內角和定理,正、余弦定理及有關三角形的性質,常見的三角變換方法和原則都適用,同時要注意“三統一”,即“統一角、統一函數、統一結構”,這是使問題獲得解決的突破口。此外,在解三角形時,還要注意三角形內角和定理對角的范圍的限制。如例7,解法一是借助幾何圖形分析極端情況,得到AB邊的取值范圍;解法二則是借助兩個定理建立函數關系,通過代數方法進行求解。

(責任編輯 徐利杰)