數列綜合拔高訓練（B卷）答案與提示

數列綜合拔高訓練（B卷）答案與提示

1.B 2.D 3.C 4.C 5.B 6.B 7.C 8.C

9.C 提示:因為a4=2所以則

11.D 提示:設七人錢數組成的等差數列的公差為d,七人的錢數依次為a-3d,a-2d,a-d,a,a+d,a+2d,a+3d,由題意可得解得a=101,d=-7。則丙的錢數為a-d=108。

12.B

13.A

14.C 提示:依題意得an+1=an+a1,即an+1-an=a1=2,所以數列{an}是首項為2,公差為2的等差數列,an=2+2(n-1)=2n,

15.A 提示:當n=1時,a1=S1=0,當n≥2時,an=Sn-Sn-1=2n-2,n=1時上式也成立,綜上,an=2n-2。又T2015=-a2+a4-a6+a8+…+(-a2010+a2012)+a2014

16.B 提示:因為an+1+(-1)nan=2n-1,所以a2-a1=1,a3+a2=3,a4-a3=5,a5+a4=7,a6-a5=9,a7+a6=11,…,a11+a10=19,a12-a11=21。因此,a1+a3=2,a4+a2=8,…,a12+a10=40,從第一項開始,依次取2個相鄰奇數項的和都等于2,從第二項開始,依次取2個相鄰偶數項的和構成首項為8,公差為16的等差數列,以上式子相加可得,S12=a1+a2+…+a12=(a1+a3)+(a5+a7)+(a9+a11)+(a2+a4)+(a6+a8)+(a10+a12)=3×2+8+24+40=78。

17.B 提示:因為無窮數列{an}和{bn}都是等差數列,其公差分別為k和h,且數列{anbn}也是等差數列,所以2a2b2=a1b1+a3b3,即2(a1+k)(b1+h)=a1b1+(a1+2k)(b1+2h),整理得2a1b1+2a1h+2b1k+2kh=2a1b1+2a1h+2b1k+4hk,即hk=0。

18.B 提示:設鈍角三角形的三內角為60°-α,60°,60°+α,則90°＜60°+α,且60°-α＞0,故有30°＜α＜60°。設60°+α對應a邊,60°-α對應b邊,由正弦定理得,m,所以

19.D 提示:因為等差數列{an}的前n項和為Sn,數列{Sn}有唯一的最大項S3,所以公差d＜0,a1＞0,a2＞0,a3＞0,a4＜0。

A.由S5=5a3＞0,S6=3(a3+a4)與0的大小關系不確定,可知A不正確;

B.H5=S1+2S2+3S3+4S4+5S5＞0,H6=S1+2S2+3S3+4S4+5S5+6S6,由選項A的分析可知S6=3(a3+a4)與0的大小關系不確定,H5·H6與0的大小關系也不確定,因此不正確;

C.數列{an}是單調遞減數列,而數列{Sn}在n≤3時單調遞增,n≥4時單調遞減;

D.若a3+a4＞0,則S6＞0,而S7=7a4＜0,因此H6有可能是數列{Hn}的最大項。

20.D 提示:由等差數列的性質及a5=得,a1+a9=a2+a8=a3+a7=a4+a6=2a5=π,f(a5)=1。

因為f(x)=sin2x+cosx+1,所以f(a1)+f(a9)=sin2a1+cosa1+1+sin2a9+cosa2+1=2。

同理,f(a2)+f(a8)=f(a3)+f(a7)=f(a4)+f(a6)=2,故{yn}的前9項和是9。

21.D 22.C 23.B 24.C 25.B 26.D 27.C 28.D 29.B 30.C 31.A

32.-1 33.210 提示:由等差數列性質可知,Sm,S2m-Sm,S3m-S2m成等差數列,則S3m=210。

34.an=2n-1 提示:由anan+1=4Sn-1(n∈N*)得,an-1an=4Sn-1-1,故anan+1-an-1an=4an,an+1-an-1=4。當n=1時,可得a2=3。由an+1-an-1=4可知數列{an}的奇數項和偶數項分別為等差數列,公差均為4,首項分別為1,3,所以當n=2k-1(k∈N*)時,an=a2k-1=1+4(k-1)=4k-3=2n-1;當n=2k(k∈N*)時,an=a2k=3+4(k-1)=2n-1,故an=2n-1。

35.2016 提示:在等差數列{an}中,由S3=2a3知,3a2=2a3,而S5=15,則a3=3,于是a2=2,從而其公差為1,首項為1,因此an=n,故a2016=2016。

36.15 提示:由于S9=9a5,所以a5=2,故a5+an-4=32,Sn=所以n=15。

37.4 提示:由題意得(a1+2d)2=a1·(a1+12d),把a1=1代入式子可得d=2或0(舍去),則an=a1+(n-1)d=2n-1,Sn=由對勾函數y=的性質知,當n+1=3?n=2時,n+1+取得最小值6,則的最小值為4。

39.②③ 提示:由(a2-1)3+2010(a2-1)=1,(a2009-1)3+2010(a2009-1)=-1,可得a2-1＞0,-1＜a2009-1＜0,即a2＞1,0＜a2009＜1,從而可得等差數列的公差d＜0,a2009＜a2,③正確。

把已知的兩式相加可得(a2-1)3+2010(a2-1)+(a2009-1)3+2010(a2009-1)=0。

整理可得(a2+a2009-2)·[(a2-1)2+(a2009-1)2-(a2-1)(a2009-1)+2010]=0。

結合上面的判斷可知(a2-1)2+(a2009-1)2-(a2-1)(a2009-1)+2010＞0。

所以a2+a2009=2,S2010=2010,②正確。

由于d＜0,a2010＜a2009＜1,則S2009=S2010-a2010=2010-a2010＞2009,①錯誤。

由公差d＜0,可得a2+a2008＞a2+a2009＞a2+a2010,結合等差數性質,可得2a1005＞2＞2a1006,即0＜a1006＜1＜a1005。

④S2009-S2=a3+a4+…+a2009=2007a1006＞0,故④錯誤。

42.470 提示:由題意得an=n2cos當n分別取1,2,3,4,5,6,…時,cos分別取故S30=

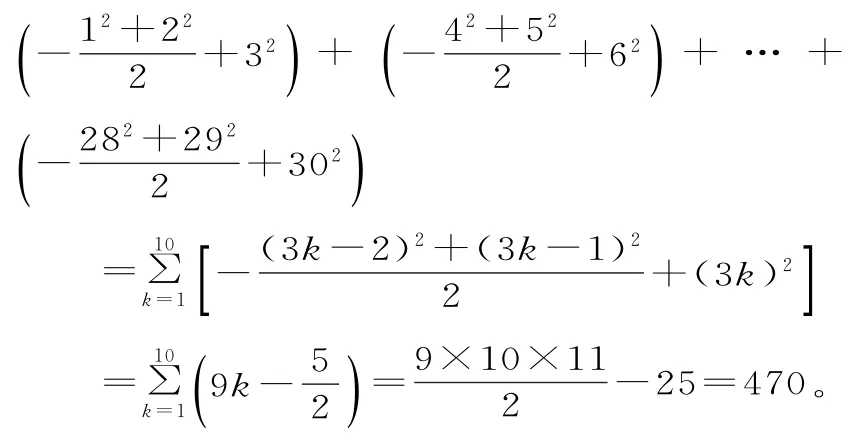
49.(1)an=2n-7(n∈N*)。

(2)由an=2n-7＜0,得即n≤3,所以當n≤3時,an＜0,當n≥4時,an＞0。

易知Sn=n2-6n,S3=-9,S5=-5。

所以T5=-(a1+a2+a3)+a4+a5=-S3+(S5-S3)=S5-2S3=13。

當n≤3時,Tn=-Sn=6n-n2;

當n≥4時,Tn=-S3+(Sn-S3)=Sn-2S3=n2-6n+18。

50.(1)由an+2=2an+1-an+2,得bn+1-bn=an+2-2an+1+an=2。

因此,{bn}是首項為1,公差為2的等差數列。

(2)由(1)得bn=2n-1,于是an+1-an=2n-1。因此,當n≥2時,an=

(a2-a1)+(a3-a2)+…+(an-an-1)[]+a1

=1+3+…+(2n-3)[]+1

=(n-1)2+1。a1=1,因此當n=1時也滿足上式,

故{an}的通項公式an=(n-1)2+1。

51.(1)由題意知(2a1+d)(3a1+3d)=36,將a1=1代入上式解得d=2或d=-5。因d＞0,故d=2,解得Sn=n2(n∈N*)。

(2)由(1)的結論可得am+am+1+am+2+…+am+k=(2m+k-1)·(k+1),所以(2m+k-1)(k+1)=65。

由m,k∈N*知2m+k-1＞k+1＞1,故所以

52.(1)由題設知:

anan+1=λSn-1,an+1an+2=λSn+1-1。

兩式相減得an+1(an+2-an)=λan+1。

因為an+1≠0,所以an+2-an=λ。

(2)由題意知a1=1,a1a2=λS1-1,可得a2=λ-1,由(1)知,a3=λ+1。

若{an}為等差數列,則2a2=a1+a3,解得λ=4,故an+2-an=4。

由此可得{a2n-1}是首項為1,公差為4的等差數列,a2n-1=4n-3;

{a2n}是首項為3,公差為4的等差數列,a2n=4n-1。

所以an=2n-1,an+1-an=2,存在λ=4,使得數列{an}為等差數列。

53.(1)當n=1時,S1=2a1-4,a1=4。

當n≥2時,an=Sn-Sn-1=2an-2n+1-2an-1+2n,故an-2an-1=2n,即1,bn-bn-1=1(常數)。

(2)由dn+1＞dn得4n+1+(-1)nλ·2n+2＞4n+(-1)n-1λ·2n+1,即3·4n+(-1)n·λ·2n+2+(-1)nλ·2n+1＞0。

3·4n+(-1)nλ·2n+1×3＞0。

整理得2n-1+(-1)nλ＞0。

當n為奇數時,λ＜2n-1,則λ＜1;

當n為偶數時,λ＞-2n-1,則λ＞-2。

所以-2＜λ＜1。

又λ為非零整數,故λ=-1。

x1+x2=1。

(2)由(1)知,當x1+x2=1時,有f(x1)+f(x2)=1,則:

(3)當n=1時,T1=a1=S2+1=由T1＜λ(S2+1),得λ＞

55.(1)證明過程略。(2)證明過程略。

57.(1)an=n。

(2)Tn=(n-1)·2n+2

58.(1)bn=3n-1。

(2)c1+c2+…+c2015+c2016=32016。

59.(1)證明過程略。

編者的話:同學們在演練的過程中,如果需要更為詳細的參考答案,請掃描右邊的二維碼,關注編輯部的官微“高中數學解題反思”,不但能獲悉詳細參考答案,還可以另辟蹊徑,開拓知識視野,學會解題反思!

(責任編輯 徐利杰)