呈現出題脈絡 破解思維難題
——以“函數與幾何綜合題”為例

□駱金 何娜

（杭州啟正中學，浙江杭州 310003；杭州大成岳家灣實驗學校，浙江杭州 310003）

呈現出題脈絡 破解思維難題
——以“函數與幾何綜合題”為例

□駱金 何娜

（杭州啟正中學，浙江杭州 310003；杭州大成岳家灣實驗學校，浙江杭州 310003）

為減輕學生的解題負擔，教師可以從研究題目的編制規律入手，揭示解題的基本思想和方法，并且讓學生共同參與編題與解題的全過程，有助于學生打開思維的脈絡，體味主動學習的樂趣，變“要我解”為“我要解”.

脈絡；思維；生題

在各地的數學中考試卷中，函數與幾何相結合的綜合題頻繁出現.這類題是考查學生靈活運用初中階段所學知識來分析和解決問題的一個重要手段和方法.但對初中學生來說難度頗高，它不僅要求學生溝通題目中自變量、函數在幾何圖形中所表示的量之間的關系，而且要求學生會運用“函數與方程”“數形結合”“分類討論”等數學思想解決問題.在以往的教學中教師往往要求學生解大量此類題目，以期達到理解掌握的目的.但學生解完后還是一臉疑惑，不知道來龍去脈.能否從破解題目編制的奧秘入手，讓學生通曉并掌握解決此類問題的基本思想和方法？為此，本文將重點探索此類題目的編制脈絡，并從三個方向，即“順向”“逆向”和“縱向”展開研究，繪制出題目“生長”的線路圖（如圖1所示）.

一、順向“生題”

順向“生題”，就是已知函數的解析式，求內接幾何圖形與函數的交點坐標，繼而可求內接圖形的邊長、周長和面積等.

因為函數的解析式已知，也就是函數圖象上一點的橫縱坐標之間的一個等量關系已知，所以只要再另添一個橫縱坐標之間的等量關系，就可求得該點的坐標.而添加的這個關系可以直接用“數”（方程）的形式給出，也可以利用“形”（幾何圖形中隱含著線段之間的數量關系）間接獲取.以下舉例說明.

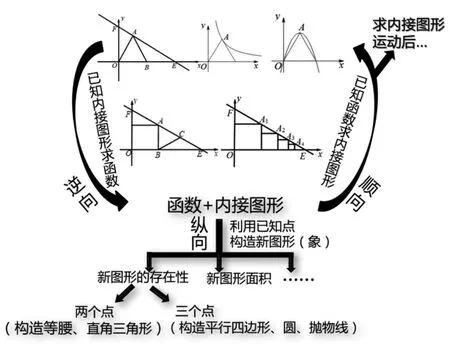
圖1

此時增加最直接的條件是已知點A的橫坐標或縱坐標，但間接地只要已知點A的橫坐標與縱坐標的等量關系.而這個關系可以借助函數的內接幾何圖形給出.所以點A是連接函數與其內接幾何圖形的媒介.

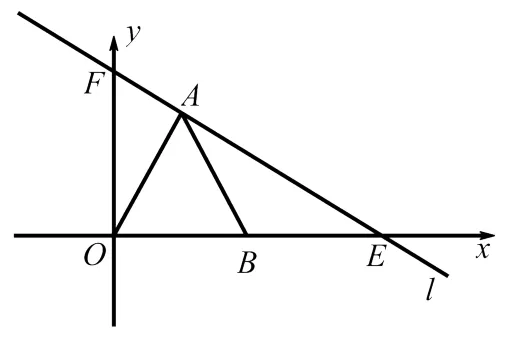
圖2

如圖2，我們可以放入等邊三角形OAB，其中點B在x軸上，點A在l上.此時若設點A的橫坐標為m，則其縱坐標就為m，因為點A在函數的圖象上，所以，解 得 m=1，所 以 點.繼而可求得△OAB的邊長、周長、面積等.

（一）換圖

我們可改變內接幾何圖形的形狀，將等邊三角形改換成等腰直角三角形、正方形、半圓、正多邊形（如圖3）等.

圖3

（二）換線

我們還可以改變函數的類型，將一次函數改換成反比例函數（圖4）和二次函數（圖5）等.

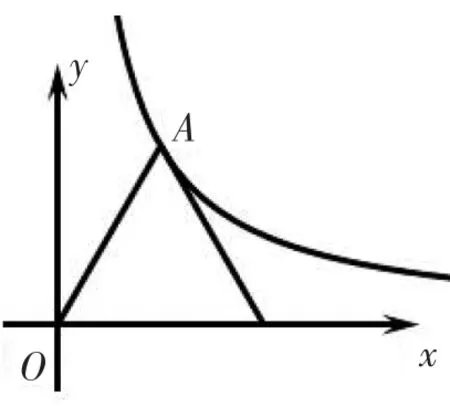
圖4

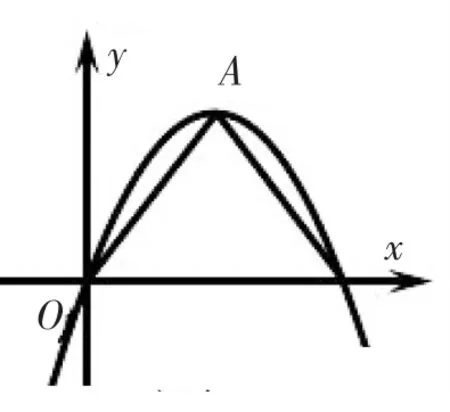
圖5

（三）增加個數

內接圖形的個數也可以從一個變成多個.如圖6、圖7.

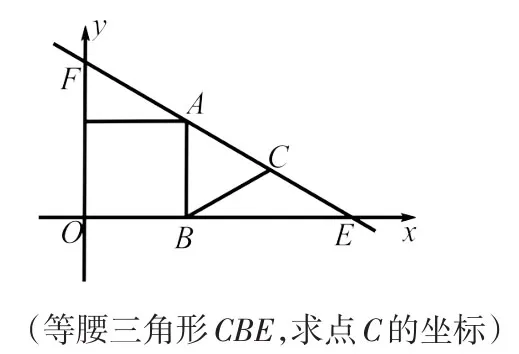
圖6

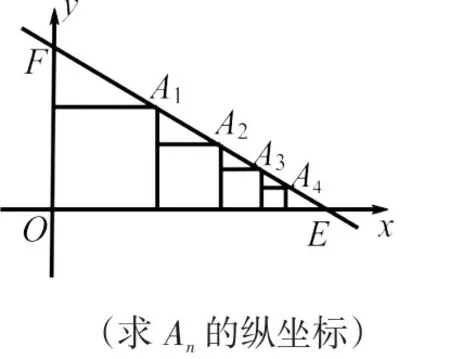
圖7

通過換圖、換線讓學生明白解題的突破點仍然是幾何圖形與函數圖象的交點，至于增加個數則只需將交點逐個依序擊破即可.

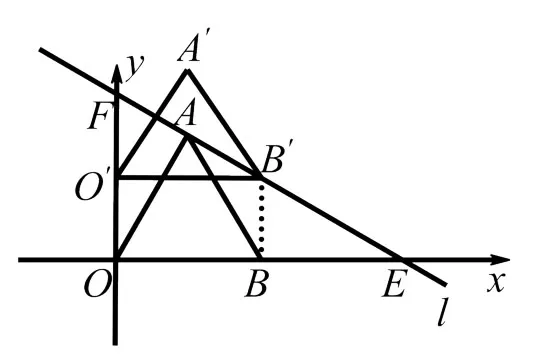
圖8

（四）圖形運動

我們可以對給定的幾何圖形（或其一部分）施行平移、翻折和旋轉的位置變化，然后分析新的圖形與函數圖象之間的關系.

如對于前述的一次函數和內接等邊三角形OAB，我們可以作如下的運動變換：

①如圖8，將△OAB沿y軸平移到△O'A'B'，使點B'在直線l上，問平移的距離是多少？

②如圖2，求△OAB關于直線l的對稱三角形的頂點坐標.

解決此類問題只需將圖形變換帶來的“不變”特征定量地反映到點的坐標上.

二、逆向“生題”

逆向“生題”，就是已知內接圖形的邊長或半徑等，求函數解析式.

求函數的解析式也就是求解析式中的待定系數，而確定系數的條件可以直接給出圖象上點的坐標.但為了增加思維的含金量，我們可以嵌入內接幾何圖形，通過數形結合間接地求出點的坐標.以下舉例說明.

三、縱向“生題”

縱向“生題”，就是利用函數圖象或內接幾何圖形中的點，構造出新的圖形或圖象.

我們可以選取圖象或內接幾何圖形中的某些點來構造新的幾何圖形，如三角形、四邊形、圓等，并可進一步求這些新幾何圖形的某些量或新舊幾何圖形之間的關系.又可以探索新圖形的存在性問題等.還可以利用它們來構造新的函數，如一次、二次、反比例函數等，從而創新生成千姿百態的函數與幾何綜合問題.以下舉例說明.

如對于前面圖2中所述的一次函數和內接等邊三角形OAB，我們可以“取點”繼續進行編題：

（一）構新圖

③如圖2，若以A，O，E，Q為頂點的四邊形是平行四邊形，求點Q的坐標；A，O，E三點坐標可求，此時點Q的位置有三種可能，求得Q點坐標為

④如圖2，是否存在以BE為邊的等腰三角形BEM，使得點M在直線l上？若存在，試求點M的坐標.

BE可以作為腰，也可以是底，因而點M的位置有四種可能.可求得點M坐標為：

⑤如圖2，在直線EF上有一動點M，在坐標系內有另外一點N，若以點O，F，M，N為頂點構成的四邊形為菱形，則滿足這樣的點N的個數為（ ）

A.3個 B.4個 C.5個 D.6個

因為此時OF=FM或OM=FM，所以點N的位置有4種可能，選B.

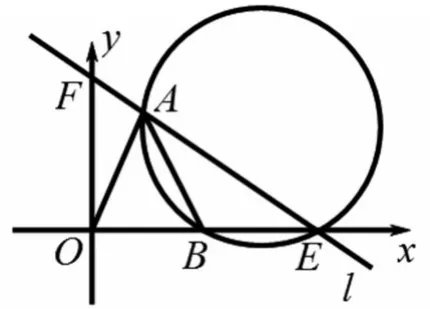
圖9

⑥如圖9，過A，B，E三點畫圓，將此圓如何平移才能與x軸和y軸同時相切；有四種移法：向上平移2-個單位，再向左平移1個單位；或向下平移2+個單位，再向左平移1個單位；或向上平移2-個單位，再向左平移5個單位；或向下平移2+個單位，再向左平移5個單位.

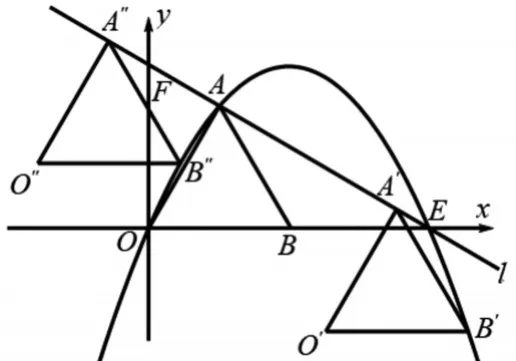
圖10

⑦如圖10，過A、O、E三點畫拋物線，將△OAB沿直線l的方向平移到△O'A'B'，使得點B'在拋物線上，問平移的距離是多少？

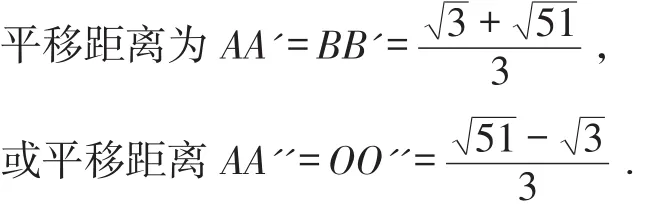
（二）求面積

⑧在直線l上是否存在點P，使得△PAB的面積是△OAB面積的一半？

⑨若點P是⑦中求出的拋物線AE段上一動點（不與A，E重合），設四邊形OAPE的面積為S，求S的最大值.

綜上，從研究題目的編制規律入手，讓學生參與教學的全過程，就能從根本上減輕學生的解題負擔．并且在教學中我們完全可以讓學生沿著這樣的脈絡自己編題，自己解題，從而體味主動學習的樂趣，變“要我解”為“我要解”.