清風和雨 綿綿悠長
——2017年高考數(shù)學文化試題感悟

● (英雄山中學,山東 泰安 271000)

2017-08-01

尹承利(1963-)，男，山東泰安人，中學高級教師.研究方向數(shù)學教育.

清風和雨綿綿悠長
——2017年高考數(shù)學文化試題感悟

●尹承利
(英雄山中學,山東 泰安 271000)

教育部考試中心下發(fā)的《關(guān)于2017年普通高考考試大綱修訂內(nèi)容的通知》(教試中心函(2016)179號)，公布了2017年各學科高考大綱的主要修訂內(nèi)容，在數(shù)學考綱的修改部分，特別強調(diào)了要對數(shù)學文化進行考查.“數(shù)學文化怎樣考”成為中學數(shù)學界熱議和期待的話題，2017年高考對“數(shù)學文化”的考查是以怎樣的面目呈現(xiàn)的？文章就此作一些賞析和感悟.

高考;數(shù)學文化;感悟

2017年高考對“數(shù)學文化”的考查，雖然沒有呈現(xiàn)出人們預期的“驟風大作”的氣勢，倒也“清風和雨”潤人心田.在高考試題中滲透數(shù)學文化成為2017年數(shù)學高考“可圈可點”的一大亮點，全國卷Ⅰ、卷Ⅱ和高考改革地區(qū)的浙江卷都作了有益的嘗試與探索，體現(xiàn)了高考“增加數(shù)學文化”的要求.

1 試題賞析

例1我國古代數(shù)學名著《算法統(tǒng)宗》中有如下問題：“遠望巍巍塔七層，紅光點點倍加增；共燈三百八十一，請問尖頭幾盞燈？”意思是：一座7層塔共掛了381盞燈，且相鄰兩層中的下一層燈數(shù)是上一層燈數(shù)的2倍，則塔的頂層共有燈

( )

A.1盞 B.3盞 C.5盞 D.9盞

(2017年全國數(shù)學高考卷Ⅱ理科試題第3題)

分析可設(shè)最頂層燈塔所掛燈數(shù)為a，則第2層為2a，第3層為4a，…,第7層為64a.本題實質(zhì)是考查等比數(shù)列求和公式，從而127a=381，可得a=3.故選B.

評注我國古代數(shù)學有著極其輝煌的成就，出現(xiàn)過劉徽、祖沖之、秦九韶、楊輝等偉大的數(shù)學家，以及《九章算術(shù)》、《數(shù)書九章》、《算數(shù)書》、祖暅原理等數(shù)學名著和名題.以這些名著、名題為試題背景，可以引導我們理解數(shù)學，感受數(shù)學家的崇高品質(zhì)及探究、解決數(shù)學問題的過程，進而體會中國古代數(shù)學的偉大貢獻，增強愛國主義情懷.程大位是我國明代偉大的數(shù)學家，被譽為“珠算之父”，他的應用數(shù)學巨著《算法統(tǒng)宗》的問世，標志著我國的算法由籌算到珠算轉(zhuǎn)變的完成.程大位在《算法統(tǒng)宗》中常以詩歌的形式呈現(xiàn)數(shù)學問題，體現(xiàn)了數(shù)學的“文化美”.

例2我國古代數(shù)學家劉徽創(chuàng)立的“割圓術(shù)”可以估算圓周率π，理論上能把π的值計算到任意精度.祖沖之繼承并發(fā)展了“割圓術(shù)”，將π的值精確到小數(shù)點后7位，其結(jié)果領(lǐng)先世界一千多年.“割圓術(shù)”的第一步是計算單位圓內(nèi)接正六邊形的面積S6，S6=________.

(2017年浙江省數(shù)學高考試題第11題)

分析將正六邊形分割為6個等邊三角形，則

評注割圓術(shù)是我國古代數(shù)學家劉徽創(chuàng)造的一種求周長和面積的方法：隨著圓內(nèi)接正多邊形邊數(shù)的增加，它的周長和面積越來越接近于圓周長和圓面積，“割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體，而無所失矣”．劉徽就是大膽地應用了以直代曲、無限趨近的思想方法求出了圓周率π的近似值.說到圓周率π，自然想到我們引以為豪的“徽率”和“祖率”，它的歷史饒有趣味,我國古代數(shù)學家對圓周率方面的研究工作，成績十分地突出.本題所介紹的祖沖之研究圓周率π的成果，讓我們感到無比自豪和驕傲，古代科學家在艱難的環(huán)境中研究科學的無私精神和崇高品質(zhì)，值得我們尊敬和學習.

例3如圖1，正方形ABCD內(nèi)的圖形來自中國古代的太極圖，正方形內(nèi)切圓中的黑色部分和白色部分關(guān)于正方形的中心成中心對稱.在正方形內(nèi)隨機取一點，則此點取自黑色部分的概率是

( )

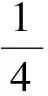
(2017年全國數(shù)學高考卷Ⅰ文科試題第2題)

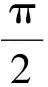
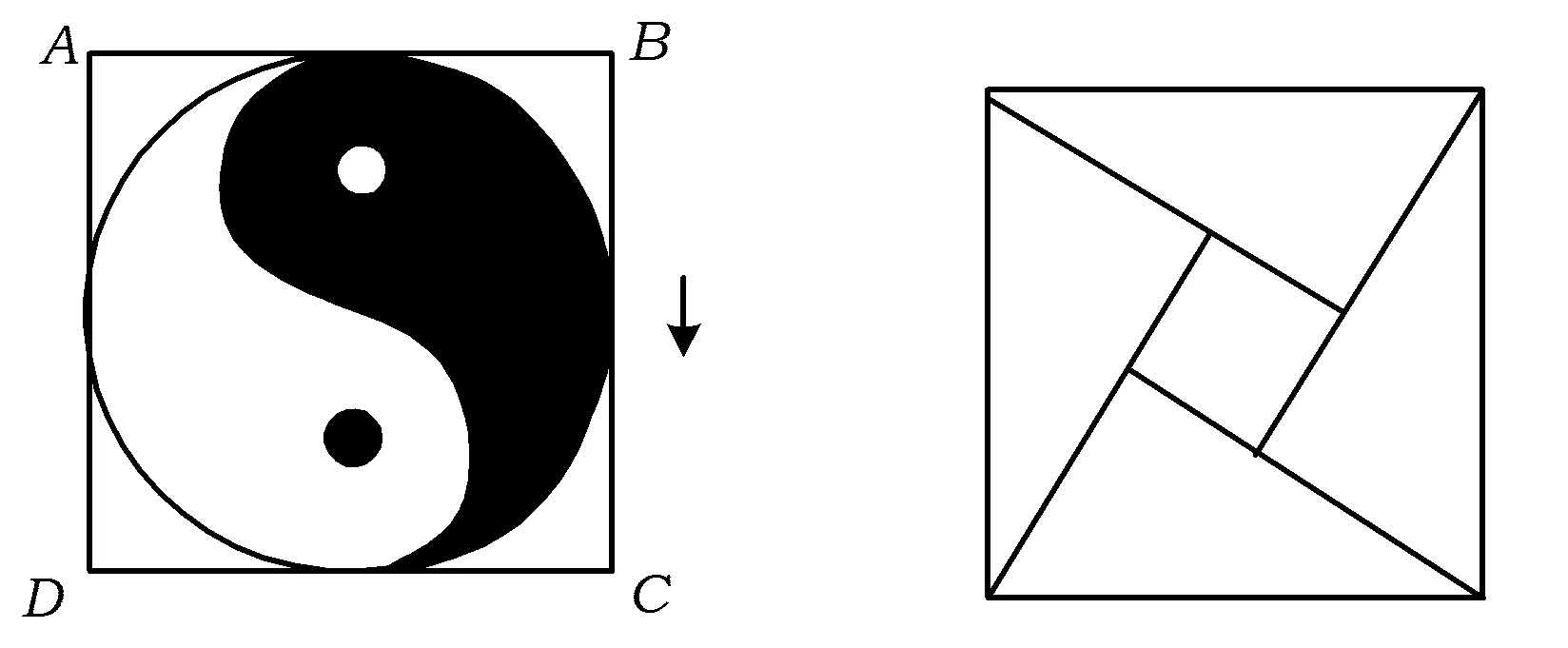
圖1 圖2

評注在我國傳統(tǒng)文化中有很多體現(xiàn)“數(shù)學美”的圖形.如本題所示的太極圖是由黑白兩個魚形紋組成的圓形圖案，充分體現(xiàn)了相互轉(zhuǎn)化、對稱統(tǒng)一的形式美、和諧美.還有像莊重大氣的2002年北京國際數(shù)學家大會的會標，它是以“趙爽弦圖”為基礎(chǔ)設(shè)計的.勾股定理是刻畫直角三角形特征的一條重要定理，它的發(fā)現(xiàn)、驗證、應用蘊含著豐富的文化價值，最早對勾股定理進行證明的是1700多年前的漢代數(shù)學家趙爽，他繪制了極富創(chuàng)意的弦圖，后人稱之為“趙爽弦圖”(圖2)，采用“出入相補”原理使得勾股定理不證自明.以“弦圖”為基本圖形，定理的證明體現(xiàn)了“形數(shù)統(tǒng)一”的思想方法，具有科學創(chuàng)新的重大意義.我國數(shù)學文化中蘊含著豐富的寶藏，值得我們?nèi)ド钊胪诰?

2 3點感悟

2.1 高考試題體現(xiàn)了“3個滲透”

數(shù)學文化的最主要內(nèi)涵是一種理性思維方式在實踐過程中的不斷探索，形成的數(shù)學史、數(shù)學精神及其應用[1].2017年的高考“數(shù)學文化”試題基本體現(xiàn)出了“3個滲透”——滲透數(shù)學史料、滲透數(shù)學精神、滲透數(shù)學應用.上述3個高考試題所滲透的數(shù)學史料，讓我們自然而然地接受了“數(shù)學文化”的熏陶；古代數(shù)學家劉徽、祖沖之及祖暅在艱難困苦的環(huán)境中研究科學的數(shù)學精神值得我們學習和敬仰，也更增加了我們的愛國情懷；我國古代數(shù)學遵循“經(jīng)世濟用”，涉及的研究大多與實際生活、生產(chǎn)結(jié)合緊密，具有濃厚的實際背景，無論是例1還是例2都充分說明了這一點.

2.2 高考試題起到了導向作用

數(shù)學文化是數(shù)學學科的一個有機組成部分，有著非常豐富的內(nèi)涵和外延.了解數(shù)學文化，有利于激發(fā)學生對于數(shù)學學習的欲望和興趣.在高考試題中滲透數(shù)學文化，可以適當引導中學數(shù)學的教學，使得更多的教師關(guān)注數(shù)學文化，研究數(shù)學文化，將數(shù)學的本質(zhì)教授給學生.學生通過數(shù)學文化的熏陶，可以促進對健全人格的養(yǎng)成.一方面，可以學到了數(shù)學家們那種不畏艱辛、不怕失敗的精神；另一方面，又能學到以退為進、逐步調(diào)整的方法和策略，形成了能進能退的開闊胸襟.這正是一種文化的遷移，一種文化的教育[1].2017年的“數(shù)學文化”試題對中學的教與學起到了基本導向和引領(lǐng)作用.

2.3 高考考查數(shù)學文化的長期性

在數(shù)學高考中加強數(shù)學文化的考查，旨在發(fā)揮高考“指揮棒”的作用，通過考題讓學生感受中國的傳統(tǒng)文化之美并予以傳承.這不是一蹴而就的事情，是一個長期的過程.其實，不僅是2017年的高考，即使在前幾年的全國數(shù)學高考新課標卷和湖北卷等已有了大膽的嘗試，比如：2015年全國數(shù)學高考新課標卷Ⅰ文、理科第6題都考查了《九章算術(shù)》中的“委米依垣”問題、2015年全國數(shù)學高考新課標卷Ⅱ文、理科第8題考查了《九章算術(shù)》中的“更相減損術(shù)”、2016年全國數(shù)學高考新課標卷Ⅱ理科第8題考查了“秦九韶算法”等.

因此，在數(shù)學教與學中，要充分重視對“數(shù)學文化”的學習滲透，特別是要有的放矢地將現(xiàn)行人教版《普通高中課程標準試驗教科書·數(shù)學》中“數(shù)學文化”的典型案例，如必修1中的閱讀材料“中外歷史上的方程求解”；必修2中的探究與發(fā)現(xiàn)材料“祖暅原理與柱體、錐體、球體的體積”；必修3算法案例中的“秦九韶算法、更相減損術(shù)及割圓術(shù)”；必修5中的閱讀材料“海倫和秦九韶”“九連環(huán)”；選修2-3中的探究與發(fā)現(xiàn)材料“‘楊輝三角’中的一些秘密”等學習到位并予以拓展，從而促進學生理性思維的發(fā)展.

[1] 陳昂，任子朝．突出理性思維 弘揚數(shù)學文化[J]．中國考試，2015(3):10-14．

O119

A

1003-6407(2017)10-45-02