對一道向量最值高考試題的三重研究

● (陽新縣高級中學,湖北 陽新 435200)

2017-08-01

鄒生書(1962-)，男，湖北陽新人，中學高級教師.研究方向數學教育.

對一道向量最值高考試題的三重研究

●鄒生書
(陽新縣高級中學,湖北 陽新 435200)

2017年全國數學高考新課標卷Ⅲ理科第12題，是一道以平面幾何圖形為背景、以向量線性表示的等式為呈現方式，求線性系數和最大值的試題.試題在能力立意方面是一道值得深入研究的佳題，文章從一題多解、結論拓展和多題一法這3個方面對這道試題進行了三重研究.

向量;線性表示;最值;高考題;研究

2017年高考已塵埃落定，“研究高考試題，探尋高考新動向，指導高中教學和復習備考”是一線教師面臨的重大課題.全國數學高考新課標卷Ⅲ理科第12題是一道以平面向量為載體求最大值的試題，題目能力立意平中見奇，思路入口寬，解法靈活多樣，既能很好考查考生對基礎知識、基本技能、通性通法的掌握情況，同時考查綜合運用多種數學思想如化歸轉化思想、數形結合思想和函數方程思想分析問題和解決問題的能力，又能有效考查考生運算求解、推理論證和靈活選擇解題策略的能力.下面筆者談談對這道試題從解法到問題推廣，再到這類問題的求解通法的三重研究，希望對讀者有所幫助.

( )

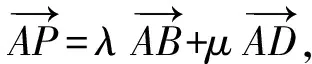
1 解法研究，探求一題多解

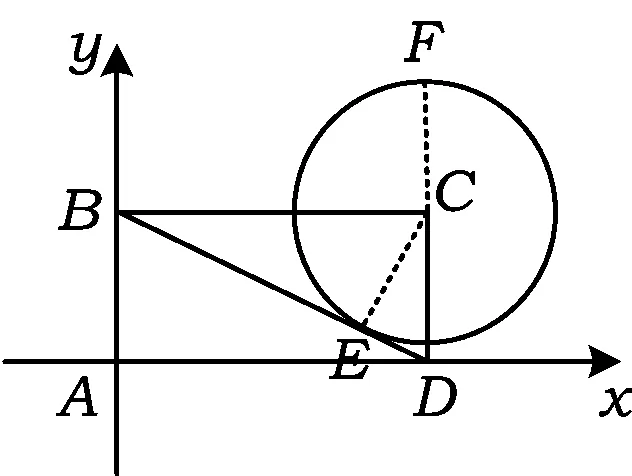
圖1

建立如圖1所示的直角坐標系，設⊙C與BD相切于點E，聯結CE，則CE⊥BD.由面積法得圓的半徑為

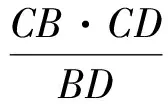
解法1(特殊點法)延長DC交⊙C于點F，則

由題意，得

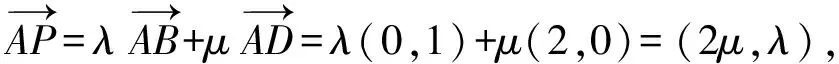
當動點P為點F時,

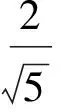
于是

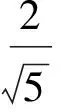
此不等式可用分析法證明.選項B,C,D均不正確，故選A.

解法2(用三角函數求最值)設P(x,y)，則

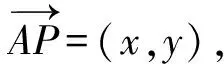
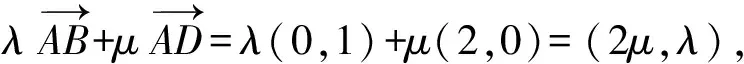
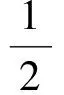
于是

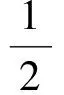
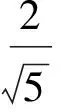
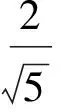
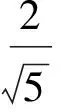
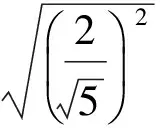
故選A.

解法3(利用直線與圓的位置關系)由解法2得

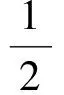
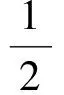
x+2y-2z=0，

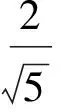
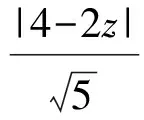
亦即

|z-2|≤1，

解得1≤z≤3.故選A.

解法4(利用線性規劃的思想方法)由解法2得

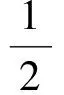
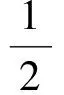
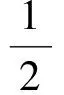
此方程表示經過點P的動直線，其中z就是直線在y軸上的截距.由圖1知:當直線與⊙C相切時,z分別取到最大值和最小值，此時圓心到直線的距離等于半徑，即

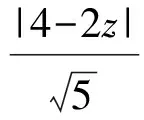
亦即

|z-2|=1，

解得z=1或z=3.其中z=3為最大值.故選A.

點評上述4種解法的共同特點是坐標法，即通過建立直角坐標系將向量問題通過坐標運算轉化為代數問題來處理，即用向量的代數特征求解.下面用向量的幾何特征再給出一種向量解法.

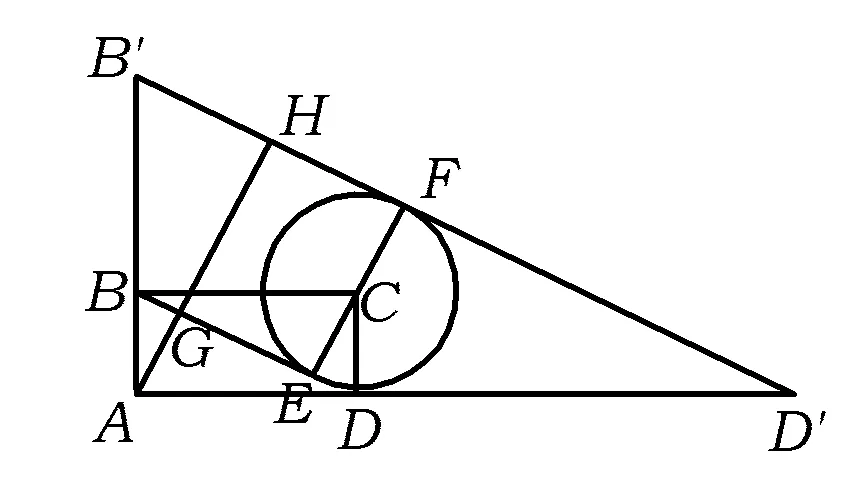
圖2

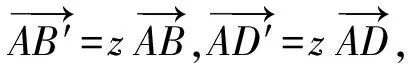
又點P,D′,B′共線，從而

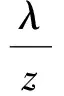
則

z=λ+μ.

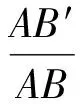
2 縱向研究，探索本質屬性

試題中的矩形較為特殊，λ+μ的最大值和最小值是否與矩形的形狀或大小有關？通過縱向研究發現:λ+μ的最大值和最小值均為定值，與矩形的形狀和大小無關，性質與證明如下:

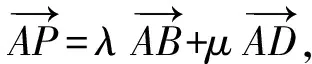
解法1(從圓的參數方程切入，用三角函數求最值)建立如圖1所示的直角坐標系，設⊙C與BD相切于點E，聯結CE，則CE⊥BD.由面積法得圓的半徑為

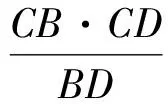
設點P(x,y)，則

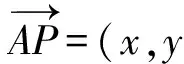
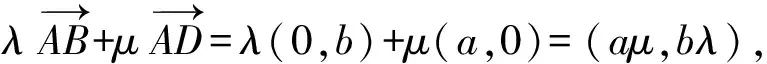
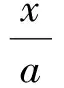
則

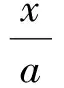
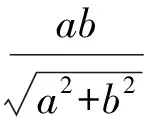
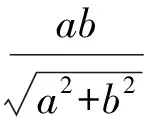
所以

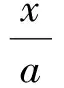
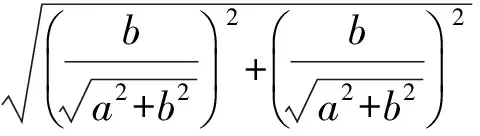
故λ+μ的取值范圍是[1,3].

bx+ay-abz=0，

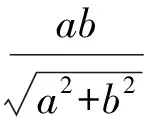
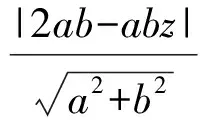
亦即

|z-2|≤1，

解得

1≤z≤3,

故λ+μ的取值范圍是[1,3].

解法3(利用線性規劃的思想方法)由例1的解法2可得

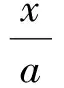
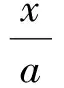
此方程表示經過點P的動直線，其中bz就是直線在y軸上的截距.由圖1知:當直線與圓相切時,bz分別取到最大值和最小值，從而z分別取到最大值和最小值.此時圓心到直線的距離等于半徑，即

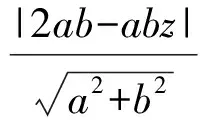
化簡得

|z-2|=1，

解得z=1或z=3.故λ+μ的取值范圍是[1,3].

解法4(向量方法)與例1的解法5類似，這里從略.

3 橫向研究，探尋通性通法

將這道高考題的幾何背景一般化，可得如下一般性問題：

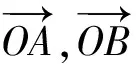
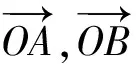
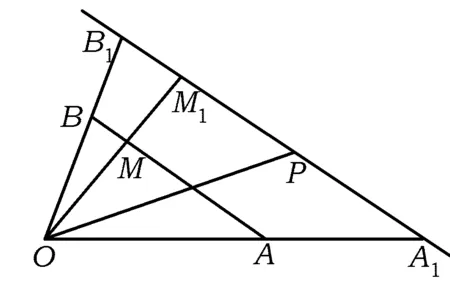
圖3

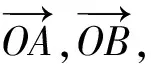
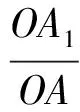
當直線l與AB在點O的兩側時，

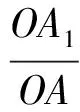
證明因為AB∥A1B1，所以

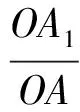
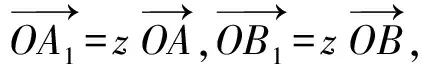
又因為點P,A1,B1共線，所以

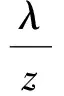
則

λ+μ=z.

當直線l與AB在點O的同側時，z>0，則

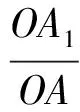
當直線l與AB在點O的兩側時，z<0，則

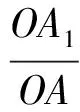
下面舉例說明直接運用等高線定理可簡單快捷地解答這類問題.

例3在ABCD中，E,F分別為CD,BC的中點，若其中λ,μ∈R，則λ+μ=______.

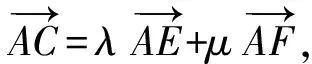
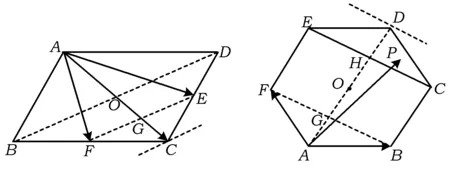
圖4 圖5

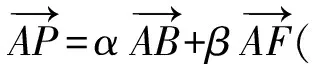
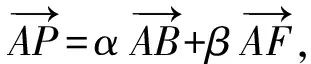
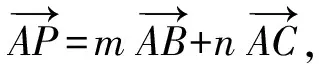
(2011年江西省南昌市數學聯考試題)

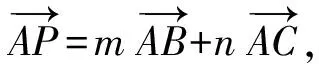
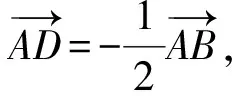
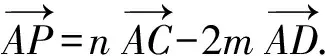
過點P作CD的平行線l，由定理1知:當點P與點C重合時，

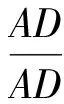
當點P與點B重合時,

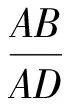
又因為P是△ABC內任一點，所以n-2m的取值范圍是(-2,1).

點評本解法需要根據所求最值式n-2m構造新基底，靈活運用定理1,從而使問題獲解.

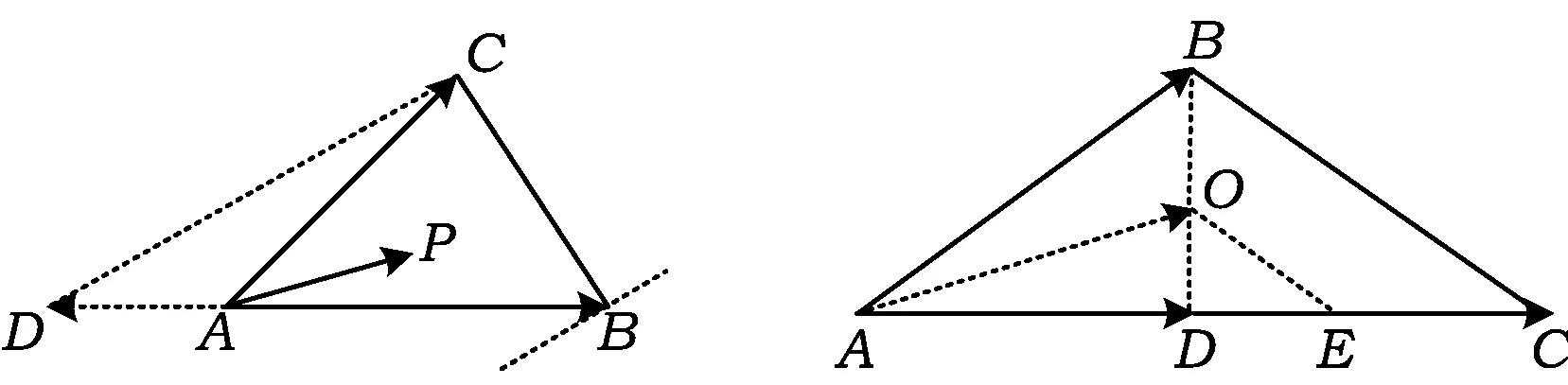
圖6 圖7

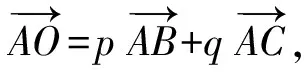
(2012年全國高中數學競賽湖北省預賽高一試題第7題)

解如圖7，聯結OA,OB，因為O是△ABC的內心，所以OA,OB分別平分∠BAD和∠ABC.延長BO交AC于點D，因為AB=BC=2，所以點D是線段AC的中點.作OE∥BC交AC于點E，因為AO是△ABD的內角平分線，由三角形內角平分線性質定理得

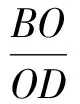
由OE∥BC，得

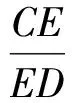
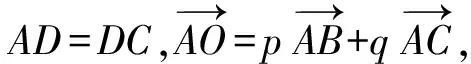
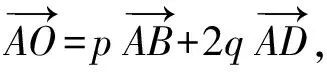
又點B,O,D共線，所以

由式(1)和式(2)，得

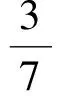
故

( )

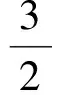
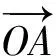
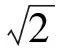
(2013年安徽省數學高考理科試題第9題)

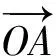
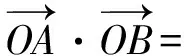
從而

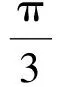
圖8

S= 4S△OAB=

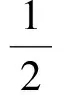
故選D.

評注上述向量解法本質上與二元線性規劃問題中求線性目標函數的最值或取值范圍的圖解法完全類似,用的都是平行線法，如果最值存在，其值都在可行域的邊界上取得.用平行等高線法求這類問題的值域，對學生來說確實理論要求較高，但起點高落點低，解法形象直觀，一旦掌握則答案唾手可得.

筆者對例1進行了3個維度的研究：1)試題解法研究，即一題多解，多角度、多方位用多種數學知識和思想方法解決試題，在高三復習備考時可達到以點帶面、做一題復習一大片的效果；2)對試題縱向研究，即將題目的部分條件一般化研究一般性問題的一般性結論，有利于看清問題的本質屬性，對問題有比較深刻的理解；3)橫向研究，即將問題放到一個更加普遍的一類問題上進行研究，主要研究這類問題的通性通法，達到多題一法、一法解一類題之目的.

[1] 鄒生書.構建仿射坐標系解題[J].河北理科教學研究，2012(2)：36-39.

[2] 康井榮，蘇良國.向量等式轉化的幾種策略[J].中學數學雜志，2017(5)：44-46.

[3] 鄒生書.2013年高考平面向量精彩試題賞析[J].數理化學習,2013(10)：2-3.

O123.1

A

1003-6407(2017)10-33-05