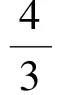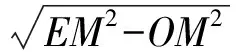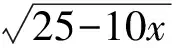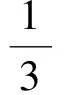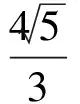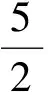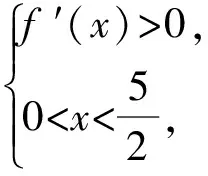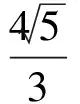對2017年全國卷Ⅰ理科第16題的尋源探變

● (虞陽中學,福建 福清 350307)

2017-07-28

教育部福建師范大學基礎教育研究中心2017年開放課題(KC-2017053)

湯小梅(1971-)，女，福建福清人，中學高級教師.研究方向數學教育.

對2017年全國卷Ⅰ理科第16題的尋源探變

●湯小梅
(虞陽中學,福建 福清 350307)

高中數學應用一題多解與一題多變的方法，讓學生將所學知識進行靈活運用，并開拓思路，從而做到融會貫通．這就需要我們面對數學試題，學會多角度欣賞與思考，從中發現試題的解決規律，并能尋“根”探“源”與同“源”探“變”，進而掌握一類題的應對策略．

一題多解;尋根探源;同源變式

1 試題展現

例1如圖1，圓形紙片的圓心為O，半徑為5 cm，該紙片上的等邊△ABC的中心為O．D,E,F為⊙O上的點，△DBC，△ECA，△FAB分別是以BC，CA，AB為底邊的等腰三角形．沿虛線剪開后，分別以BC，CA，AB為折痕折起△DBC，△ECA，△FAB，使得點D,E,F重合，得到三棱錐．當△ABC的邊長變化時，所得三棱錐體積(單位：cm3)的最大值為______．

(2017年全國數學高考卷Ⅰ理科試題第16題)

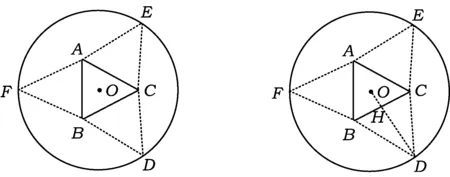
圖1 圖2

點評這道高考題文字表述流暢、圖像優美，令人賞心悅目．借用平面圖形的翻折為背景，考查利用導數解決三棱錐體積的最大值問題，意在考查學生的空間想象能力、轉化和化歸能力、實際應用能力以及運算求解能力．在近5年的新課標試卷中，利用導數解決最優化問題是首次考查，此類考題規避了特殊技巧，凸現了數學本質，能有效地考查學生的創新意識，培養學生的應用意識．

2 解法探究

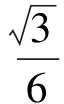
從而三棱錐的高為

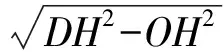
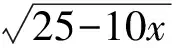
于是

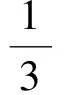
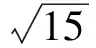
f′(x)=20x3-10x4.

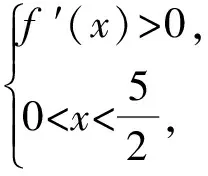
f(x)max=f(2)=16，

于是

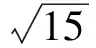
解法2聯結OD,交BC于點H(如圖2),設AB=2x，則

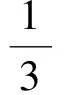
從而三棱錐的高為

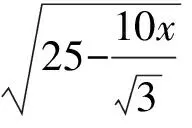
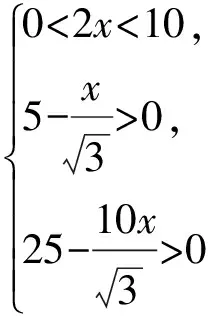
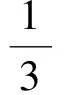
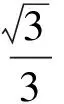
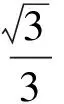
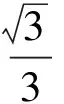
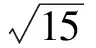
點評在上述的兩種解法中，解法1是常規解法，為大多數學生所選．通過觀察已知圖形特征，設弦心距為x，快速找到三棱錐的體積是關于x的函數，借用“導數”的工具性，通過求導，判斷函數的單調性，求出三棱錐體積的最大值．注意隱蔽條件“自變量在實際意義中的取值范圍”在解題中的應用．解法2設正三角形的邊長為2x，求出三棱錐的體積關于x的函數，借用“5個正數的算術—幾何平均不等式”(也稱基本不等式的推論)，展現了基本不等式的推論在求最值中的威力和魅力，充分顯示了解法的靈活性，實屬巧思妙解，干凈利落，意猶未盡．

3 尋根探源

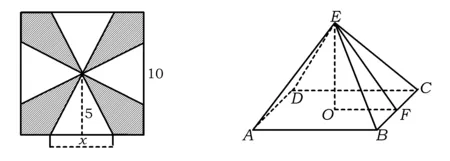
圖3 圖4

例2[1]一塊邊長為10 cm的正方形鐵片按如圖3所示的陰影部分裁下，然后用余下的4個全等的等腰三角形加工成一個正四棱錐(底面是正方形，從頂點向底面作垂線，垂足是底面四棱錐的中心)形容器(如圖4)，試把容器的容積V表示為x的函數．

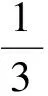
(人教A版《數學(必修2)》第37頁復習參考題B組第4題)

例3[2]用半徑為R的圓形鐵片剪出一個圓心角為α的扇形，制成一個圓錐形的容器，問：扇形的圓心角α多大時，容器的容積最大？

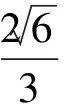
(人教A版《數學(選修2-2)》第67頁復習參考題B組第3題)

例1是例2和例3的整合：只需把“圓形鐵皮或正方形鐵片”變為“圓形紙片”，把“圍成圓錐或四棱錐”變為“三棱錐”，并把結論“容器的容積最大時的自變量的值或容積V表示為x的函數”變為“求三棱錐體積的最大值”，即得例1．在強調命題改革的今天，通過改編、創新等手段來賦予課本例題、習題新的生命，這已成為高考命題的一種新走向．近幾年高考試題的命制越來越新穎多變，尤其是對不等式的考查，形式多樣，但萬變不離其宗，大多數高考題都能在課本中找到其原型.因此，我們在高三復習備考的過程中要注意對課本例題、練習題的訓練，把握其實質，掌握其規律，規范其步驟，做到“胸中有本”.

4 同源變式

俗話說：“鐵打的營盤，流水的兵．”高考中不變的是知識，變化的是情景的呈現形式、問題的結構方式．這就要求我們面對數學題能突破常規，陳題巧改編，舊瓶裝新酒．

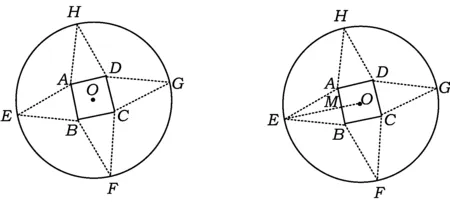
思考1把例1的背景精雕細琢，變為實際生活中的應用問題，并把“圓形紙片的半徑為5 cm”變為“圓形包裝紙的半徑為10 cm”，便可得到如下立意新穎、構思獨特的好題[3]：

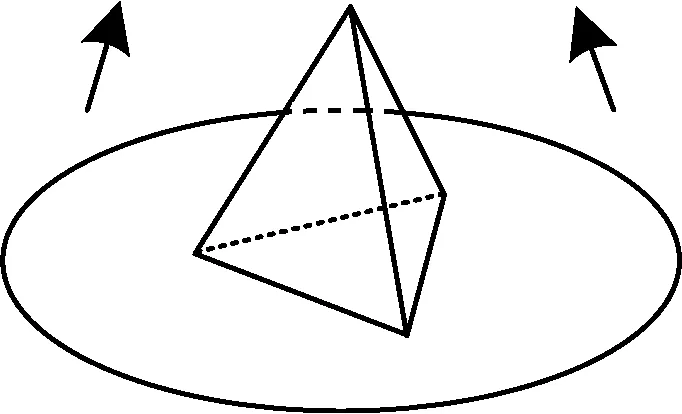
圖5

變式1某商場為促銷要準備一些正三棱錐形狀的裝飾品，用半徑為10 cm的圓形包裝紙包裝．要求如下：正三棱錐的底面中心與包裝紙的圓心重合，包裝紙不能裁剪，沿底邊向上翻折，其邊緣恰好達到三棱錐的頂點(如圖5)．設正三棱錐的底面邊長為xcm，體積為Vcm3，在所有能用這種包裝紙包裝的正三棱錐裝飾品中，V的最大值是______，此時x的值為______．

思考2去掉高考題中的圖形的翻折背景，并把條件中的“正三棱錐”變為直接呈現“正四棱錐”，并添加條件“側棱長為1”，結論還是“求體積的最大值”，即可得到如下題意簡潔、清晰的好題：

變式2設正四棱錐的側棱長為1，則其體積的最大值為______．

分析設正四棱錐的底面邊長為x，則體積為

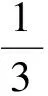
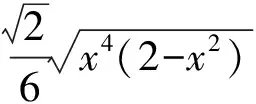
設x2=t(其中0

y=t2(2-t)=2t2-t3，

從而

y′=4t-3t2=-t(3t-4)，

思考3仍用例1的背景，只是把條件與結論中的“三棱錐”變為“四棱錐”，即可得如下“新口味”的好題：

變式3如圖6，圓形紙片的圓心為O，半徑為5 cm，該紙片上的正方形ABCD的中心為O．E,F,G,H為⊙O上的點，△EAB,△FBC,△GCD,△HDA分別是以AB,BC,CD,DA為底邊的等腰三角形．沿虛線剪開后，分別以AB,BC,CD,DA為折痕折起△EAB,△FBC,△GCD,△HDA，使得點E,F,G,H重合，得到四棱錐．當正方形ABCD的邊長變化時，所得四棱錐體積(單位：cm3)的最大值為______．

圖6 圖7

分析聯結OE，交AB于點M(如圖7)，則OE⊥AB.設OM=x，則BC=2x，EM=5-x,從而四棱錐的高為

且

S正方形ABCD=4x2,

f′(x)=20x3-10x4.

f(x)max=f(2)=16，

于是

由上可知:課本素材是高考考題編擬的藍本，對高考典型試題進行多角度思考，實際上是對高考試題的“二次開發”，即通過一道題，明晰一類題．對典型試題，尤其是涉及核心知識內容的典型試題的剖析和思考更是必不可少，通過對典型試題的靈活變換和多角度思考，展開問題的來龍去脈和知識間的縱橫聯系，讓學生站在一定的高度去思考問題，突出數學的本質，使學生的思維得到提升，使知識達到融會貫通.如此，不論高考題的構思多么新穎，學生也能做到以不變應萬變．

[1] 課程教材研究所.普通高中課程標準實驗教科書·數學(必修2)[M].北京：人民教育出版社，2016：37.

[2] 課程教材研究所.普通高中課程標準實驗教科書·數學(選修2-2)[M].北京：人民教育出版社，2014：67-67.

[3] 編寫組.2017高考數學經典題型與變式[M].北京：西藏人民出版社，2016.

O123

A

1003-6407(2017)10-38-03