觸及題目的背后
——談高三數列復習

● (常州市第一中學,江蘇 常州 213003)

2017-08-30

江蘇省教育科學“十二五”規劃課題(B-a/2015/02/008)

陸建明(1981-)，男，江蘇溧陽人，中學一級教師.研究方向數學教育.

觸及題目的背后
——談高三數列復習

●陸建明
(常州市第一中學,江蘇 常州 213003)

文章從2017年江蘇省南通市二模數學卷第20題引入，探索此題的背景，指出評講高三數列壓軸題應該兼顧一輪、推而廣之、旁征博引，從而真正實現高三復習定位于突出重點、掌握思想、學會探究的目標，即提升能力,力爭突破難題.

等差數列;等比數列;好數列

高三下學期復習,在學生系統掌握了基礎知識和基礎方法后，教學更多的是以練帶動復習，此時教師評講作業如果和學生一樣只是就題論題，那么學生怎會有質的飛躍，怎會有深刻認識，并形成深刻的反思！作為教師，要給學生一碗水，自己必需有一桶水，站在更高的高度看待高三復習，復習目標應該定位于突出重點、掌握思想、學會探究，即提升能力,力爭突破難題.下面以2017年江蘇省南通市二模數學卷第20題評講為例，站在更高的高度探索數列終極復習.

例1設數列{an}的前n項和為Sn(其中n∈N*)，且滿足：

① |a1|≠|a2|;

②r(n-p)Sn+1=(n2+n)an+(n2-n-2)a1,其中r,p∈R,且r≠0.

1)求p的值；

2)數列{an}能否是等比數列？請說明理由；

3)求證：當r=2時，數列{an}是等差數列.

分析1)p=1；2)利用特值法得到{an}不是等比數列,過程略.

3)證明由題意可得

2(n-1)Sn+1=(n2+n)an+(n2-n-2)a1.

當n=1時，上式恒成立.

當n≥2時，

上式賦n為n+1，得

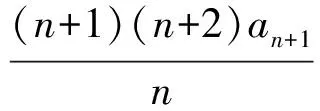
(2)

式(2)-式(1)，得

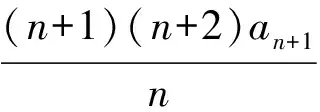
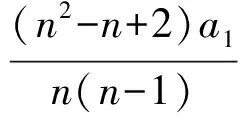
兩邊同除n+1,得

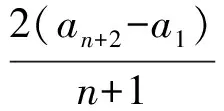
令bn=an-a1,得

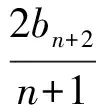
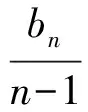
2cn+2=(n+2)cn+1-ncn

即

2(cn+2-cn+1)=n(cn+1-cn).

令dn=cn+1-cn,得

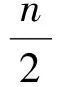
累乘可得

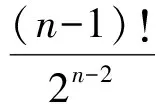
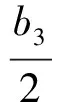
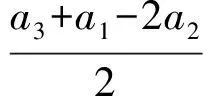
從而

dn=0.

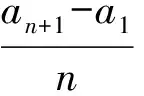
an=a1+(n-1)(a2-a1).

經檢驗，n=1符合上式.

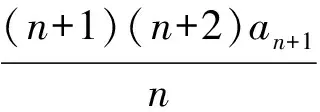
教師引領，站在一定的高度反思這個問題：條件r(n-1)Sn+1=(n2+n)an+(n2-n-2)a1是整個題目的核心，r=2怎么來的呢？事實上，反過來想：如果數列{an}是等差數列，那么可以借助基本量化簡得

r(n-1)Sn+1=

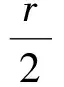
(3)

(n2+n)an+(n2-n-2)a1=

n(n+1)a1+(n-1)n(n+1)d+(n-2)(n+1)a1=

2(n-1)(n+1)a1+n(n+1)(n-1)d,

(4)

對比可以發現，當r=2時，式(3)和式(4)相等，因此可以大膽猜測當r=2時，數列{an}是等差數列.此外，還有其他角度的解釋嗎？

如果只是滿足于解決這一道題目，那么學生不可能發現其背后的問題，更沒法做到深度地思考與反思.正好在前面的復習中，我們遇到了一個“好數列”的題目.

例2設數列{an}的前n項和為Sn，我們稱滿足條件：“對任意的m，n∈N*,均有(n-m)Sn+m=(n+m)(Sn-Sm)”的數列{an}為好數列(問題略).

對于這個問題，我們需要思考的是:上述定義的來源是什么，滿足“好數列”的背景是什么？事實上，經過嘗試，我們發現等差數列滿足上述定義，也就是如果{an}是等差數列，那么可以證得

(n-m)Sn+m=(n+m)(Sn-Sm).

反思第一輪中做過的一道題目：

例3已知數列{an}是等差數列，其前n項和為Sn，且Sn=m,Sm=n(其中m,n∈N*,m≠n)，則Sm+n=-(m+n).

事實上，這是一個很實用的等差數列性質，在文獻[1]中有詳細解析.由此可以猜想數列中有很多問題都是可以反過來思考的，這與文獻[2]的研究思路類似.如：

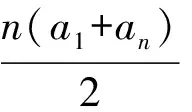
2)若數列{an}的前n項和為Sn，且對任意的m,n∈N*，都有

(n-m)Sn+m=(n+m)(Sn-Sm),

則{an}是等差數列；

3)若{an}的前n項和為Sn=A-Aqn(其中A是不為0的常數，q≠0且q≠1),則{an}是等比數列；

4)若數列{an}的前n項和為Sn，且對任意m,n∈N*,都有

Sm+n=Sn+qnSm(其中q≠0)，

則{an}是等比數列.

上述含有參數m,n的數列性質，有點類似抽象函數表達式的來源.回到例1，將已知條件作進一步思考：

2(n-1)Sn+1=(n2+n)an+(n2-n-2)a1，

取其中1為任意的正整數m，上式可以變形為

2(n-m)Sm+n= [n2+n-(m2-m)]an+

[n2-n-(m2+m)]am，

我們大膽利用上述思想推而廣之.

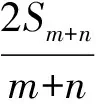
思路1取m=1，回到例1中的證明.

思路2賦m=2,n=1,得

a1+a3=2a2；

賦m為n+1，得

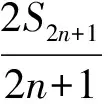
即S2n+1=(2n+1)an+1；

(5)

再賦m為n+2,n為n-1，得

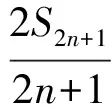
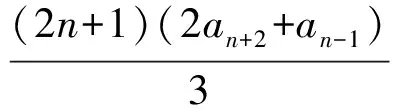
(6)

由式(5)和式(6)可得

3an+1=2an+2+an-1，

從而 2(an+2-an+1)=an+1-an+an-an-1.

令bn=an+1-an,得

2bn+1=bn+bn-1,

即

2(bn+1-bn)=-(bn-bn-1).

又因為b2-b1=a3+a1-2a2=0，所以

bn-bn-1=0，

即

an+1-an=an-an-1，

故數列{an}是等差數列.

評注上述問題給學生提供了更大的思維空間，并且將問題推廣到更一般的情況，讓學生從一定的高度進行思考與分析，為日后遇到類似問題提供方法.

例5已知數列{an}的各項均為正數，其前n項和為Sn，且對任意的m,n∈N*,(Sm+n+S1)2=4a2ma2n.

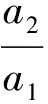
2)求證：{an}為等比數列.

1)解令m=n=1，可得

因為a1>0,a2>0，所以

a2+2a1=2a2，

即

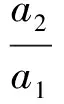
2)證明令m=1,n=2,得

(2a1+a2+a3)2=4a2a4.

令m=n=2,得

S4+S1=2a4,

即

2a1+a2+a3=a4,

從而

a4=4a2=8a1，

于是

a3=4a1.

又(Sn+1+S1)2=4a2na2,(Sn+2+S1)2=4a2na4,兩式相除可得

即

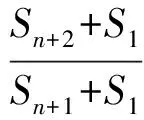
亦即

Sn+2+S1=2(Sn+1+S1)，

進而

Sn+3+S1=2(Sn+2+S1)，

上面兩式相減可得an+3=2an+2.經檢驗：當n≥2時，均有an=2an-1，故數列{an}為等比數列.

數學本身是一個整體，教師只有站在學科的高度看問題，深入挖掘知識點之間的聯系，深刻領會數學思想的教育價值，才能充分抓住機會，引導學生從整體、系統的角度進行分析,積極探索數學問題的“本源”，從而積累數學活動的經驗，提升數學分析問題、解決問題的能力，提高數學的核心素養.

[2] 陸建根.一道試題的深度研究[J].中學數學教學參考，2016(7):39-41.

O122.1

A

1003-6407(2017)10-20-03