基于基本圖形的自然解法

● (鄞州實驗中學，浙江 寧波 315100)

2017-06-19

蔡衛兵(1976-)，男，浙江象山人，中學高級教師.研究方向數學教育.

基于基本圖形的自然解法

●蔡衛兵
(鄞州實驗中學，浙江 寧波 315100)

文章從基本圖形出發，嘗試通過添加輔助線來解答初中幾何問題，從而找到解題的切入口，順利地把條件與結論有機串聯起來，使得解法簡潔、流暢.基本圖形是輔助線添加的源頭，它驅動著思維起航，催生著解題思路的自然、連貫.

數學解題；基本圖形；自然解法

1 題目再現

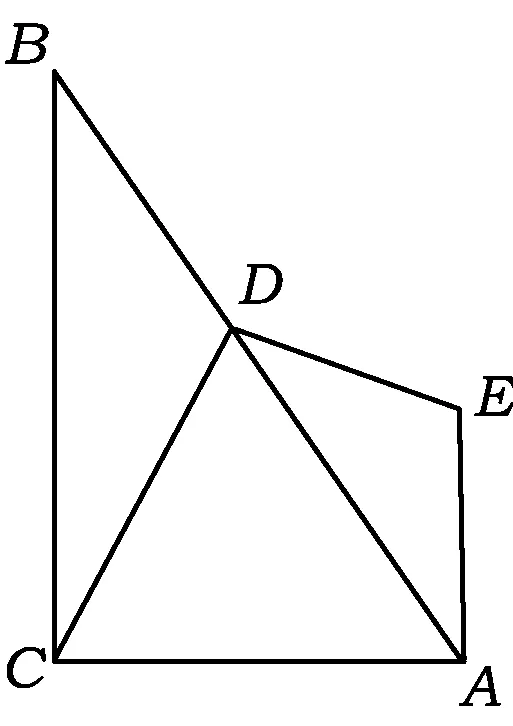
圖1

題目如圖1，在△ABC中，∠ACB=90°，∠CBA=30°，D是AB上任意一點，聯結DC，作DE⊥DC，EA⊥AC，DE與AE交于點E，則DE,DC有什么數量關系？請給出證明.

本文基于6種基本圖形(如圖2所示)，用13種解法解決了該問題.

① ② ③

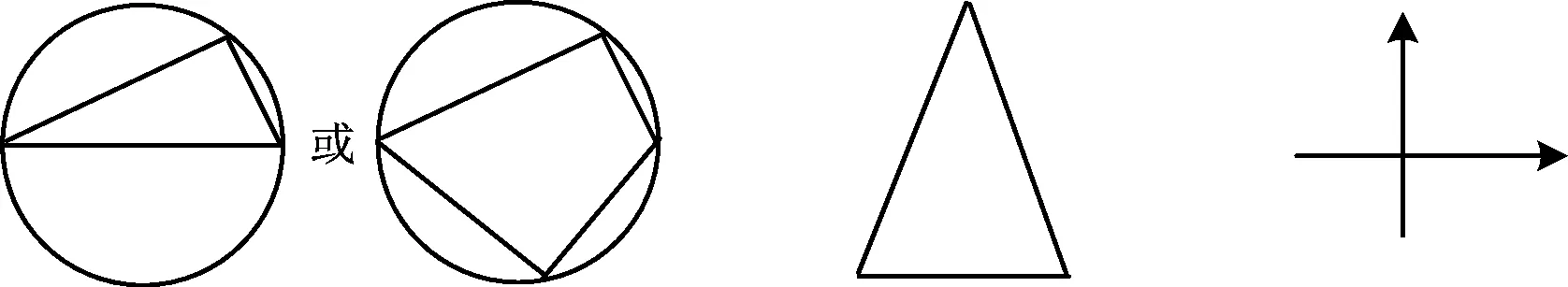
④⑤⑥

2 解法展示與思考

2.1 基本圖形①

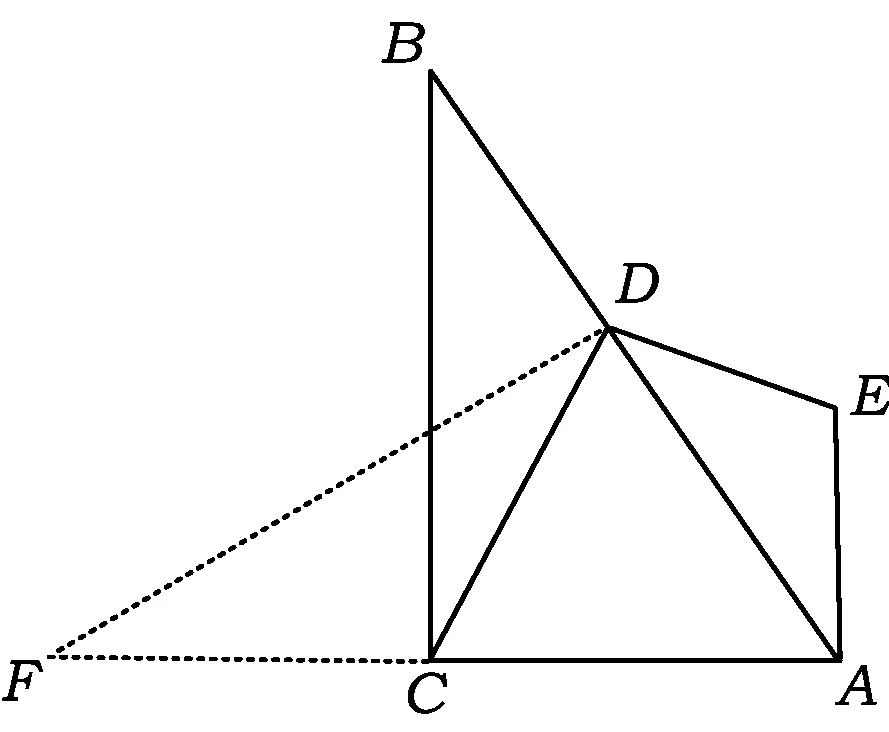
圖3

解法1如圖3，過點D作DF⊥AB,且DF與AC的延長線交于點F.因為DE⊥DC，所以

∠FDC=∠ADE.

又EA⊥AC，從而

∠F=∠DAE,

于是△FDC∽△ADE,進而

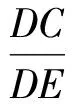
由∠ACB=90°，∠CBA=30°，知

∠FAD=60°.

因此在Rt△FDA中,

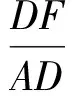
故

解法2如圖4，過點D作DF⊥AB，且DF與AE的延長線交于點F.由解法1得

△ADC∽△FDE，

從而

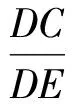
又由解法1得∠F=60°，于是

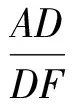
故

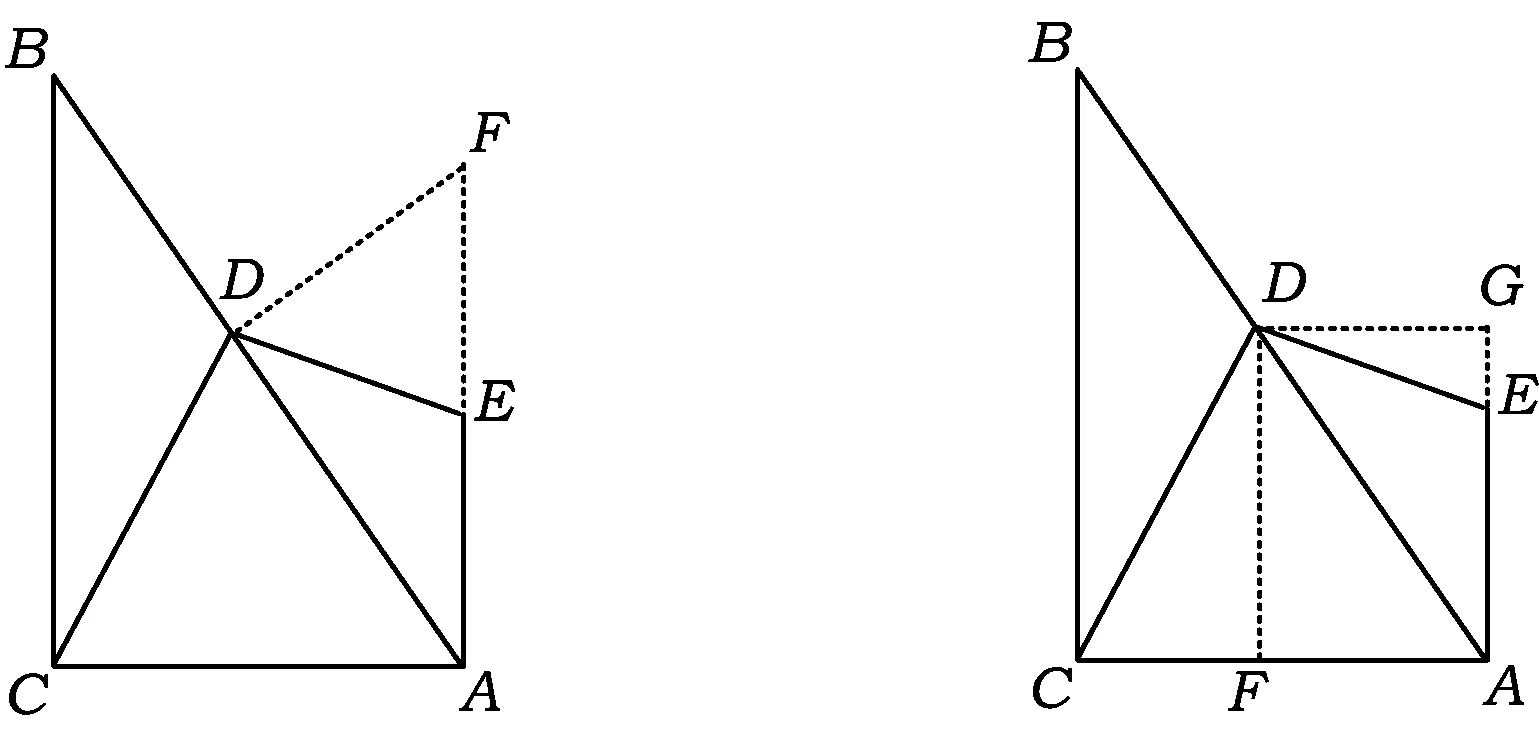
圖4 圖5

解法3如圖5，過點D作DF⊥AC，DG⊥AE，垂足分別為F，G.由EA⊥AC可知四邊形AGDF為矩形，從而DG=FA.同解法1得∠FAD=60°，于是

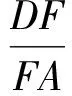
又∠CDF=∠EDG，從而

Rt△CDF∽Rt△EDG，

于是

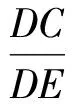
故

思考關于有公共頂點的雙直角的基本圖形模型，這是浙教版《數學》七年級上冊“余角和補角”中的例題:指出圖中哪些角是互余的？哪些角是相等的？顯然根據同角的余角相等已證一對銳角相等，接著考慮將要求的兩條線段DC,DE分別放到已得的一對角相等的兩個三角形中，然后只需再證一對角相等便可判定兩個三角形相似，借助相似三角形的對應邊成比例將要求的“線段DC,DE之比”轉化為“已知關系的兩線段之比”.由于學生對此種基本圖形模型比較熟悉，相似三角形的構造、判定、性質運用比較常見，因此解法1～3的輔助線容易想到，求解過程比較常規，是學生自然而然能想到的方法.

2.2 基本圖形②

解法4如圖6，過點D作GF⊥BC，且GF與BC交于點G，與AE的延長線交于點F.由∠ACB=90°，EA⊥AC可知四邊形ACGF為矩形，從而CG=FA.易證∠DCG=∠FDE，于是

Rt△CDG∽Rt△EDF，

因此

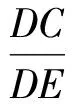
易得

∠FDA=60°，

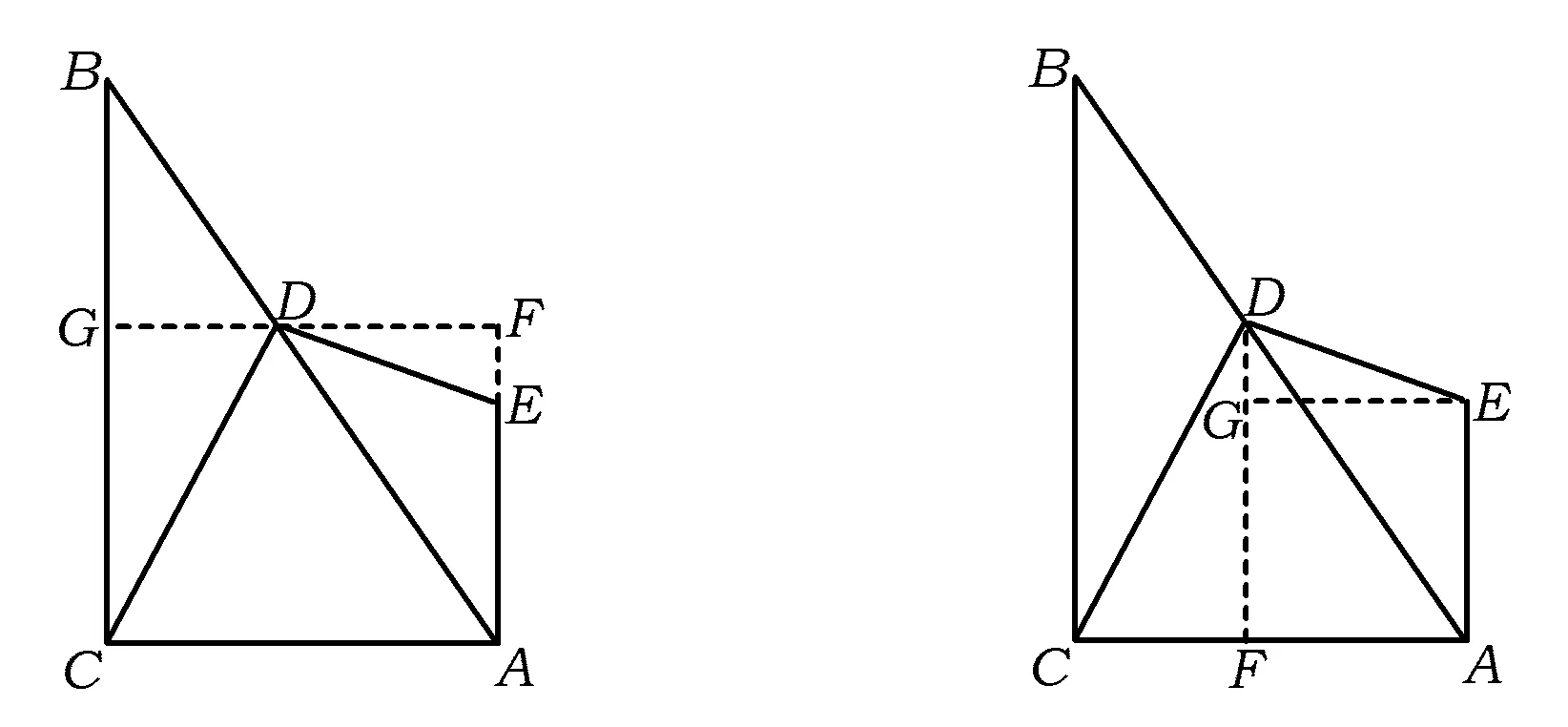
圖6 圖7

解法5如圖7，過點D作DF⊥AC，垂足為F，過點E作EG⊥DF，垂足為G.同解法4可知四邊形AFGE為矩形，從而EG=FA,同解法4又可得

Rt△CDF∽Rt△DEG，

于是

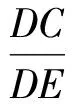
因為

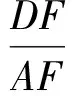
所以

圖8

解法6如圖8，過點C作CF⊥AB，垂足為F，過點E作EG⊥AB，垂足為G.同解法5可得

Rt△CDF∽Rt△DEG，

從而

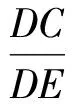
于是

CF·EG=DG·DF.

由Rt△ACF∽Rt△EAG,得

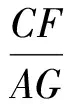
從而

CF·EG=AG·AF,

于是

DG·DF=AG·AF，

即

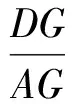
因此

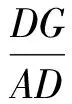
進而

DG=AF,

于是

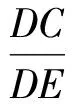
故

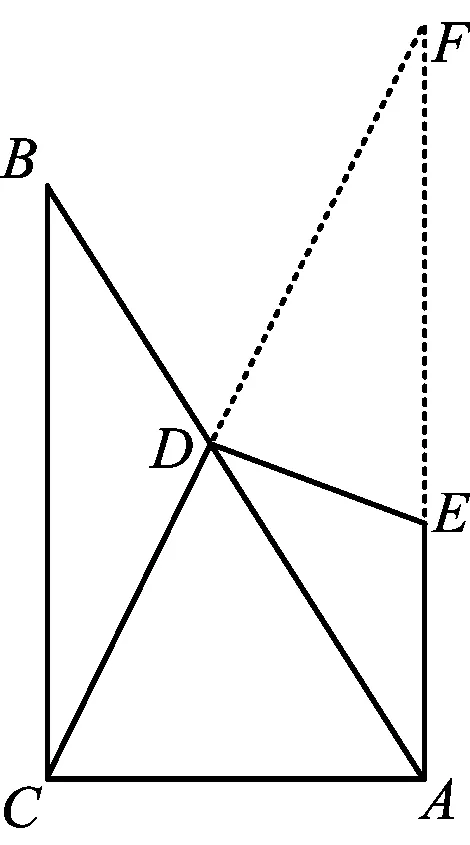
圖9

思考關于3條邊分別互相垂直的兩個直角三角形的基本圖形模型，這是浙教版《數學》八年級上冊“全等三角形”和九年級上冊“相似三角形”中的作業題，提煉模型：如果兩個直角三角形對應邊互相垂直，當對應邊相等時，那么這兩個直角三角形全等；當對應邊不相等時，那么這兩個直角三角形相似[1].解法4～6的本質相同，都是通過作輔助線構造“三垂直”相似模型，前兩種線段之間的代換不涉及任何技巧，這也是比較接近學生的最近發展區的一種解題思路.其中解法6需要比例式與等積式之間的多次轉化，運用合分比性質得出DG=AF使問題得解，其所蘊涵的思維量和所涉及的計算能力不是學生能自然而然所獲得的.

2.3 基本圖形③

解法7如圖9，延長CD交AE的延長線于點F.由∠ACB=90°和EA⊥AC得BC∥AF，從而△BCD∽△AFD，于是

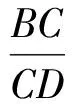
由∠F=∠F，∠FDE=∠FAC=90°得

△FAC∽△FDE，

從而

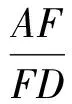
于是

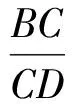
因此

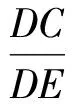
故

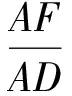
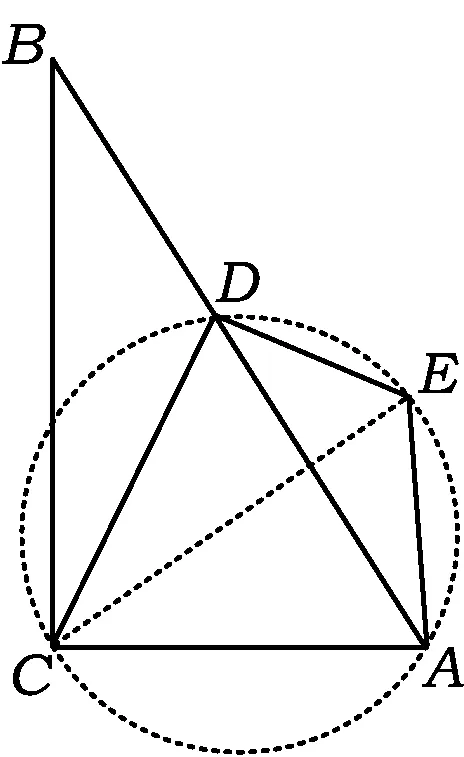
圖10

2.4 基本圖形④

解法8如圖10，聯結CE，作△CDE的外接圓，因為DE⊥DC，所以CE為圓的直徑，又EA⊥AC，從而點A在以CE為直徑的圓上，即點A,C,D,E在同一個圓上.由圓周角定理推論知

∠DEC=∠DAC=60°，

從而

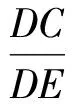
于是

思考“直徑所對的圓周角是直角；90°的圓周角所對的弦是直徑；圓的內接四邊形的對角互補”是圓的基本性質，學生能比較熟練地想到運用上述性質，通過補上輔助的隱形圓，是此種解法的突破口，接著利用“同弧所對的圓周角相等”和銳角三角函數就能順利求解.

2.5 基本圖形⑤

解法9如圖11，截取DF=DC，作∠GDA=∠EAD=30°.在四邊形ACDE中,

∠CDE=∠CAE=90°，

從而

∠DCA+∠E=180°.

因為∠DFC+∠DFA=180°，∠DCF=∠DFC，所以

∠DFA=∠E.

又因為∠DAF=60°，∠DGE=∠GDA+∠EAD=60°，所以

∠DAF=∠DGE,

從而

△DAF∽△DGE，

于是

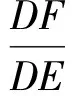
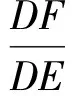
即

故

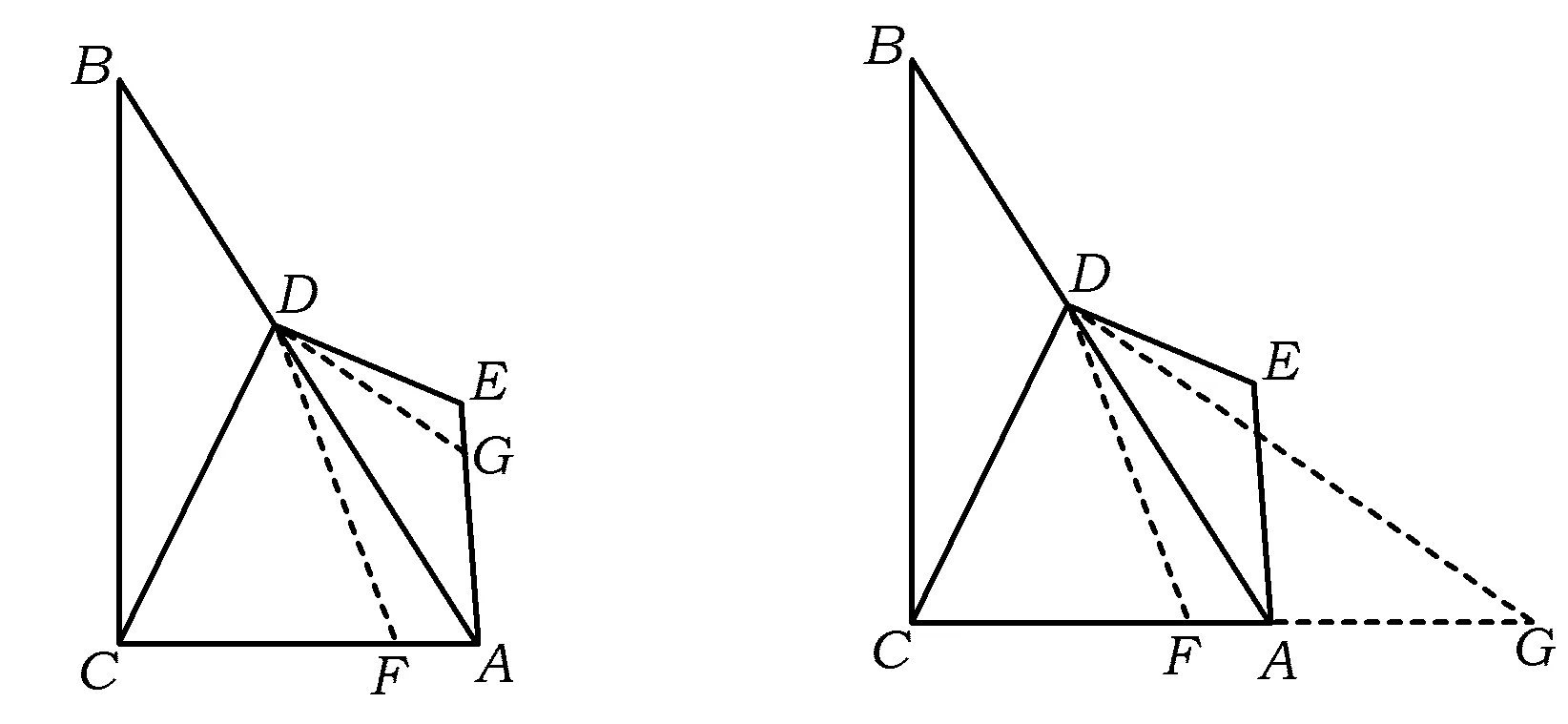
圖11 圖12

解法10如圖12，截取DF=DC，AG=AD，聯結DG.同解法9得

∠DFA=∠E,

因為∠DAF=∠G+∠ADG=60°，∠G=∠ADG，所以

∠G=30°.

又∠DAE=30°，從而

∠G=∠DAE,

于是

△DFG∽△DEA，

因此

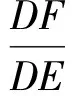
于是

故

解法11如圖13，截取DF=DE，作∠GDA=∠EAD.同解法9得

∠F=∠DCA， ∠DGF=∠DAC=60°,

從而

△DAC∽△DGF，

于是

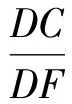
因此

故

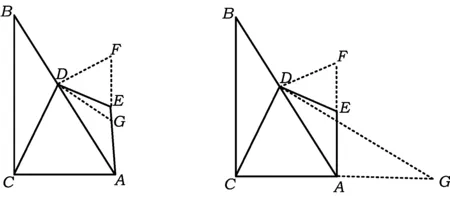
圖13 圖14

解法12如圖14，截取DF=DE，AD=AG，聯結DG.同解法10得

∠F=∠DCA， ∠DAF=∠G=30°,

從而

△DCG∽△DFA，

于是

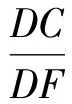
因此

故

思考以上4種解法本質相同，都是基于“等腰三角形的兩腰相等進行線段之間的轉化”和“等腰三角形的兩底角相等進行角之間的轉化”，接著依賴于視點的依次轉換，順勢而思，通過構造包含相關的線段和已有的相等角的相似三角形：解法9和解法11再構造一對60°的角，解法10和解法12再構造一對30°的角，然后借助頂角為120°的等腰三角形的腰和底邊之間的關系加以求解.這里解題思路的探尋一環扣一環，完全根據解題的需要，步步推進，但整個構造轉化的過程較為復雜，學生獲得這4種解法有一定的難度.

2.6 基本圖形⑥

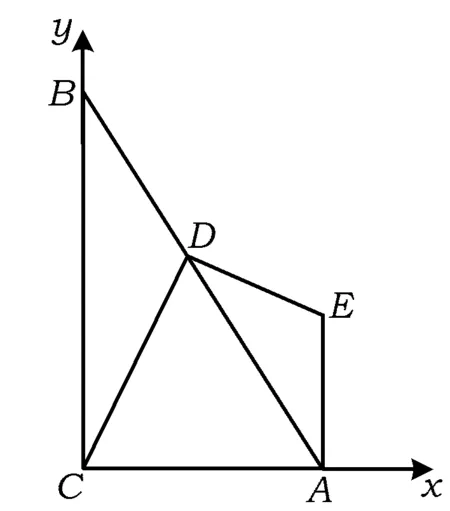
圖15

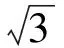
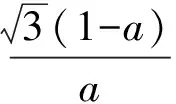
直線DE的解析式為

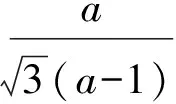
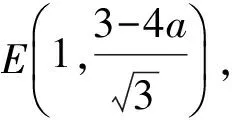
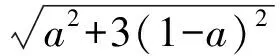
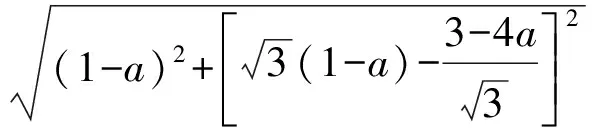
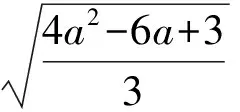
故

思考“定位”是坐標系特有的本領，根據本題的條件易將這個圖形放在一個合適的平面直角坐標系中來思考，逐一定點、定線、定距離，通過“以數解形”使問題的解決水到渠成.用字母表示圖中有關點的坐標或直線解析式或線段的長度，體現出符號意識，計算較繁瑣，這是學生很難實現的“自然解法”.

3 反思

崇尚自然、重視常規而淡化技巧性是數學解題教學的一個方向和追求.方法的生成應該從學生已有的知識經驗和思考基礎出發，從記憶儲存中提取有關的基本圖形和常用結論,選擇準確、科學的思維起點，使得解題的思路更加開闊，輔助線的添加也更為自然，從而催發方法自然生長[2].從思維的角度看，基于基本圖形的數學模型解題體現思維定勢正遷移的積極作用，化生為熟，化非常規為標準題的化歸過程；從方法論的角度看，借助基本圖形的數學模型思考問題，既可防止無關信息的負面干擾，又能以“塊到塊”的思維模式代替“點到點”的思維模式，提高思維的敏捷性.

在平時的解題教學過程中，教師要善于引導學生將所學的內容整理歸納出類型和方法，經過加工提煉，得出有長久保存價值的基本圖形的數學模型，有意識地記憶下來，在新問題中喚醒頭腦中積累的基本圖形，并選擇較簡單的求解過程的數學模型加以運用，從而建構解決問題的方法體系.這樣，學生頭腦中能快速辨認、隨時提取、簡單和諧的基本圖形分析法，自然流暢和快捷有效，由此成為學生的自然解法.

[1] 王堯興.一個數學模型的中考情結[J].數學教學，2013(10)：37-41.

[2] 蔡衛兵.在基本圖形的導航下進行合理思考[J].中學數學，2016(6)：51-55.

O123.1

A

1003-6407(2017)10-13-04