“互聯網+”時代農村物流配送中心選址的優化方案設計

楊葉勇

基金項目：江蘇省教育廳哲學社會科學研究基金資助項目“蘇南地區應急物流供應鏈的構建與運行機制研究”（批準號2013sjb6300091）；職教類青年專項課題“基于雙維視角的‘現代學徒制參與者研究”（課題編號SYKJ15D14）

中圖分類號：F252 文獻標識碼：A

內容摘要：本文簡要概述了農村物流配送中心選址的內容及原則，對物流配送中心選址的目標以及選址決策流程進行具體分析，基于成本最小化視角設計了農村物流配送中心選址的優化模型。在此基礎上，利用啟發式算法對運行步驟進行細致分析，最后使用案例算法得到農村物流配送的最佳選址方案。

關鍵詞：“互聯網+” 農村物流 配送中心 選址 模型設計

“互聯網+”時代下農村物流配送中心選址要義、目標與決策流程

一般而言，“互聯網+”時代下農村物流配送中心選址應遵循以下基本原則：第一，經濟性原則。農村市場經濟潛力巨大，流通企業在入駐農村規劃配送中心選址時，以盈利性為基本原則，即綜合考量費用的最低成本。這類成本包括了設施成本、交通工具與運輸成本以及倉儲等費用。同時，物流配送中心選址的確定位置，對之后配送時間、服務質量都會產生較大影響。因而，遵循經濟性原則規劃配送中心選址，能夠更好地開展農村市場的競爭。第二，適應性原則。在農村區域規劃物流配送中心，還應與當地的政策、物流運輸等方面結合，與當地技術發展水平、區域分布情況以及交通運輸承載力等協調統一發展。第三，戰略性原則。選擇最佳的物流配送中心，需要從農村區域的大物流系統出發，遵循當地整體發展戰略。特別是在“互聯網+”時代背景下，需要從全局層面考慮，局部服從整體，短期利益服從長期利益，為拓展農村市場奠定基礎條件。

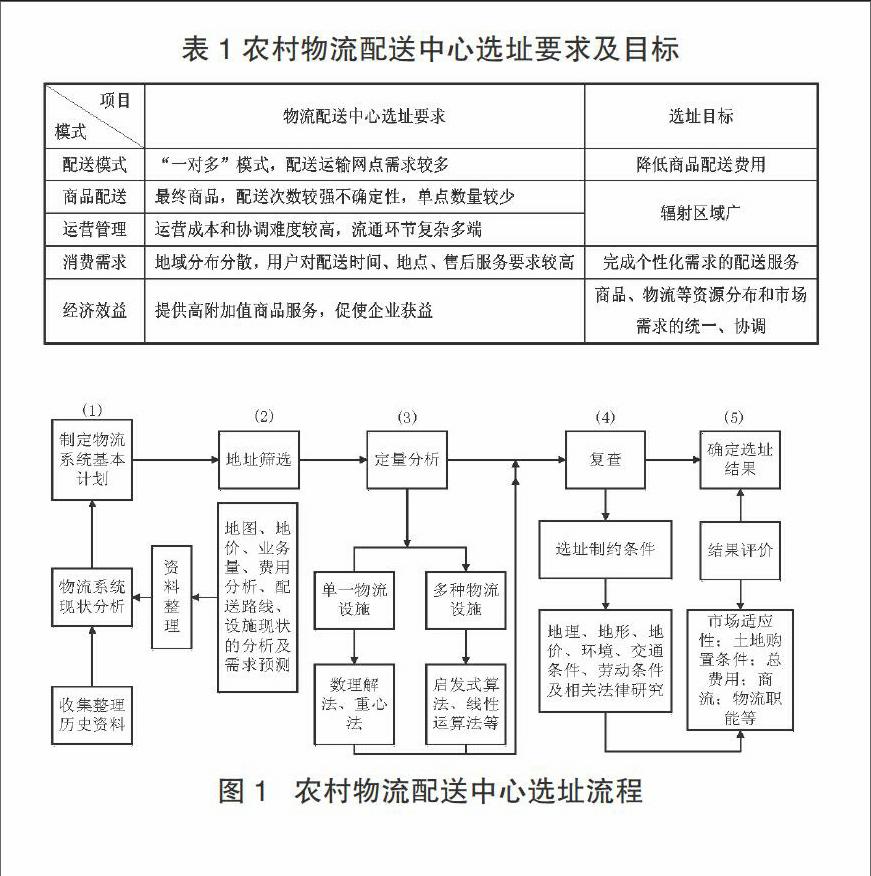
農村物流配送中心是聯系城鄉商貿流通的重要節點，其運作模式特征在于它并不是以商品生產為運作的社會組織，而是從各類生產商、批發商等手中匯聚商品資源，然后進行分類、配送等集約化的行為，進而實現最合理的利用物流網絡資源、降低商品流通成本的目的。因而，受農村交通運輸條件、商品資源分布以及市場需求因素的影響，農村物流配送中心的選址規劃設計在同一區域不同節點、不同的布局方案，所產生的經濟效益與社會效益可能會有較大的差異。合理布局選址方案的最主要目標在于，為用戶提供高質量、全方位的周到服務，降低流通成本，進一步實現社會效益與經濟效益的協調與統一。所以，商家在農村物流配送中心選址過程中（見表1），應根據配送模式、配送物品、組織管理、顧客需求以及經濟效益的選址要求，實現與之對應的目標即流通費用較低、服務質量水平較高、輻射區域廣泛以及社會效益高等。其中，流通費用低包括在規劃物流配送中心選址時，考慮到基礎設施成本與運營成本的總成本最低；服務質量水平較高是指所選的物流配送中心，應保證配送商品及時、完好地送達客戶；輻射強及社會效益高是指農村物流配送中心選址應從所選區域的物流大系統出發，使得選址區域的物流資源與市場需求、商品資源分布能夠達到高度協調與統一，適應地方經濟發展的實際情況。

選擇合理的農村物流配送中心地址，能夠最大限度降低流通企業成本、提升經濟效益。配送中心選址的決策過程主要包括以下幾個環節（見圖1）：首先，決策者通過收集整理歷史資料，分析當地物流系統現狀；經過資料整理，細致分析當地地價、業務量、費用、配送路線、設施現狀等資料，進而開始定量分析，由此制定物流系統基本計劃。其次，在對配送中心選址時，還應進行算法科學評估。若對單一配送中心進行選址，可采用數理解法、重心法；而針對多個配送中心進行選址時，可采用啟發式算法、線性運算法等。再次，決策者選出最佳選址算法時，需要進一步對所得結果進行復查。復查就是要對農村物流配送中心的選址約束條件進一步細分。此時，決策者應明確建立配送中心成本高低、必要性，還應根據物流系統基本計劃，確定所需要了解的基本條件，包括地理環境、交通條件、勞動條件、相關法律等，以縮小選址范圍。在此基礎上，對上述影響因素賦予一定權重，并使用加權算法對結果進行計算、核查。如所得數值通過核查步驟，那么該選項為最佳選址之一；如不符合原計算結果，需要返回上一步驟重新運算，直至循環結果同一。最后，需要決策者綜合服務質量、市場生產與消費資料、土地價格等，對所得結果進行評價，考察其可行性、現實意義及實用性，進而得到最佳的農村物流配送中心選址。

農村物流配送中心選址的優化模型構建

農村物流配送中心選址是否合理，將直接影響到農產品配送活動是否高效。科學合理建設配送中心，不僅可降低配送中心運營成本，還可推動商品產銷間的最佳協調，進而保持商品流通渠道的暢通。在分析農村物流配送中心選址的決策流程基礎上，還需運用模型理論與實際案例進行具體探討。因而，本文將總費用最低化作為基本目標，綜合考慮農村物流配送中心位置、倉儲、交通等因素，進行了其選址最優化模型目標函數的構建。

（一）模型基本假設與變量選取

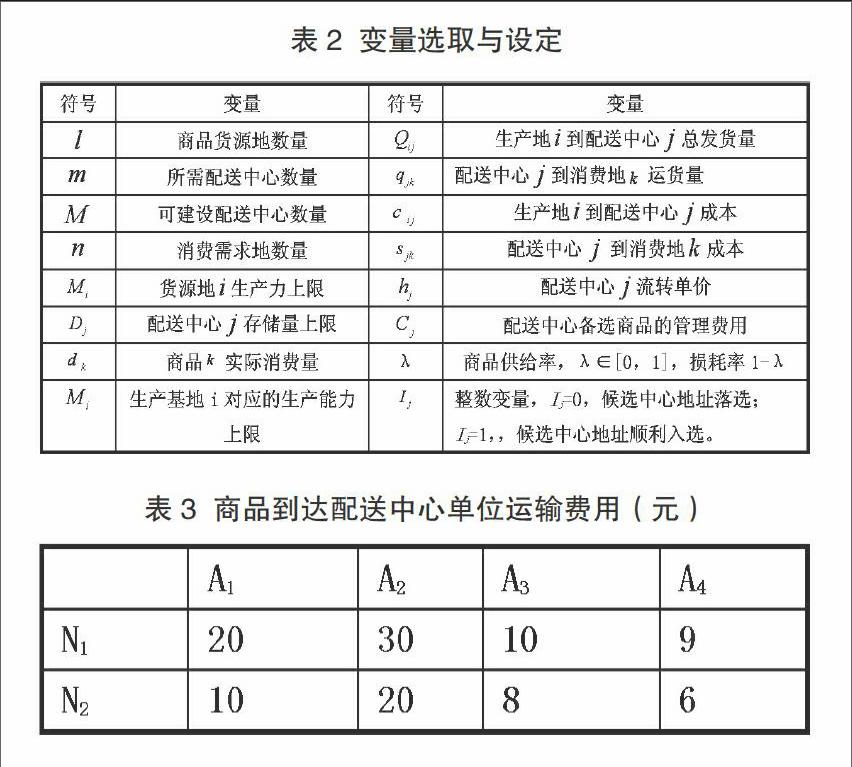
現進行如下假設：選定若干農村物流配送中心的候選區域，并在選定區域內進行最優篩選；只有一個物流配送中心提供消費市場區域的已知需求量；已知商品在農村地區的運輸費用，且運送地和配送中心之間距離和運輸費用呈正比關系；假設在”互聯網+”環境下，候選配送中心的基礎設施費用、運營管理費用已知；假設運輸速度為常量，且已選定的農村商品物流配送中心總體容量能夠有效滿足該區域的消費需求。同時，區域內的消費需求數量可以根據統計分析，即需求量是一個預測的外生常量。基于此，本文設定變量如表2所示。

（二）模型構建

從系統成本的最小化視角出發，設立“互聯網+”時代下農村物流配送中心選址成本最小化模型構建，即：

（1）

公式（1）中，所包含的約束條件如下：第一，， i=1，2，…，l， j=1，2， …，m，該公式所要表述商品生產地受到實際生產能力的約束。商品貨源地數量（l）與生產地到配送中心總貨量的總和數量，要小于商品基地對應的生產能力的上限。在此條件下，商品數量的配送可與當地消費需求數量達到平衡狀態。第二，，j=1，2， …，m ，該公式所要說明的是，商品配送中心j容量建設約束。即配送中心數量（m）與配送中心（j）到消費地（k）運貨量的乘積，也就是總貨量與商品生產基地對應生產能力的上限做比較。如超出這個能力，則不適宜將該地區作為物流配送中心。第三， ，j=1，2， …，m ，在考慮到商品配送中心供應能力時，配送中心數量（m）與配送中心（j）到消費地（k）運貨量的乘積，與商品實際消費量（k）作比較。正常情況下，配送中心商品總貨量應稍大于或等于實際消費需求量，才可以滿足當地區域的消費需求。第四，，j=1，2， …，m ，在考慮商品配送中心建設數量時，配送中心數量（m）與整數變量（Ij）的乘積，與可進行的農村物流配送中心數量作為比較。只有當前者小于或等于可建設的配送中心數量時，該地區入選作為配送中心才有最大的社會經濟效益。第五，當上述約束條件滿足 Qij≥0， qjk≥0， cij≥0，sjk≥0 ，且相應變量限定于條件 i=1，2，…，l， k=1，2，…，n，j=1，2，…，m 時，成本最小化（Cmin）模型運算才真正有意義。endprint

（三）模型的運算與求解

傳統算法中，NQ-difficult是一種無法獲得精確解的問題，而配送中心選址優化模型的求解過程過于復雜，類似于該問題的解答。為此，需要借助一種更為精簡的算法，更好對農村物流配送中心選址模型進行運算與求解，此時的啟發式算法成為比較好的選擇。具體來說，設定在m個候選區域內每次所選的結果組成N個組合集，即 CNm。在該集合中，包括候選區域的配送中心下標集合為V。隨后，應用啟發式算法對農村物流配送中心組合情況進行求解，將每個組合集討論完后，計算終止。具體算法步驟如下：

Step1：let U=V。計算出組合集中候選區域的中心容量上限為 ；鑒于配送中心容量上限需要滿足該區域的消費需求，還需要驗證與比較情況，如若前者大于或等于后者，那么該條件滿足，組合進入下一步的運算；否則刪除該組合，繼續分析下一組。

Step2：計算， J={jmin[cij+sjk]}，j∈U

Step3：利用單純形方法求解下列線性規劃問題：

目標函數： （2）

約束條件：

（3）

利用圖上作業法在約束條件（3）的情況下，對目標函數（2）進行運算，獲得線性規劃的最優解：

{Qij+qjk}（ i=…l； j=…m； k=…n） （4）

Step4：求解農村物流配送中心j配送容量 Qi=∑Qij， j∈U分析是否滿足 λQj≤Dj，j∈U條件，如若滿足，進行下一步；不滿足則刪除該組合，分析下一組合。

Step5：let U=U-1，直到出現U=φ結果，該運算結束。在U=φ結果的條件下，選擇出符合條件的組合，對之求解，獲得Cmin對應值。所選組合即為成本運行最低、配送服務質量較高以及社會經濟效益最大化的最終結果。

（四）選址模型的仿真案例

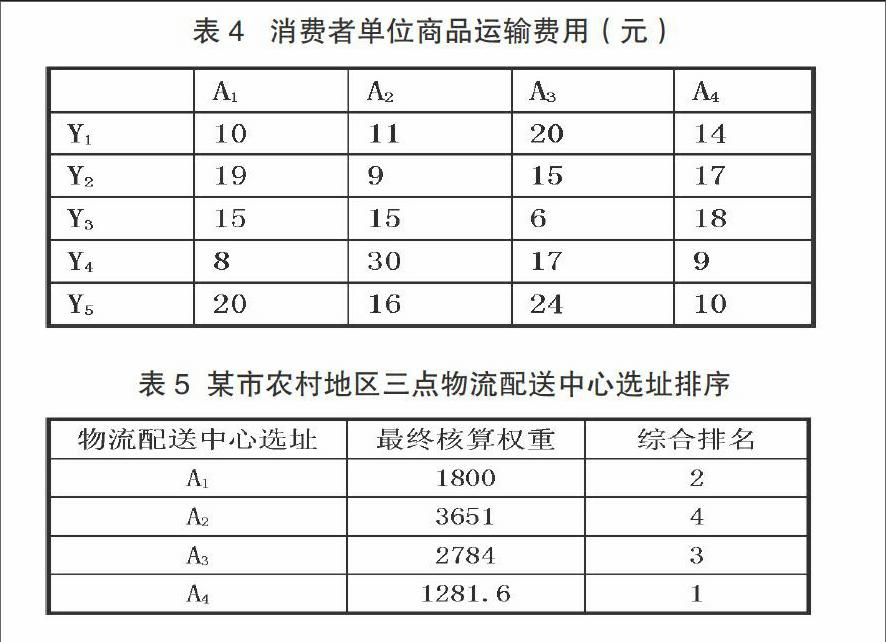
假設，N1和N2為兩個不同的商品貨源地，其日供貨量分別為70噸和50噸，可分別供應5個消費區Y1…Y5，并假定其貨物需求量為固定數值。商品貨源地周邊則存在4個物流配送中心以供選擇，分別為A1…A4，其建設費用分別為100萬、80萬、120萬、160萬，存儲最大量為50噸、40噸、60噸、80噸，商品的流轉單位為10元/噸、15元/噸、8元/噸、6元/噸。所建物流配送中心的單位商品流轉量成本，是依據該物流中心最大存儲量和其建設費用比來計算，并在商品貨源地和消費者之間進行流轉。其中，農村物流配送中心的選址關鍵在于，能否利用最佳計算機編碼進行選擇。在本算例中，有4個物流配送中心、2個供應商與5個消費區，只在4個候選區域中選擇一個目標作為配送中心。故本算例規模較小，在計算商品到達配送中心的單位運輸費用時，可采用二進制編碼運算。通過以上假設并運算得到表3單位運輸費用值，在N1和N2兩個貨源地到4個配送中心運輸費用大小為：A1>A2>A3>A4。

同理，商品經由配送中心到達消費者手中的單位運輸費用則如表4所示，A1、A2、A3、A4與Y1、Y2、Y3、Y4、Y5的對應費用所得比較為：72、81、82、68即A4

最后，依據上述A1、A2、A3、A4案例，依據最終權值矩陣得到最終核算權重：

A1點總成本：0.1*20*10*10+0.22**20*10*10+0.25**20*10*10+0.33**20*10*10=1800

A2點總成本：0.2*30*20*11+0.23*30*20*9+0.25*30*20*15+0.2*30*2*5=3651

A3點總成本：0.4*10*8*20+0.3*10*8*15+0.5*10*8*6+0.4*10*8*17=2784

A4點總成本：0.2*9*6*14+0.1*9*6*22+0.15*20*6*26+0.2*9*6*9+0.2*19=1281.6

將最終所得總成本順序進行排序，得到表5結果。通過表3、表4計算數值以及表5的選址排序可知，A4綜合優先級排名最高。因而，選擇A4為農村某區域物流配送中心選址的最佳方案。具體而言，經過對某市農村地區四點位置的最小成本模型、啟發式算法、仿真案例運算分析發現，農村物流配送中心選址應綜合配送中心到消費區域的運輸費用、消費者單位商品運輸費用以及綜合經濟效益的變量進行考量。在算例驗證過程中，A1、A2、A3、A4四個地區總得分比較，最終核算權重分別為1800、3651、2784、1281.6。可見，A4點最終權重得分較為明顯，成為最后選址的最佳地點。由此判斷發現，本文所采用的算法過程所得結果，與前文最小化成本演算理論結果相近，進而也進一步驗證上述成本最小化算法的可靠性。

參考文獻：

1.馮佳.基于C2C電子商務模式的農村物流發展體系構建[J].商業經濟研究，2015（8）

2.李鵬.流通配送中心選址的模型研究——以生鮮食品為研究對象[J].商業經濟研究，2016（12）

3.張婷婷.有競爭的物流配送中心選址模型研究[J].物流科技，2014（11）