例談小學(xué)英語復(fù)習(xí)課的教學(xué)

任艷

Lesh 提出與數(shù)學(xué)學(xué)習(xí)有關(guān)的五種表征，即“實物、教具模型、圖形、語言與符號，其中前三個表征較為具體，后二個表征較為抽象”[1]。用畫圖方式呈現(xiàn)問題，或在文字題上附加圖畫，是教科書及實踐中教師經(jīng)常采用的一種解題表征方式，這種以視覺手段表征知識的方式，即稱之為可視化表征，它能將文字題當(dāng)中的數(shù)量關(guān)系可視化、具體化。Van Hiele認(rèn)為，利用可視化的表征方法有降低思考層次的效果[2]。在小學(xué)高年級階段，許多問題都是以文字的形式來表征的，因其較為抽象，大多數(shù)學(xué)生尚停留在具體思維階段，問題理解存在一定的困難，而線段圖表征具有內(nèi)在負(fù)荷相對較低的特點，因此成為利用可視化表征解題的良好載體。筆者以線段圖為例，提出運用可視化表征的文字與圖形整合的教學(xué)模式，即把問題情境以線段圖示表現(xiàn)出來，通過線段圖輔助學(xué)生建立一個數(shù)量關(guān)系的心智模式，進(jìn)而克服文字閱讀的困難，降低學(xué)生理解問題的思維負(fù)荷，增加其在“問題解決”的過程中體驗成功的機會。

一、作線段圖表征問題

教材中的例題和習(xí)題，一般鮮有明確給出線段圖的。線段圖有兩種表征方式：無單位的線段圖和有單位的線段圖。研究所指的線段圖是有單位的線段圖，即用二條線段表示題目中各個數(shù)量間的關(guān)系。教學(xué)實踐中，當(dāng)學(xué)生閱讀題目文字時，可能無法理解題目所描述的數(shù)量關(guān)系，因而難以建立一個適當(dāng)?shù)男闹悄Ｊ剑€段圖作為外部表征可以嘗試引導(dǎo)學(xué)生去建立此數(shù)量關(guān)系的心智模式。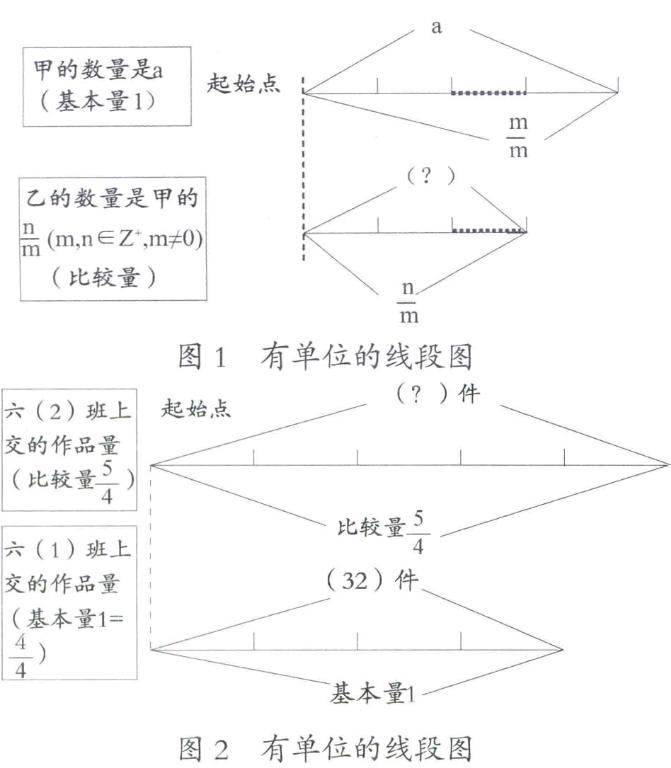

當(dāng)個體面臨問題時，會在腦海中或在紙上呈現(xiàn)與問題有關(guān)的圖像，以幫助個體進(jìn)行解題思路的可視化表征[3]。關(guān)于線段圖表征，教學(xué)中應(yīng)給學(xué)生厘清：圖中每一條線段表示什么；線段的單位數(shù)量能否體現(xiàn)出問題中各個量的數(shù)量關(guān)系。線段圖表征方式具體，而且易于體現(xiàn)數(shù)量間的倍數(shù)或比例關(guān)系。如圖1所示。

在小學(xué)階段，遇到難度較高的分?jǐn)?shù)問題（例如分?jǐn)?shù)乘法、除法、異分母分?jǐn)?shù)加減等問題）時，適宜引入線段圖來表征這些問題，它可以有效地消解因過多的元素互動造成認(rèn)知負(fù)荷過大的情形。另外，用單位長度表征可以進(jìn)行多次的具體等分及合并活動，實踐中可保留這些活動的痕跡，其優(yōu)點在于：一方面，這些具體操作活動是進(jìn)一步抽象思考的基礎(chǔ)，另一方面，保留具體活動痕跡更易于監(jiān)控解題過程及反思解題過程。

二、確定基本量與比較量，找出（計算）比例關(guān)系

線段圖表征需要先確定一個元素作為單位，然后以該單位作為新的測量標(biāo)準(zhǔn)，此單位即基本量，再以基本量來詮釋別的元素，即比較量。表征問題情境的線段圖用基本量來刻畫，即線段圖的單位。

三、依據(jù)比較量與基本量的比例關(guān)系，畫出二條并排線段圖

學(xué)生對文字信息進(jìn)行語意處理，一般情況下，都需要納入長時記憶區(qū)中的認(rèn)知結(jié)構(gòu)來理解，即以其已有的認(rèn)知結(jié)構(gòu)為基礎(chǔ)。但是在問題解決的特有情境下，學(xué)生可能不能及時觸發(fā)其適當(dāng)?shù)恼J(rèn)知結(jié)構(gòu)來進(jìn)行概念組織。因此，需要對問題中的文字?jǐn)⑹鲞M(jìn)行恰當(dāng)?shù)拿}表征來輔助學(xué)生建構(gòu)心智表征，進(jìn)而促進(jìn)學(xué)生理解題意。

對于小學(xué)高年級學(xué)生而言，均已具備一定的空間意義和認(rèn)知體驗。因此，可采用可視化的線段圖表征命題，以直觀的線段圖來表征元素間的相互關(guān)系。表征的意義在于利用學(xué)生長時記憶區(qū)中的認(rèn)知結(jié)構(gòu)引導(dǎo)其進(jìn)行模式建構(gòu)與模式識別的活動。模式建構(gòu)是指利用線段圖來表征兩個班級上交作品數(shù)量的大小關(guān)系，模式識別是指這兩條并排的線段能否恰當(dāng)?shù)乇憩F(xiàn)兩個班級上交的作品的數(shù)量關(guān)系。因此，可畫起始點相同、二條并排的線段圖，即描繪性表征，以此來比較兩個量之間的相互關(guān)系。

兩個班級上交作品的數(shù)量間關(guān)系不僅可以用來分析文字與圖象的理解，也可以用來研究從外部表征——可視化的線段圖表征來建構(gòu)內(nèi)部表征——心智表征的過程。這種外部表征可以用來溝通、分享知識的習(xí)得，如實踐中教師會通過線段圖來輔助講解題意，學(xué)生也可將產(chǎn)生的外部表征視為認(rèn)知工具來輔助問題解決，即可以依托線段圖載體思考兩個量之間的相互關(guān)系，同時將問題解決過程中所需的認(rèn)知需求反映到線段圖當(dāng)中。

四、依據(jù)線段圖，列式解決問題

在畫線段圖的過程中，線段圖表征與心智模式會持續(xù)地產(chǎn)生交互作用，進(jìn)而促使學(xué)生對文字和圖象所要表達(dá)的意義理解得更清晰、更深入，并在理解的過程中不斷修正和完善學(xué)生建構(gòu)的心智模式與命題表征。如引導(dǎo)其認(rèn)知結(jié)構(gòu)進(jìn)行模式檢測——線段圖能否準(zhǔn)確體現(xiàn)文字表達(dá)的數(shù)量關(guān)系。學(xué)生在描述性表征和描繪性表征的互動過程中，借助線段圖的輔助，完善心智表征，提取有效信息，正確列式，進(jìn)而正確解決問題。

六（1）班上交作品為基本量時，數(shù)量是32，每個單位格是32÷4=8 （件），六（2）班上交作品量是8×5=40 （件）。所以兩個班級一共上交作品：32+40=72 （件）

答：兩個班級一共上交作品72件。

線段圖作為一種常規(guī)的可視化表征手段，教師引入其表征解題策略的目的不僅僅是解題，更多的因素是期待學(xué)生能夠理解表征背后所表達(dá)的關(guān)系，進(jìn)而從表征所建立的模式中提取出新的信息，以此實現(xiàn)問題解決的目的。

值得一提的是，教學(xué)模式中元素間的關(guān)系通常是以“比較量÷基本量=比值”來表達(dá)，即“比與比例”。現(xiàn)今各版本的小學(xué)數(shù)學(xué)教科書中，對“比與比例”內(nèi)容，采取不同的呈現(xiàn)方式和邏輯結(jié)構(gòu)，教師可將線段圖作為理解分?jǐn)?shù)解法的輔助工具，讓學(xué)困生也能掌握整數(shù)乘除與分?jǐn)?shù)乘除解法之間的關(guān)系，提升學(xué)生在“比與比例”單元學(xué)習(xí)成功的機會。

總之，可視化表征可以使得研究內(nèi)容更直觀化、關(guān)系更具體而清晰，而且能夠“幫助他人正確地重構(gòu)、記憶和應(yīng)用知識”[4]。可視化的線段圖表征目的在于把問題情境以可視化的方式表征出來，并通過線段圖提升學(xué)生的列式和運算能力。因此，可視化表征是輔助學(xué)生“怎樣解題”的一種有效而且高效的教學(xué)工具。

參考文獻(xiàn)

[1] Grouws D A.Handbook of Research on Mathematics Teaching and Learning[M]. New York：Macmillan Publish Company，1992.

[2] Van Hiele，P.M.Structure and insight[M].New York：Academic Press，1986.

[3] 王寬明.可視化表征在工程問題中的應(yīng)用[J].教學(xué)與管理：小學(xué)版，2016（3）.

[4] 邱楊，高榮國.以知識可視化表征改善學(xué)習(xí)內(nèi)容的呈現(xiàn)[J].江蘇教育學(xué)院報，2007，24（4）.

[責(zé)任編輯：陳國慶]endprint