在學習中成長　在教學中提升

羅純潔

新課程標準倡導的核心教學理念是“以學生發展為本”，這就需要我們教師重新認識自己的角色，教師從知識的“傳授者”轉變為學生學習的促進者，教師不再是“教書匠”，而是一批擁有先進教育觀念、懂得教學反思技術、善于合作的探究者.只有不斷學習，不斷在課堂教學中磨練，教師才能進一步發展，實現自我提升。

在數學學習過程中，學生常常會出現“能聽懂，做不來”的現象。究其原因，我想這與我們的教學方式不無關系。在日常教學中，教師有時會急于求成，把一些解決問題的方法和盤地教給學生，學生吃的是現成飯，學得快，忘得也快。這種教學，忽視了對知識的產生、發展、形成和應用過程的揭示和探究，不善于將這一過程中豐富的思維訓練因素挖掘出來，也不善于將知識中蘊藏的豐富的思想方法加以暴露，學生的解題能力就不能得以很好的培養。怎樣才能改變這種狀況呢？《數學課標》指出：“有效的數學學習活動不能單純地依賴模仿與記憶，動手實踐、自主探索和合作交流是學生學習數學的重要方式。”我校的四導四學教學方法正好體現了新課標的教學模式。

下面我以一節課的教學為例談談我在教學中的一點體會：

在《等腰三角形》一課的教學中我力求讓學生經歷知識的形成過程，調動學生原有的知識和生活經驗，通過動手操作來發現新問題，并注意引導學生通過觀察、實驗和操作，突出體現了學生對知識的獲取和能力的培養，并在這個過程中注意了以下幾點進而培養了學生學習興趣，發展智慧，增長才干。

一、導入新學

在實踐體驗中激發學生興趣。心理學家布魯納認為：“學習是主動的過程，對學生學習的內因的最好激發對所學材料的興趣，即主要來自學習活動本身的內在動機，這是直接推動學生主動學習的心理動機。”教學中，我讓學生親自動手制作等腰三角形，然后讓學生說明一下自己為什么這樣制作等腰三角形，你為什么就認為你做的這個三角形就是等腰三角形呢？這樣就使學生個體全身心地置身于真實的數學活動中，切身感受數學的實用性，導入了新課，體會學數學的快樂，同時也為本節課后面學習的重點內容打下堅實的基礎。

二、指導自學

獨立思考與合作交流有機結合。學會思考與交流是現代社會所必須的，也是數學學習過程中應當提倡的組織形式。建立平等、民主、友愛的師生關系，創設和諧、寬松的課堂氛圍，是學生主動探究的前提條件。本課中，我為學生提供了比較開放式的探索材料：讓學生把在上一個環節中自己制作的等腰三角形剪下來，然后對折，讓兩腰重合在一起，觀察自己手中的等角三角形模型，然后去思考問題，你會得到一些什么樣的結論，請盡可能多的寫出來。這樣，就讓學生在自然的情景中，在教師的幫助下，自己動手，動腦“做數學”，用觀察、模仿、實驗、猜想等手段收集資料，獲得體驗，調動了學生主動參與的積極性，在鼓勵學生獨立思考的基礎上，進行合作交流，學生很快會回答出“兩個底角相等”“這條折痕是頂角的角平分線”“這條折痕是底邊上的高線”等等，從學生回答問題的情況看出，有些結論盡管對這節課實際意義不大，但說明學生有所思、有所得，真正參與到教學活動中來了，有效地培養了學生的自學能力。

三、引導互學

建立良好的師生互動關系。教師作為課堂教學的主導，任務是激發學生自己去學習、去研究，并與學生一起做數學。本課中，盡量采用“問題—思考—交流—總結”的模式展開，啟發學生自主研究、合作探究來解決問題。做到教師只是一個組織者和引導者，教師的責任更多的應該是為學生提供思考的機會和平臺，為學生留有思考的時間與空間，而不是急于下結論。

在這個環節教師應適時的巧妙滲透數學思想方法。學生掌握了數學思想方法，就能從本質上把握數學，優化數學思維品質，使學生獲得終生受益的東西。新課標強調：“在教學中，應當引導學生在學好概念的基礎上掌握數學的規律（包括法則、性質、公式、公理、定理、數學思想和方法）”。本課中，對于等腰三角形的性質“等邊對等角”的由來是先讓學生動手操作再進行幾何推理證明，其實質是特殊到一般、具體到抽象的數學思想方法的體現。如例1，已知：在△ABC中，AB=AC，∠B=800，求∠C和∠A的度數。和拓展例1，已知：在△ABC中，AB=AC，∠A=800，求∠B和∠C的度數。最后小結：在等腰三角形中，已知一個角可以求出另外兩個角， 滲透了類比歸納的數學思想方法。從“例1”到“例2”又滲透了分類討論的數學思想方法。數學教育不僅要關注學生對數學知識的獲取，更應關注學生的思維和一般能力的發展，這不只是學生學習數學有用，而且對于學生將來步入社會做任何事情都是有價值的。因此在數學學習中必須為學生進一步發展提供必需的基礎知識和思想方法，更充分體現了引導互學這個教學環節的重要性。

四、輔導固學

讓學生在問題的解決中學會一題多解、舉一反三。本節中對于等腰三角形的性質的證明引導學生討論出三種方法（關鍵是如何作輔助線），例題、變式訓練不僅向學生展現了數學的嚴謹性和邏輯性，而且也體現了一題多解、舉一反三的思想方法。

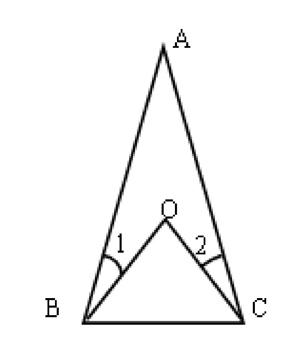
如：已知：如圖，O是△ABC內一點，AB=AC，OB=OC，求證：∠1=∠2

學生討論分析出兩種方法：方法一：利用等腰三角形的性質;方法二：利用全等三角形的判定。本節課在習題的搭配上也體現了層次，為各類學生創造了提高的機會。

通過這樣的課堂實踐，我領悟到四導四學的教學理念，學生進行“自主學習、合作學習”的學習方式的益處，也真正體會到學生的潛能所在。我也從中得到了鍛煉，積累了課堂教學經驗。

教師的成長，在于不斷的學習，在于課堂教學的不斷實踐與反思。只有不斷學習經過課堂上反復實踐與課后的反思，教師的有效經驗才能上升到一定的理論高度，才會對后續的教學行為產生積極的影響。