一個數學問題的再加強

浙江省湖州市雙林中學(313012) 李建潮

一個數學問題的再加強

浙江省湖州市雙林中學(313012) 李建潮

《數學通報》2008年8月號問題1746是:設I是△ABC的內心,R是△ABC的外接圓半徑,r,r1,r2、r3分別是△ABC、△IBC、△ICA、△IAB的內切圓半徑.求證:

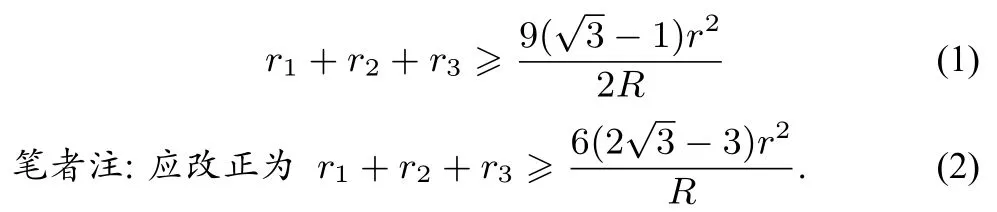
當且僅當△ABC為正三角形時等號成立.

命題人的證明推導出了

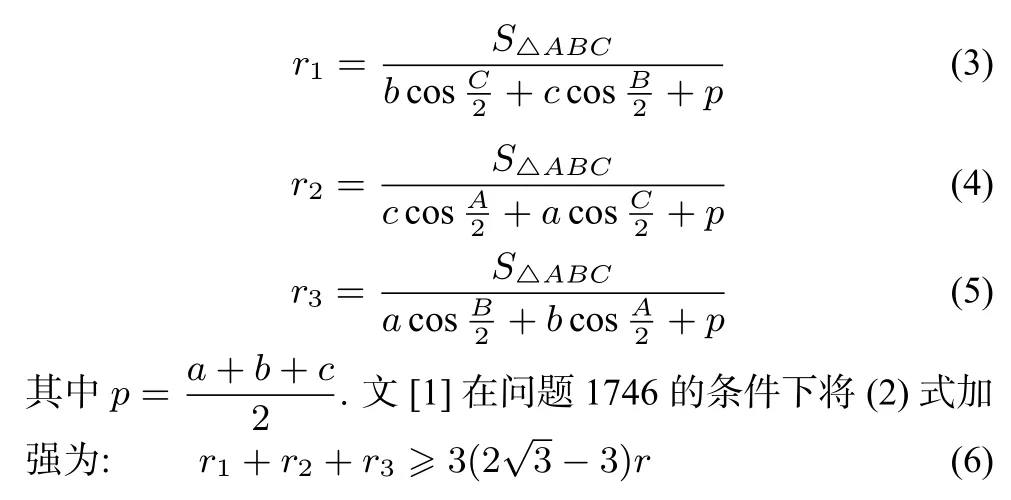
本文進一步給出(6)式的加強:

命題在數學問題1746的條件下,有

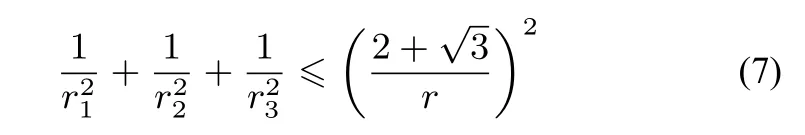
當且僅當△ABC為正三角形時取“=”號.

證明將二維柯西 (Cauchy)不等式 (ac+bd)2≤(a2+b2)(c2+d2)(當且僅當bc=ad時取“=”號)用于(3)式,并注意到射影定理a=bcosC+ccosB,有

(當且僅當B=C時取“=”號),同理可證:

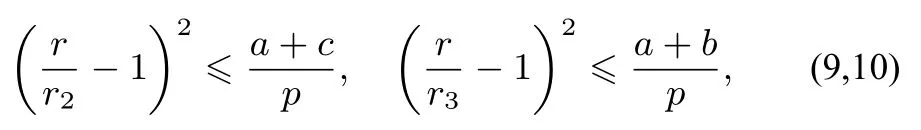
(當且僅當C=A,A=B時(9)、(10)分別取“=”號)(8)、(9)、(10)三式相加,得

其中(7)式取“=”號當且僅當△ABC為正三角形.

顯然,由以下不等式:

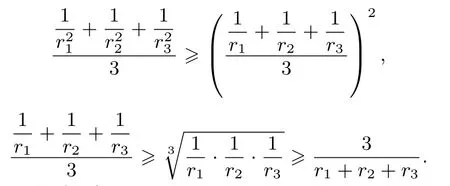
還可以得到:

推論在數學問題1746的條件下,有

當且僅當△ABC為正三角形時取“=”號.其中(14)式即為(文[1]的)(6)式.

[1]陳遠新,唐鴻.數學問題1746的加強[J].數學通報,2010,7.