山東省微山縣第一中學(xué)(277600) 朱廣軍

源于基礎(chǔ) 深入思考
——從橢圓焦點(diǎn)三角形談起

山東省微山縣第一中學(xué)(277600) 朱廣軍

一個(gè)頂點(diǎn)在橢圓上,另兩個(gè)頂點(diǎn)為橢圓焦點(diǎn)的三角形叫橢圓的“焦點(diǎn)三角形”.與“焦點(diǎn)三角形”有關(guān)的問(wèn)題可以綜合地考查三角形中的正(余)弦定理、面積公式及圓錐曲線的定義和標(biāo)準(zhǔn)方程等知識(shí).涉及焦點(diǎn)三角形面積、弦長(zhǎng)問(wèn)題多次出現(xiàn)在試題中,直接解答一般較復(fù)雜,若我們能合理而又靈活地運(yùn)用橢圓的焦點(diǎn)三角形的面積公式、焦半徑、焦點(diǎn)弦弦長(zhǎng)公式,在解決這類有關(guān)問(wèn)題時(shí),可避免冗長(zhǎng)的推理和運(yùn)算,大大降低難度,從而使問(wèn)題得以巧妙簡(jiǎn)單地解決.因此很有必要對(duì)橢圓的焦點(diǎn)三角形、焦半徑、焦點(diǎn)弦弦長(zhǎng)公式等問(wèn)題進(jìn)行系統(tǒng)地研究.

此結(jié)論在教學(xué)中重點(diǎn)講到,此處不再證明,只給出舉例應(yīng)用

點(diǎn)評(píng)一般方法運(yùn)用定義和勾股定理|PF1|2+|PF2|2=4,解得|PF1|·|PF2|=2,S△F1PF2=1.運(yùn)用面積公式大大簡(jiǎn)化了運(yùn)算過(guò)程.思考在結(jié)論1中,若已知∠PF1F2=θ,那么是否有類似的焦點(diǎn)三角形面積公式呢?經(jīng)過(guò)推理證明得到以下結(jié)論.

(2)證明與(1)相仿,從略.

點(diǎn)評(píng)利用結(jié)論2,可以省略復(fù)雜的思考過(guò)程,提高解題速度.在結(jié)論1及結(jié)論2的證明過(guò)程中得到以下橢圓的焦半徑公式的三角形式.

結(jié)論3 設(shè)橢圓方程左右焦點(diǎn)分別為F1,F2,點(diǎn)P為橢圓上一點(diǎn),PF1與x軸所成的角為θ,PF2與x軸所成的角為α,c為橢圓的半焦距,則

例3 設(shè)橢圓的左右焦點(diǎn)分別為F1,F2,過(guò)F1作橢圓的長(zhǎng)軸的垂線交橢圓于點(diǎn)P,若△F1PF2為等腰直角三角形,則橢圓的離心率為____.

點(diǎn)評(píng)例3根據(jù)公式可以直接計(jì)算三角形邊長(zhǎng)|PF1|,進(jìn)而得到a,c關(guān)系式,求出離心率.一般方法可以先求出點(diǎn)P坐標(biāo),再有兩點(diǎn)間的距離公式計(jì)算|PF2|.例4利用公式直接計(jì)算出假設(shè)滿足條件的兩個(gè)焦半徑長(zhǎng)度.再根據(jù)橢圓定義直接給出滿足條件的解的個(gè)數(shù).而一般方法通過(guò)勾股定理和橢圓的定義解得|PF1|=|PF2|=4.比較而言,我們的方法更為節(jié)時(shí)而精準(zhǔn).由結(jié)論3可得到過(guò)焦點(diǎn)弦的弦長(zhǎng)公式.

證明如圖(1),考慮AB所在直線傾斜角為直角或銳角且該直線經(jīng)過(guò)F1的情形,對(duì)于其它情形可以相仿地討論.由結(jié)論

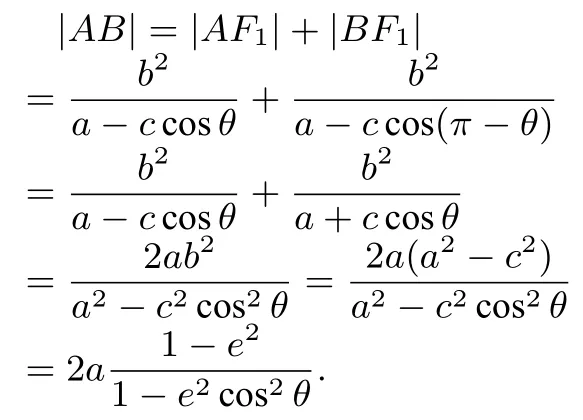
圖1

(1)求橢圓的方程;

證明如圖2,考慮AB過(guò)F1且θ為直角或銳角的情形,其它情形證明相仿.由結(jié)論 4得則焦點(diǎn)F2到直線AB的距離d=

圖2

點(diǎn)評(píng)以上例5—7都可以用聯(lián)立直線、橢圓方程組化為二次方程,利用根與系數(shù)、弦長(zhǎng)公式計(jì)算弦長(zhǎng)、點(diǎn)到直線的距離公式等知識(shí)點(diǎn)求解.但比較而言,這里給出的方法更為簡(jiǎn)潔.