在解法探究中賞析美題

浙江奉化高級中學(315500) 柴驥寧

在解法探究中賞析美題

浙江奉化高級中學(315500) 柴驥寧

一道好題,應該是其背景深刻豐富,但在解法優化過程當中又能呈現出“接地氣”且通俗易懂的通法,本文呈現一例,探究與挖掘一下其豐富的“源與流”.

題目呈現(2016屆東北三校第一次聯考理科第16題)已知在△ABC中點M是△ABC外一點,BM=2CM=2,則AM的取值范圍為____.

下面筆者主要通過對于這道試題多角度的解答,挖掘其豐富而又深刻的內涵.

分析首先對于這個向量等式的處理是簡單的,結合圖1,易知△ABC是等腰三角形,在由易得,△ABC為正三角形,接下去筆者來具體地解決這個問題.

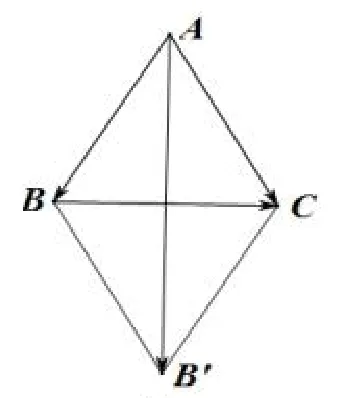
圖1

對于一個幾何題,特別對于考試中的學生而言,筆者認為,幾何代數化即建系法,是立竿見影,思維量極少的過程,重點在于計算能力,因此生成了下面的第一種解法.

解法1如圖2,建立平面直角坐標系,設B(?a,0),C(a,0),由M是外一點,易知a∈又由BM=2CM=2得到 (x+a)2+y2=4, (x?a)2+y2=1,兩式聯立解得點

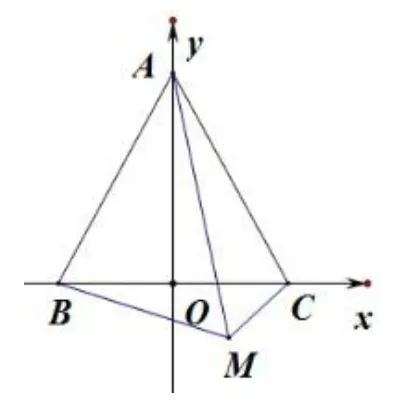
圖2

因此,

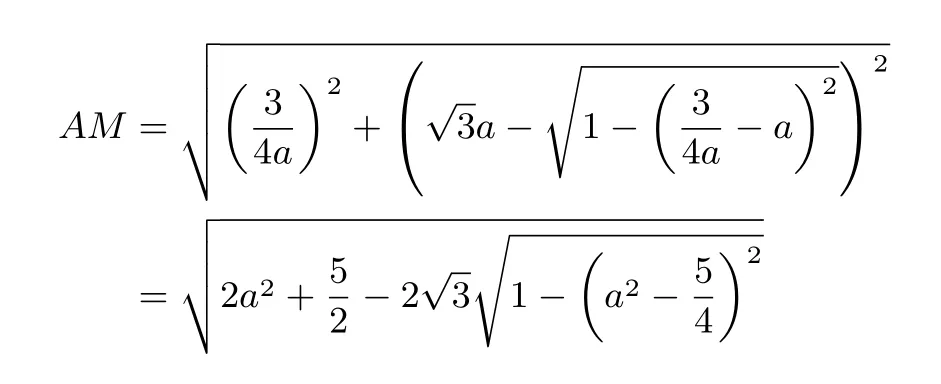
此法是通過建系,用代數化的方式解決幾何問題,該法利在思維量較小,而弊端是計算量大,對學生而言當屬具有可操作性且通俗易懂的好法子.不難發現解法1中有個三角換元的過程,因此有了解法2.

解法2如圖 3,以點M為坐標原點O,線段OB所在的直線為x軸建立平面直角坐標系,則設M(0,0),B(2,0),C(cosα,sinα)(α∈[0,2π))而向量可以看成是向量繞B點順時針旋轉60°而來,因此

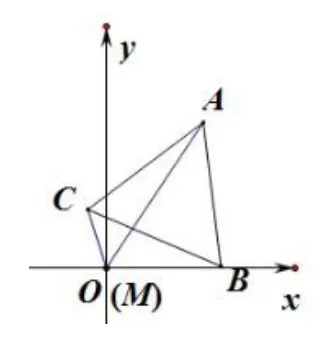
圖3

解法2對于減小計算量有了個質的飛躍,但是其中涉及了一個向量旋轉得到點的公式,雖說這個知識要點在必修四習題出現過,但對于學生而言有一定的陌生度.如果在解法2的建系方式上,改變進行坐標的三角設法,生成解法3.

解法3設C(x,y)則由BM=2CM=2易得x2+y2=1(y/=0),易知點C的軌跡為一個單位圓,而設A(x,y),進而得到A點軌跡方程為也是一個圓,進而得到如圖4,通過圖形易知AM∈[1,3].

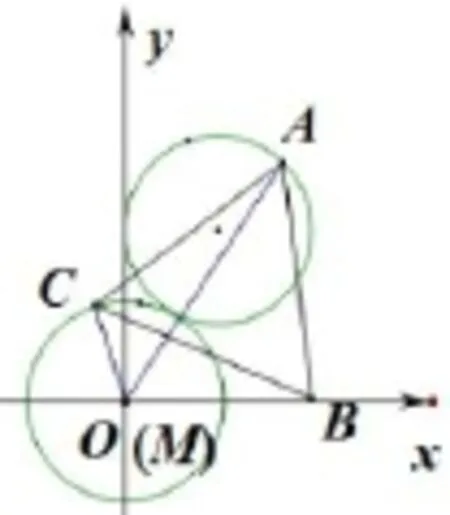
圖4

此法在解決A的軌跡方程上其實“阿波羅尼斯圓”,下面簡要說明.

阿波羅尼斯圓到兩個定點A,B的距離成定比(不等于1)的點的軌跡是圓.

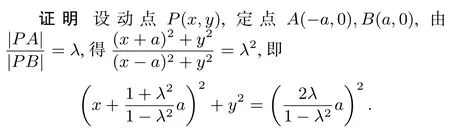
當λ＜1時,定點A在圓內部,定點B在圓外部;當λ＞1時,定點A在圓外部,定點B在圓內部.

在近些年的高考試題中對阿波羅尼斯圓多有涉及,篇幅所限,本文不再贅述.

上述的解法還是局限在解析法的范疇,其實我們還可以用平面幾何輔助線的方式解決本題.

解法4如圖5,將△ABM繞著點B順時針旋轉60°到△BCM′,連接MM′,從旋轉得到△BMM′為正三角形,則BM=MM′=2,AM=CM′,易知MM′+MC≥CM′,所以當且僅當M在線段M′C上時,AM取得最大值3.

如圖6,將△ABM繞著點C順時針旋轉60°到△BCM′,連接MM′,從旋轉得到△BMM′為正三角形,則MC=MM′=1,AM=BM′,BM′+MM′≥BM??BM′≥BM?MM′=2?1=1,,所以當且僅當M′在線段MB上時,AM取得最小值1;故AM∈[1,3].

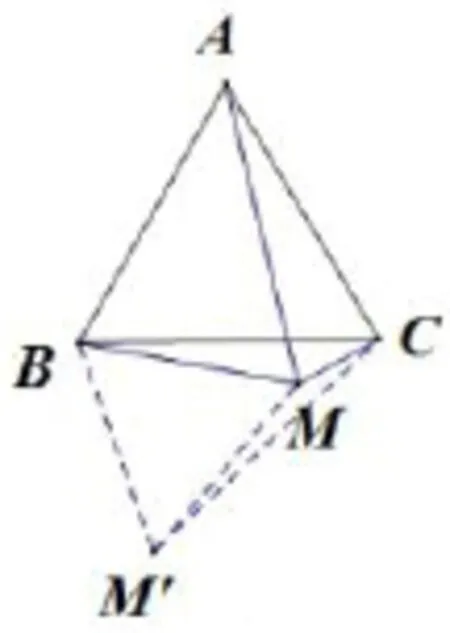
圖5

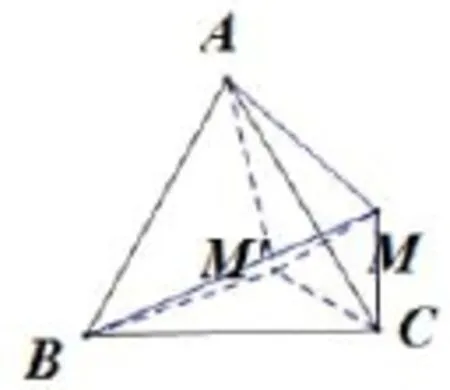
圖6

我們還可以用圓內接四邊形的性質解決問題.

解法5先引入一個如下引理,即托勒密定理:圓的內接凸四邊形兩對對邊乘積的和等于兩條對角線的乘積.此定理有個如下推論:任意凸四邊形ABCD,必有AC·BD≤AB·CD+AD·BC,當且僅當ABCD四點共圓時取等號利用推論,結合圖5,圖6,設AM=x,AB=AC=BC=a,易得如下不等式組當且僅當A,B,C,M四點共圓時取到等號.

此法同上一解法,都是從純幾何的角度給出解析和挖掘了,與此同時也找到了其深刻的幾何背景意義,以及一個托勒密定理的幾何應用.那么既然是一道有關三角形的題目,自然會有用解三角形那方面的知識去解決此題,因此生成了下面解法.

解法6如圖7,設∠BCM=α,∠BMC=β,AB=AC=BC=a,則在△BMC中,有如下結論:由正弦定理得到:

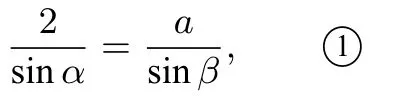
由射影定理得到:

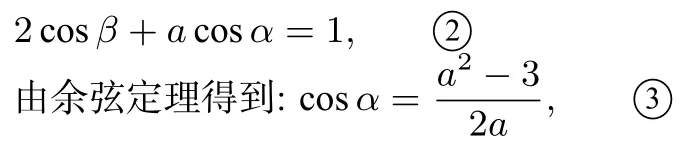
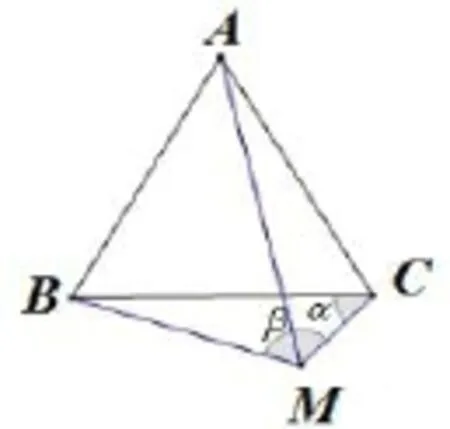
圖7

在△ACM中,由余弦定理得到:(注意到點M動點,可以在三角形的任意一側)

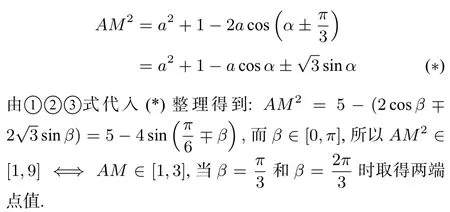
此法很好地利用的解三角形的知識解決了一個三角形問題,還設計到三角恒等變換,正可謂是把三角這個板塊公式來了一個大集結,雖是小題,但有知識點俱全,正如俗語“麻雀雖小五臟俱全”.上一解法是通過解三角解決問題,再消字母a轉換成三角函數求值域問題,那么同樣可以保留a,直接看成a函數求值域,因此生成了下面解法.

解法7還是借用圖7,只設∠BCM=α,AB=AC=BC=a,則在△BMC中由余弦定理得到:

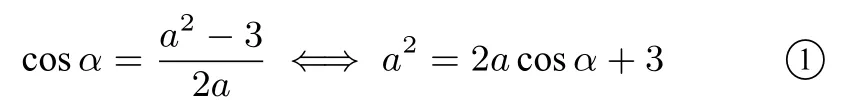
在△AMC中,又余弦定理得到

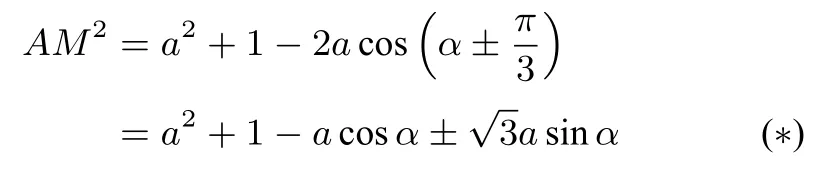
(?)式將①式代入,再將sinα,cosα由①式變形之后整體轉換成a的式子,得到

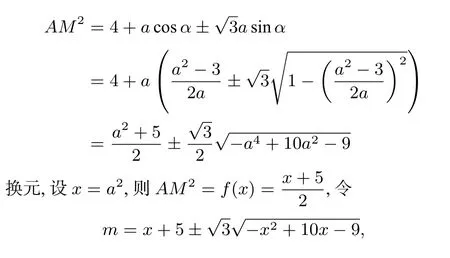
等式兩邊平方得到關于x的一元二次方程

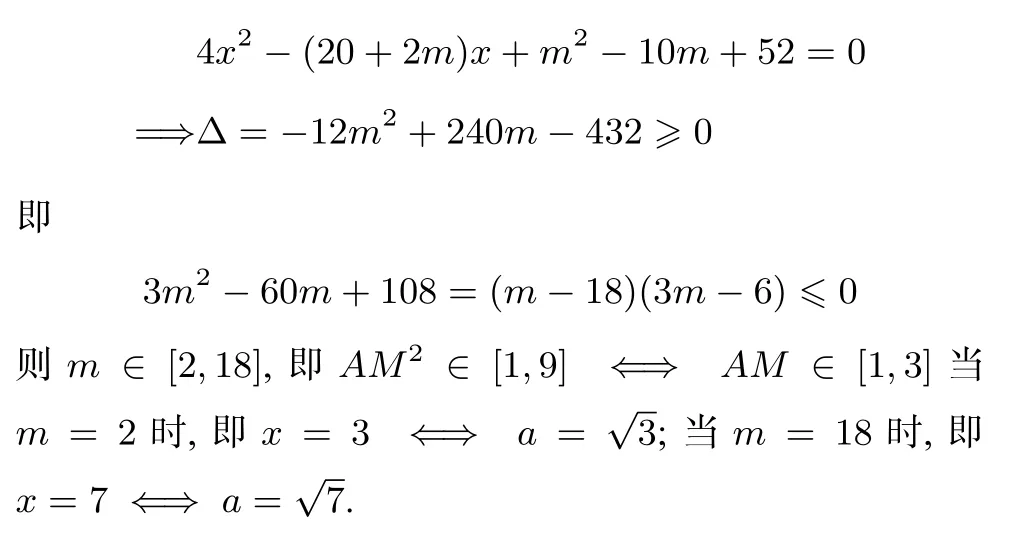
此法很好地展現了高中階段函數主線的影子,對于函數求值域的處理應該是靈活嫻熟的.

以上七種解法,可以分為三類解法,主要是解析法,純粹的平面幾何輔助線以及定理的應用,再者就是解三角形的處理方式.一個小題,它展現了其深厚的背景魅力,有阿氏圓以及托勒密定理,與此同時它也囊括了高中階段數學的許多思想方法和知識要點,并且在解法當中,筆者認為利用初中階段的三角形旋轉是最優且通俗易懂的方法.總之,一個題方法多種多樣,有通法通解,亦有巧解妙解,但是無論什么解法,對于解題者而言,選擇適合自己“氣質”的方法最佳,正如同每人的思維思考方式迥異.