無定子磁鏈觀測的永磁同步電機直接轉矩控制

鄭云廣,陸 可,謝建隆

(西南交通大學，成都 610031)

0 引 言

永磁同步電機(以下簡稱PMSM)具有體積小、效率高、功率密度大等特點，被廣泛應用于工業和交流傳動領域。PMSM直接轉矩控制(以下簡稱DTC)結構簡單，對電機參數依賴較小，魯棒性強等特點受到廣泛關注[1]。

傳統PMSM DTC利用6個有效電壓矢量，通過優選電壓矢量的方式對定子磁鏈和轉矩進行調節，利用磁鏈滯環和轉矩滯環形成雙閉環控制，以定子磁鏈的位置信號作為扇區判斷標準選擇開關表[2-3]。與矢量控制相比，電流解耦不徹底，磁鏈和轉矩波動較大。為了克服DTC中轉矩脈動較大等問題，有文獻提出通過將電壓矢量細分達到削弱轉矩脈動的目的[4]；文獻[5]通過分析滯環寬度對控制性能進行優化，獲得了較低的電流諧波含量。文獻[6]對不同策略下電流與磁鏈給定的關系進行研究，磁鏈計算不能避免，計算量較大。針對DTC中磁鏈波動較大的問題，文獻[7]引入模糊邏輯控制器代替滯環比較器，有效抑制了轉矩脈動，但仍需要對磁鏈進行實時計算。文獻[8]和文獻[9]基于有效電壓矢量優化的思想，分別提出電壓矢量評估因子和最小電壓矢量偏差的策略。文獻[10]提出了一種基于空間矢量調制的方法，但由于要對磁鏈差進行實時估算，計算較為復雜。傳統的直接轉矩控制往往建立在靜止的α-β坐標系下，僅靠定子磁鏈和電磁轉矩滯環控制，不能對三相電流進行徹底的解耦。因此當一個空間電壓矢量改變定子磁鏈時，沒有顧及對電流的影響。為了改善電流波形，往往通過磁鏈限幅或者其他磁鏈給定算法來實現[11]。

為了獲得良好的電流特性，同時保持DTC結構簡單，強魯棒性的特點，在傳統直接轉矩的基礎上，結合表貼式PMSM的特點，分析了PMSM電磁轉矩和6個有效空間電壓矢量之間的關系。在d-q坐標系的基礎上，分析電磁轉矩和電壓矢量之間的關系，選擇出能同時兼顧電流調節的優選電壓矢量，在調節電磁轉矩的同時達到電流的限制，保障電機穩定運行。

1 系統模型和傳統DTC

1.1 三相S-PMSM數學模型

取永磁體磁鏈方向為d軸正方向，在d-q兩相旋轉坐標系下的PMSM電壓方程：

(1)

三相表貼式PMSM轉矩方程：

(2)

式中：ud，uq分別為d-q坐標系下的d,q軸定子電壓；Rs為定子電阻；id，iq為d，q軸定子電流；ψd，ψq分別為d,q軸磁鏈;p為極對數。

PMSM運動方程：

(3)

式中:Te為電磁轉矩；Tl電機負載轉矩；J為電機轉動慣量；ωr為電機轉子機械角速度；RΩ為電機阻尼系數。

1.2 傳統DTC方案

傳統DTC系統采用磁鏈轉矩雙閉環，通過滯環比較器和查表的方式選擇合適的電壓矢量使電機磁鏈軌跡接近正六邊形或標準圓。其控制方案原理如圖1所示。

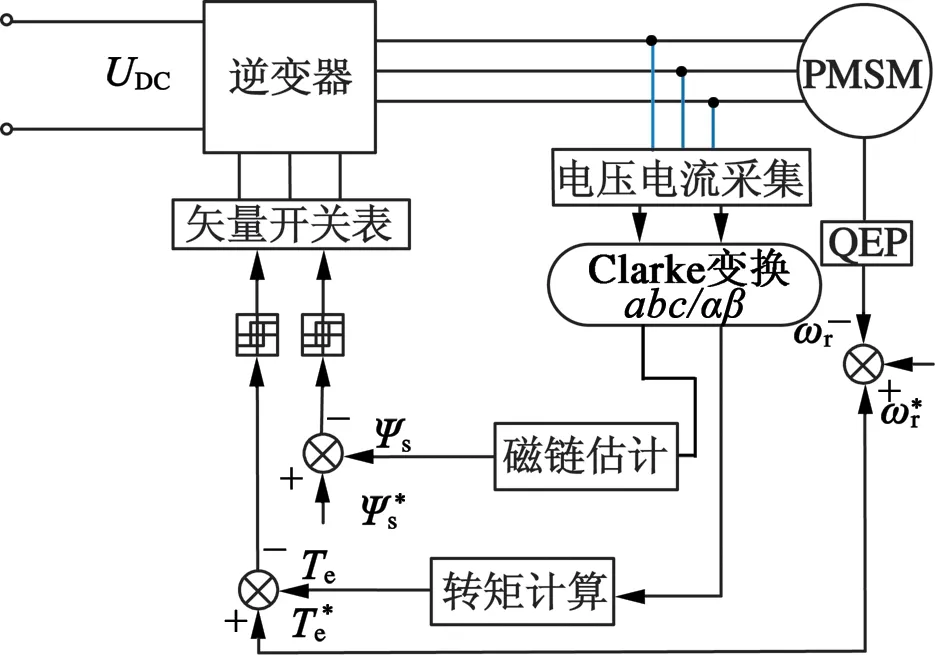
圖1 傳統DTC控制框圖

PMSM傳統DTC控制方案是基于α-β靜止坐標系下由感應電機控制策略推廣而來。通過檢測電機定子電壓電流，計算出電機的定子磁鏈幅值、角度和轉矩。將計算值分別與給定值進行滯環比較，根據磁鏈位置和轉矩控制信號選擇合適的電壓矢量。轉速誤差經過PI調節器后得到轉矩給定，而磁鏈的給定則由不同的控制目標分別采取不同的控制算法。如最大轉矩電流比控制、恒定子磁鏈控制等。估計后的磁鏈要進行扇區判斷，就需要得到磁鏈角度。磁鏈幅值和磁鏈角度可由下式求得：

(4)

(5)

可以看出，以磁鏈為控制目標的控制方式由于磁鏈的積分和反三角函數計算，導致計算量較大，并且由于積分運算，容易受采樣誤差影響。

2 無磁鏈觀測DTC方案

2.1 轉矩控制原理

PMSM運行矢量如圖2所示。

圖2中，ψf,ψs分別為永磁體磁鏈和定子磁鏈;is為定子電流;δ為定子磁鏈與d軸夾角;θ為d軸與a相軸線夾角。

由于表貼式PMSM交直軸氣隙相差很小，因此，可令Ld=Lq。結合式(2)，PMSM電磁轉矩可以表示：

(6)

式中：ψq為電機q軸磁鏈。

此時，從式(6)可以看出，除了負載角δ，還存在變量ψs。在一定范圍內，負載轉矩隨著磁鏈幅值和負載角正弦值的增加而增加。用一個電壓矢量同時實現兩個變量的最優控制，計算比較復雜。對于PMSM，定子磁鏈ψf由永磁體直接產生，是一個恒定值。因此，對電機轉矩進行關于ψq的微分運算，得到下式：

(7)

當忽略定子電阻壓降時，有：

(8)

因此，可以通過控制q軸電壓分量變化最大達到PMSM電磁轉矩變化最快的目的。這就意味著若使逆變器選擇q軸分量較大的電壓矢量作用于電機，達到電磁轉矩快速變化的目的。此時，轉矩環可通過對交軸電壓uq的直接控制實現，對轉矩的控制也從定子磁鏈的轉矩角轉移到電壓矢量的交軸分量上來。

但以此作為開關表確定依據，有可能造成定子磁鏈幅值過大，使定子繞組磁鏈飽和，最終電機無法穩定運行，因此需要對磁鏈進行控制。

2.2 電流限制

結合矢量控制理論，表貼式PMSMid=0控制算法簡單，易于實現，能同時實現最大轉矩電流比控制，被廣為采用[12]。傳統DTC的id=0控制策略利用直軸電流id與磁鏈幅值的一一對應的特點，在一個控制周期內，轉矩已知，利用式(9)計算出磁鏈幅值的給定，進而到id=0的控制效果。借鑒這個思路，如果對直軸電流id進行控制，那么在某個已知轉矩下，就一定有與之對應的定子磁鏈幅值，因此就不需要對磁鏈幅值進行限制。其次，由于定子磁鏈是一個矢量，如果以電流環替換磁鏈環，將導致磁鏈角或者負載角δ的缺失。基于PMSM的位置傳感器特點，采用定子磁鏈角度θ經過計算代替負載角δ。

(9)

由式(1)中電壓模型可知，id與直軸電壓ud密切相關。忽略定子電阻，電機穩態運行時有：

(10)

因此，通過ud可以達到快速控制電流id的目的，并且，電流變化會隨著直流母線電壓的增加而增大。因此，母線電壓要合理選擇，過高則脈動較大，控制周期變小;過低則電機運行不穩定，控制響應變慢。

圖3為三相兩電平逆變器電壓矢量圖。圖3中θ為轉子與定子繞組A相軸線的夾角，d軸正方向為永磁體磁鏈方向。圖4為空間電壓矢量隨轉子位置變化規律。以轉子磁鏈位置為參考，將空間電壓矢量等分為6個扇區，以ud，uq為控制目標，以轉矩響應為優先選擇對象，重新選擇開關表。

圖3 電壓矢量圖

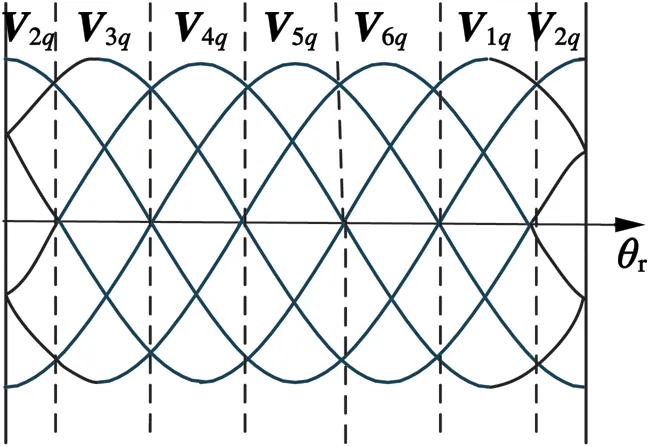
圖4 空間電壓矢量隨轉子磁鏈位置θr變化規律

圖5為定子電流與電壓矢量關系圖。圖5中，ΔTs為電壓矢量作用時間，is(n)為電壓矢量作用后下一個時刻定子電流狀態。

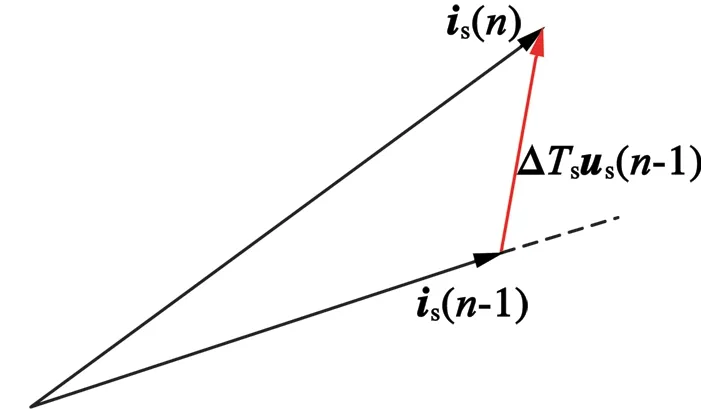
圖5 定子電流和電壓矢量關系圖

基于無磁鏈觀測的PMSM DTC控制框圖如圖6所示。轉矩給定由轉速差經過速度調節器得到，將轉矩給定T*與實際轉矩進行滯環比較輸出轉矩控制信號。將原本的磁鏈控制環由d-q坐標下的電流環來代替，新的優選矢量開關表代替傳統開關表，輸出的開關信號由轉矩控制信號τ，電流控制信號以及位置傳感器的位置信號得到。

圖6 基于無磁鏈觀測的DTC控制框圖

3 仿真驗證

為驗證控制方案的正確性和有效性，進行了仿真分析。以一臺額定功率為150 kW的表貼式PMSM為研究對象，具體參數：額定轉速為23.8 r/min，定子電阻為0.8 Ω，d,q軸電感為23 mH，電機極對數為30對極，永磁體磁鏈為7.144 Wb。仿真時給定轉矩為50 000 N·m，轉速為10 r/min，t=0.5 s時轉速突變為23.8 r/min。

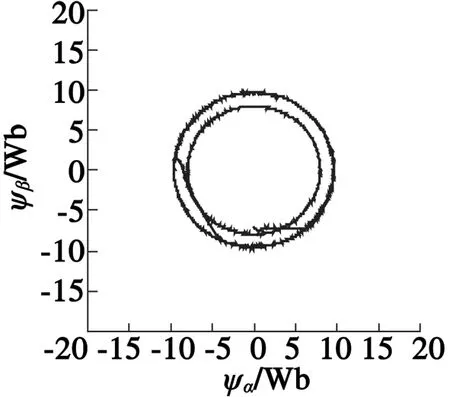
(a) 定子磁鏈軌跡

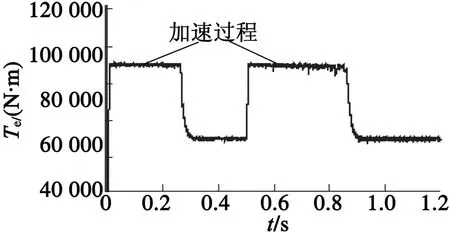
(b) 電磁轉矩

圖7定子磁鏈和轉矩仿真波形

圖7分別為定子磁鏈軌跡和電磁轉矩波形。可以看出，磁鏈幅值得到了很好的控制，軌跡為圓形，其中，磁鏈幅值變大的過程為轉矩增大的過程，到達轉矩限幅后，磁鏈幅值維持在可控范圍之內。雖然采用有差的滯環控制，但磁鏈軌跡相對平滑，說明上述方案能實現對定子磁鏈的控制。從圖7(b)的電磁轉矩波形看出，轉矩有較快響應，因為選擇矢量依據轉矩響應優先的原則選取。穩態轉矩脈動在4%左右，比傳統DTC有所下降。其次，由于是電機轉矩直接響應電壓矢量的變化，因此，輸出電磁轉矩對給定轉矩的相應較快，其中直流側母線電壓的大小會影響轉矩波動情況，并且在大轉矩下轉矩脈動效果抑制更明顯。

電機轉矩階躍響應如圖8所示。可以看出，在負載轉矩突變時，電機能快速跟蹤負載轉矩變化做出調節，并且沒有過大的超調，達到了理想的控制效果。

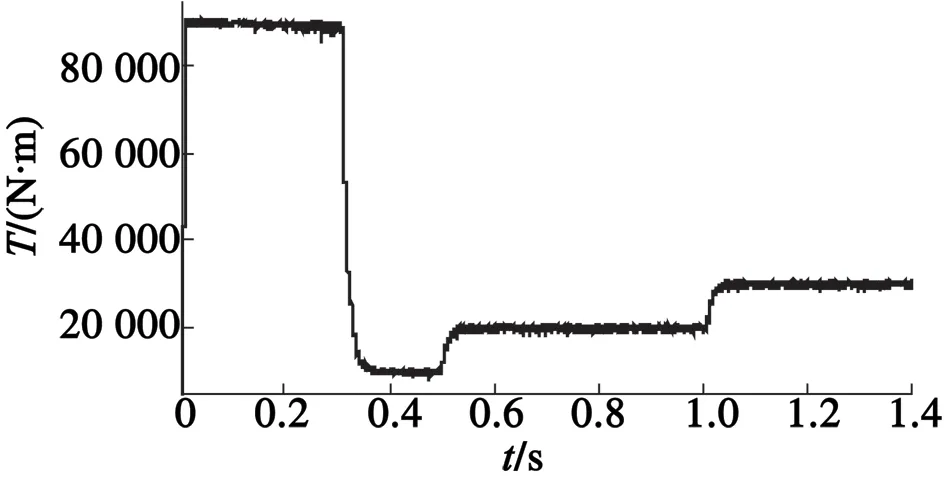
圖8 電磁轉矩階躍響應波形

圖9為三相PMSM定子電流。可以看出，在0.3s和0.9 s分別達到穩態。在0.5 s時轉速突變時，能較快響應指令。并且定子電流脈動較小，正弦畸變較小，達到勻速后電流下降相對平滑。說明所選的電壓矢量在不進行磁鏈估計和限幅的情況下，仍能對電流進行控制，同時達到間接的磁鏈控制效果。

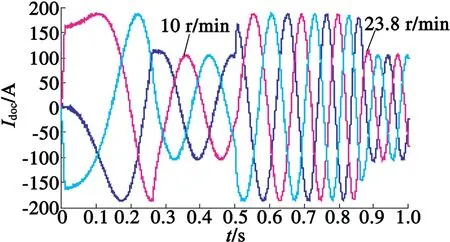
圖9 三相定子電流仿真波形

4 結 語

針對傳統的DTC磁鏈估計計算復雜，計算量較大，電流控制效果不理想等問題，提出了基于定子磁鏈角為基準劃分扇區，增加直軸電流id控制環的控制方案。在電壓矢量的選擇中，將電壓矢量分解到旋轉坐標d,q分量，并基于轉矩響應最優的原則選取電壓矢量。該方案不需要對磁鏈的實時計算，同時達到了轉矩的快速響應和定子電流畸變小的控制特性。最后，通過仿真驗證了該方案的正確性和有效性。

[1] 楊影,陳鑫,涂小衛,等.占空比調制的永磁同步電機直接轉矩控制[J].電機與控制學報,2014,18(4):66-71.

[2] 李耀華,馬建,劉晶郁,等.電動汽車用永磁同步電機直接轉矩控制電壓矢量選擇策略[J].電機與控制學報,2012,16(4):43-49.

[3] TAKAHASHI I,NOGUCHI T.A new quick-response and high-efficiency control strategy of an induction motor[J].IEEE Transactions on Industry Applications,1986,22(5):820-7.

[4] 陳振,劉向東,廖曉鐘,等.基于十二扇區細分的永磁同步電動機直接轉矩控制[J].微特電機,2011,39(5):42-6.

[5] MATHAPATI S,BOCKER J.Analytical and offline approach to select optimal hysteresis bands of DTC for PMSM[J].IEEE Transactions on Industry Electronics,2013,60(3):885-95.

[6] 曹林柏,趙宏革,張智遠,等.一種永磁同步電動機直接轉矩控制策略研究[J].微特電機,2016,44(4):47-51.

[7] 李光葉,萬健如,劉英培,等.基于模糊零矢量永磁同步電機直接轉矩控制[J].電力自動化設備,2009,29(9):31-5.

[8] XIA C,WANG S,GU X,et al.Direct torque control for VSI-PMSM using vector evaluation factor table[J].IEEE Transactions on Industry Electronics,2016,63(7):4571-83.

[9] 陳煒,艾士超,谷鑫.基于最小電壓矢量偏差的永磁同步電機直接轉矩控制[J].電工技術學報,2015,30(14):116-21.

[10] 王斌,王躍,王兆安.空間矢量調制的永磁同步電機直接轉矩控制[J].電機與控制學報，2010,14(6):45-50.

[11] FAIZ J,MOHSENI-ZONOOZI S H.A novel technique for estimation and control of stator flux of a salient-pole PMSM in DTC method based on MTPF[J].IEEE Transactions on Industry Electronics,2003,50(2):262-71.

[12] 李耀華,劉衛國.永磁同步電動機直接轉矩控制系統的最大轉矩電流比控制[J].微特電機，2007,35(1):23-6.