基于擾動補償的PMSM轉速環自抗擾控制器設計
謝傳林,曾岳南,王發良,曾祥彩
(廣東工業大學,廣州 510006)
0 引 言
自抗擾控制器(以下簡稱ADRC)作為應用于永磁同步電機(以下簡稱PMSM)控制中的一種非線性算法,能夠對系統的內、外擾動進行估計并給予補償,不依賴于對象模型[1]。擴張狀態觀測器(以下簡稱ESO)作為ADRC的核心部分,其觀測精度越高,系統的控制性能越好。然而在系統實際運行中,ESO所估計的擾動量較多且變化幅度很大,使得ESO難以保證對擾動有較高的估計精度,導致擾動不能夠完全補償,影響了ADRC的控制性能。為此,國內外學者進行了大量的研究,文獻[2]提出了基于負載觀測的自抗擾控制器設計,但是擾動補償范圍較小。文獻[3]提出了基于滑模控制的模型補償自抗擾控制器設計,利用辨識算法估計出轉動慣量和負載轉矩,從而減輕了ESO的觀測負擔,但由于滑模控制開關的切換動作所造成的控制不連續性,抖振現象無法避免。
針對上述問題,本文設計了基于擾動補償的ADRC。首先通過參數辨識的方法估計出轉動慣量和負載轉矩,把部分擾動項表示出來并補償到ADRC的擾動觀測輸出中,減小ESO的觀測負擔,提高ESO對擾動量的觀測精度,進而增加轉速環抗擾性能。最后根據基于帶寬的參數整定方法得到控制器參數,通過仿真和實驗表明,轉速環采用基于擾動補償的ADRC與采用線性ADRC相比,抗擾性能更優越。
1 PMSM數學模型
對于表貼式PMSM在d-q旋轉坐標系下的電壓和磁鏈方程可以表示:
(1)
(2)
電磁轉矩和運動方程:
(3)
(4)
式中:ud,uq分別為定子d,q軸電壓;id,iq分別為定子d,q軸電流;L為定子電感;ψd,ψq分別為定子磁鏈d,q軸分量;ψf為轉子磁鏈;ω為轉子電角速度;ωr為轉子機械角速度;Rs為定子電阻;p為電機的極對數;Te為電機的電磁轉矩;TL為電機負載轉矩;J為轉動慣量;B為電機的摩擦系數。
2 轉速環控制器的設計
2.1 基于擾動補償的自抗擾控制器設計
線性自抗擾控制器(以下簡稱LADRC)具有參數整定方便、算法簡單等優點,它包括線性跟蹤微分器(以下簡稱LTD)、線性擴張狀態觀測器(以下簡稱LESO)以及線性狀態誤差反饋(以下簡稱LSEF)3個部分[4]。根據式(4)可知,轉速輸出為一階微分方程,因此選取一階LADRC作為轉速環控制器[4]。通過轉動慣量辨識和負載轉矩觀測得到部分擾動項,并將補償到ADRC擾動估計輸出項中,同時與LSEF對總擾動的補償一起組成控制量,實現轉速反饋對轉速給定的跟隨。
由式(3)、式(4)可得:
(5)

(6)
式中:b0為可變參數。可得:
(7)
式中:fω為總擾動量。令x1=ω,x2=fω,u=iq,式(6)可寫為:
(8)
為了LESO設計方便,將式(8)寫為:

(9)

為了得到擾動量的數值,由式(9)設計的LESO的方程:
(10)
式中:β1,β2表示LESO的增益;z1,z2表示狀態量的觀測值;x1表示狀態量的實際值。

(11)
通過擾動補償后,轉速開環可由一個積分環節來表示。因此,選取比例控制作為控制律,即:
(12)

(13)


圖1 轉速環采用基于擾動補償ADRC結構圖
2.2 轉動慣量的辨識
由于采樣時間很小,可以得出:
(14)
式中:Ts為采樣周期。
將式(14)代入到式(7)中,可得:
ωr(k)=ωr(k-1)+(Ts/J)·
[Te(k-1)-TL(k-1)]
(15)
由于機械負載轉矩在兩個采樣時間內變化很小,可以看作恒定,因此對于式(15)中的負載轉矩有:
TL(k)=TL(k-1)
(16)
由式(15)可得:
ωr(k-1)=ωr(k-2)+(Ts/J)·
[Te(k-2)-TL(k-2)]
(17)
聯立式(15)、式(17)可得:
ωr(k)=2ωr(k-1)-ωr(k-2)+
b(k-1)U(k-1)
(18)
式中:U(k-1)=Te(k-1)-Te(k-2);b(k-1)=Ts/J。
將式(18)作為轉動慣量辨識的參考模型,即:

(19)
利用梯度校正估計算法[5-6],可得:
(20)
由式(20)可以得到轉動慣量的估計值:
(21)
2.3 負載轉矩觀測器的設計
由式(5)得:
(22)
由于負載轉矩不易直接測量,可以通過已獲得的iq,ω來觀測。由于測量iq和ω時會有噪聲誤差的存在,使測量值不準確,因此為了得到精確的測量值,在負載轉矩觀測器的輸出端加入一階低通濾波器[7],加入濾波器后式(22)變為:
(23)
式中:T1為一階低通濾波器的時間常數。
將式(23)進行拉氏變換并整理可得:
(24)

對A取拉氏反變換可得:
(25)
聯立式(24)及式(25)可得:
(26)
3 仿 真
在MATLAB/Simulink平臺上搭建轉速環,采用基于擾動補償的ADRC雙閉環調速系統仿真模型,電機參數如表1所示,并和轉速環采用LADRC的控制效果進行對比,其參數整定是基于轉速環帶寬指標[8],如表2所示。轉速環參數可按表2給出的計算方法得到,其中:ωcv,ω0以及b0分別為200,1 000以及50。電流環均采用PI控制器,PI參數由工程整定方法可得[9]。

表1 伺服電機參數

表2 轉速環一階LADRC整定公式
表2中ωcv為轉速閉環帶寬;ω0為觀測器帶寬,取ω0=5ωcv~10ωcv;τ為LTD的慣性時間常數。
當轉速給定1 000r/min,在0.5s時突加50%額定負載時,采用LADRC和基于擾動補償的ADRC控制的系統轉速響應如圖2所示,觀測器對擾動的跟蹤波形如圖3所示,系統總擾動量如圖4所示。由圖2、圖3可知,采用基于擾動補償的ADRC控制的系統在突加負載后,可以更快地恢復到穩態,轉速跌落更小。而采用LADRC控制的系統在突加負載后,轉速恢復時間更長,轉速跌落也更大。

圖2 突加負載時轉速響應曲線

圖3 擾動觀測值對比
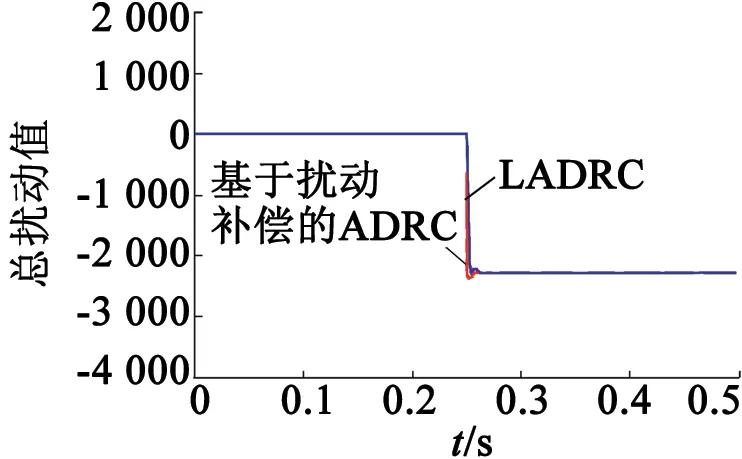
圖4 總擾動對比
4 實 驗
上述理論通過實驗驗證其有效性,實驗中的參數設置條件與仿真參數相同。實驗平臺如圖5所示。

圖5 加載實驗平臺
抗負載擾動性能實驗:轉速給定為1 000r/min,轉速達穩態后突加50%額定負載,采用LADRC和基于擾動補償的ADRC控制的系統的轉速跌落如圖6所示,由圖6可知,在負載轉矩擾動作用下,采用基于擾動補償的ADRC控制的系統抗負載擾動效果優于采用LADRC控制的系統。

(a) 采用LADRC轉速響應波形
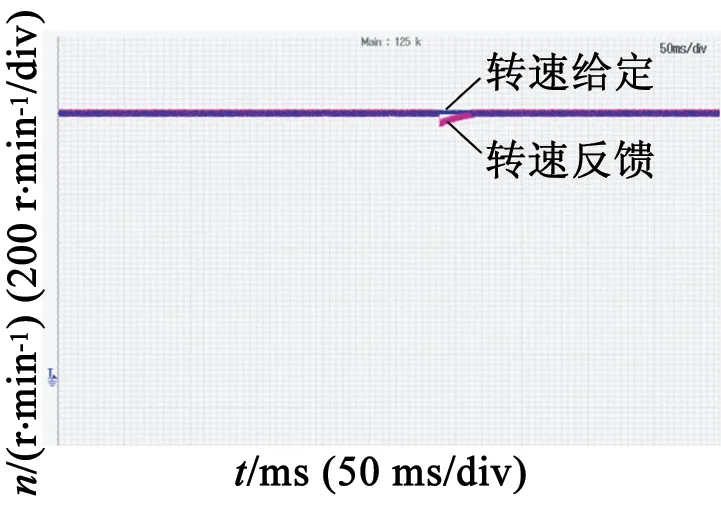
(b) 采用基于擾動補償的ADRC
5 結 語
本文在線性自抗擾控制技術的基礎上,辨識了負載轉矩以及轉動慣量,設計了基于擾動補償的ADRC,并將其應用于PMSM轉速環控制。仿真和實驗表明,基于擾動補償的ADRC有效減小了觀測器的觀測負擔,提高了擾動估計精度,具有更好的抗負載擾動能力,有效抑制負載變化對轉速的影響。
[1]HANJQ.FromPIDtoactivedisturbancerejectioncontrol[J].IEEETransactionsonIndustrialElectronics,2009,56(3):900-906.
[2] 蓋江濤,黃守道.基于負載觀測的永磁電機驅動系統自抗擾控制[J].電工技術學報,2016,31(18):29-36.
[3]CHENHJ,XUH,LIUB,etal.ThecompensatedactivedisturbancerejectioncontrollerbasedonslidingmodecontrolforPMSM[C]//The5thAnnualIEEEInternationalConferenceonCyberTechnology,2015:240-245.
[4] 曾岳南,曾祥彩.永磁同步電機調速系統自抗擾控制器的設計[J].電氣傳動,2017(4):3-6.
[5] 沈艷霞,劉永欽.基于改進型模型參考自適應的PMSM參數辨識[J].電氣傳動,2009,39(5):47-50.
[6] 章瑋,王偉穎.基于降階負載擾動觀測器的永磁同步電機控制[J].機電工程,2012,39(7):821-832.
[7] 劉志剛,李世華.基于永磁同步電機模型辨識與補償的自抗擾控制器[J].中國電機工程學報,2008,28(24):118-123.
[8]GAOZQ.Scalingandbandwidth-parameterizationbasedcontrollertuning[C]//ProceedingsoftheAmericanControlConference.Denver:IEEE,2003:4989-4996.
[9] 阮毅,陳伯時.電力拖動自動控制系統-運動控制系統[M].4版.北京:機械工業出版社,2012.

